Grundpfeiler des Kraftsports - 2b1 Performance

Kompensationsstrategien; wie man Schwachpunkte einer Bewegung erkennt

Bis zu diesem Punkt wurden im Kontext der Biomechanik Thematiken von den physikalischen Hintergründen zu Kraft und Drehmomenten, über die biomechanischen Prinzipien des Bewegungsapparates und der Funktionsweise der Skelettmuskulatur, bis hin zu einer biomechanischen Betrachtung des Bewegungsapparates in Bewegung und Training, einschließlich der mechanischen Funktionsweise von Trainingsmaschinen und dessen Auswirkung auf den Menschen besprochen. Der vorliegende Abschnitt soll nun gewissermaßen daran angeknüpft, oder besser gesagt, darauf aufbauen. Und zwar geht es genauer gesagt darum, ausgehend einer jeweiligen Bewegung und den wirkenden Kräften nicht nur grob auf die muskuläre Belastung im Laufe der Bewegung zu schließen, sondern ausgehend hiervon ebenso die anspruchsvollsten Positionen ebenso wie eventuelle Schwachpunkte in einer Bewegung zu identifizieren. Mit Schwachpunkten sind hier vor allem muskuläre Schwächen bei mehrgelenkigen Bewegungen mit einer Reihe beteiligter Muskeln und Muskelgruppen gemeint. Aber auch abseits davon soll es im Wesentlichen darum gehen, Bewegungen aus (bio)mechanischer Sicht besser lesen zu können. Zugutekommt uns dabei die mechanische Verbindung von Kraft und Bewegung. Holen wir hierzu aber nochmals etwas aus, indem wir auf einige vorherige Thematiken zurückgreifen.

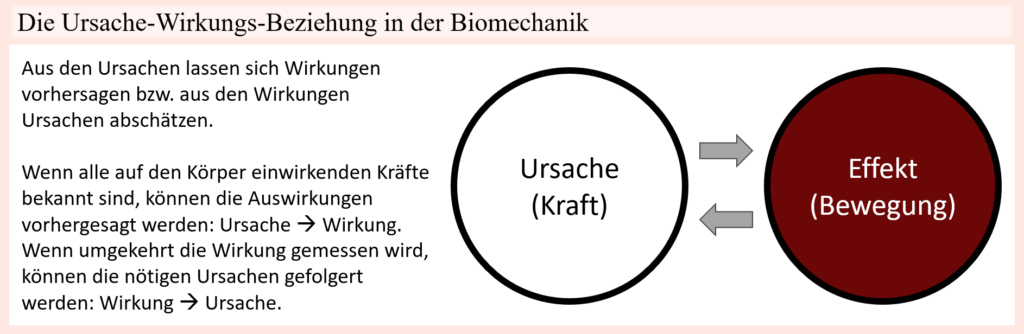
Wie in Newtons erstem Gesetz schön beschrieben wird, behält ein kräftefreier Körper seinen Bewegungszustand bei. Im Vakuum könnte dieser Bewegungszustand nun entweder die Ruhe als auch eine gleichmäßige, geradlinige Bewegung sein. Das bedeutet, ein kräftefreier, sich bewegender Körper bleibt auch in Bewegung und ein kräftefreier ruhender Körper bleibt in Ruhe. Dadurch dass wir uns aber nicht in einem Vakuum befinden, und für uns im Alltag jegliche Bewegung auch mit Reibung einhergeht, welche jede Bewegung abbremst, kommen gleichmäßig, geradlinige, kräftefreie Bewegungen, die unendlich fortschreiten, nicht vor. Das zweite Newtonsche Gesetz setzt weiterhin die Masse eines Körpers in Verbindung mit den wirkenden Kräften und der resultierenden Beschleunigung. Daraus folgt eine Definition für den Kraftbegriff, welche besagt, dass Kraft die Ursache für eine Beschleunigung (bzw. im praktischen Sinne für eine Bewegung) ist. Diese „Beschleunigung“ verstehen wir als Bewegungsänderung, sei es ein schneller werden, langsamer werden oder auch ein Verformen, wobei analog für Drehbewegungen das Gleiche gilt, nur dass der Begriff Kraft eben durch das Drehmoment ersetzt wird (was gewissermaßen als „Drehkraft“ zu verstehen ist). Übertragen auf den Bewegungsapparat schließen wir daraus, dass auch dessen Bewegungen die Folge wirkender Kräfte sind. Diese Kräfte können einerseits natürlich von außen einwirken, andererseits aber eben auch körperintern von Muskeln erzeugt werden. Resultierende Bewegungen entsprechen dabei gleich der Summe aller einwirkenden Kräfte. Dank dieser direkten Verbindung von Kraft und Bewegung können wir ausgehend der von außen auf den Bewegungsapparat einwirkenden Kräften sowie den resultierenden Gelenkbewegungen auf die muskuläre Komponente schließen, weil wir durch das anatomische Hintergrundwissen, was das Skelettmuskelsystem betrifft, den einzelnen Muskeln bzw. Muskelgruppen Bewegungsfunktionen zuweisen können. So ziehen bestimmte Muskeln gemäß ihrem anatomischen Verlauf über gewisse Gelenke und können durch ihre Kontraktion Drehmomente in entsprechenden Gelenken erzeugen, welche wiederum bestimmte Bewegungen verursachen können. Sind also die von extern einwirkenden Kräfte, samt deren Auswirkung auf belastete Gelenke, ebenso wie die letztendliche Bewegung bekannt, dann lässt sich schlussfolgern, welche Muskeln Kraft erzeugt haben müssen (und in welchem groben Ausmaß), damit jeweilige Bewegung resultieren konnte. Beläuft sich entsprechende Bewegung bzw. Belastung nur auf ein einzelnes Gelenk, dann ist dies besonders einfach, aber auch wenn mehrere Gelenke beteiligt sind, bleibt das Prinzip gleich, weil auch hier einzelne Muskeln für bestimmte Gelenke bzw. bestimmte Bewegungen zuständig sind, sodass eine komplexere Bewegung dementsprechend heruntergebrochen werden kann, indem die Bewegung und Belastung der jeweils beteiligten Gelenke betrachtet wird und von dort aus auf zuständige Muskulatur geschlossen wird. Wohlgemerkt bewegen wir uns hier in einem Rahmen, in welchem es vielmehr um möglichst gutes Abschätzen und weniger um exaktes Nachvollziehen geht, denn dies wäre nicht oder nur mit sehr viel Aufwand und selbst dann nur teilweise möglich. Dies gilt besonders für Bewegungen, welche in geschlossenen kinematischen Ketten ablaufen. Glücklicherweise ist es aber nicht notwendig, die Belastung des Körpers und Krafterzeugung einzelner Muskeln genau in Zahlen auszudrücken. Vielmehr reicht eine möglichst gute Annäherung, um die wichtigsten Erkenntnisse daraus zu gewinnen, die dazu genutzt werden können, um die Anforderungen und Beteiligung von Muskeln im Laufe einer Bewegung, samt eventueller Schwächen zu identifizieren, die wiederum dazu genutzt werden können, um sportliches Training zielgerecht zu gestalten.

Um in realen Situationen aber überhaupt in der Lage zu sein, die mechanischen Begebenheiten von Bewegungen auch nur näherungsweise bestimmen zu können, müssen teilweise gewisse Hilfsmittel mit an die Hand genommen werden. Die Schwierigkeit natürliche Bewegungen von Lebewesen mechanisch nachzuvollziehen, ist ein grundlegendes Problem, mit welchem die Biomechanik seit je her kämpfen muss. So beschäftigte man sich bereits in der Antike mit der Bewegung von Tieren und wollte nachvollziehen, wie diese Bewegung funktioniert.

So fragten sich zum Beispiel bereits die alten Ägypter, ob ein galoppierendes Pferd im Laufe dieser Bewegung jemals alle Hufe vom Boden abhebt. Was auf den ersten Blick als banale, oder zumindest einfach zu überprüfende Frage erscheint, indem man sich einfach ein galoppierendes Pferd ansieht, erwies sich aber als Problem, das erst lange Zeit später, in der Moderne gelöst werden sollte. Auch Aristoteles, der Hunderte von Jahren vor Christus ein ganzes Werk, „De Motu Animalium“, über die Fortbewegung von Tieren schrieb, war noch nicht in der Lage, die Kinematik der Bewegung von Tieren und der Frage, ob ein galoppierendes Pferd jemals alle Hufe vom Boden abhebt, empirisch zu belegen. Grund hierfür war, dass Aristoteles und die alten Ägypter auf ihre visuelle Beobachtung angewiesen waren und die Bewegungsabläufe von Tieren, darunter auch ein galoppierendes Pferd, sich zu schnell bewegten, als dass man diese Bewegung mit bloßem Auge klar nachverfolgen könnte. Erst im späten 19. Jahrhundert kam Licht ins Dunkle, als der Eisenbahn-Unternehmer Leland Stanford den Fotografen Eadweard Muybridge dazu beauftragte, der Frage auf den Grund zu gehen, ob ein galoppierendes Pferd nun immer mindestens einen Huf am Boden hat oder ob sich kurzzeitig alle vier Hufe in der Luft befinden. Daraus entstand Muybridges simpler, aber doch genialer Versuchsaufbau, der einen Meilenstein für die Welt der Biomechanik bedeuten sollte. Das galoppierende Pferd lief dabei an einer weißen Wand entlang. Gegenüber dieser Wand waren zwölf bzw. 24 Kameras in einer Reihe aufgestellt, deren Auslöser jeweils mit einem feinen Draht verbunden war, welche quer über die Rennbahn gezogen waren. Das Zerreißen des Drahts durch das galoppierende Pferd bewirkte mittels eines elektrischen Impulses die Auslösung der jeweiligen Kamera. Das Resultat war eine Bildserie, welche die Bewegung des galoppierenden Pferdes festhielt. Wo man früher mit bloßem Auge nicht hinterherkam, den Bewegungsablauf nachzuverfolgen, hatte man jetzt Bilder. Die schnelle und fließende Bewegung wurde auf einzelne Frames (Einzelbilder) heruntergebrochen und konnten in Ruhe begutachtete werden. Und siehe da, auf einigen Frames sieht man ganz klar, dass sich alle Hufe in der Luft befinden.

Auch wenn wir uns in diesem Kontext natürlich nicht speziell für die Kinematik der Bewegung von Pferden interessieren, ist dies ein Vorzeigebeispiel dafür, warum der technische Fortschritt und die dadurch ermöglichte Erweiterung des menschlichen Erkenntnisvermögens ein Grundbaustein der Naturwissenschaften ist.

Durch den Einsatz der verfügbaren Kameratechnik konnten auch die Bewegungen des Menschen ersichtlicher gemacht werden, sodass immer mehr Einblick in die Koordination der Gliedmaßen möglich war. Zunächst beschränkte sich dies natürlich auf relativ simple Methoden der Serienfotografie, jedoch schritt die Biomechanik mitsamt der Verfügbarkeit neuer Technologien schnell voran. Kameras wurden von Tag zu Tag weiterentwickelt und heutzutage sind Computer sogar in der Lage, Berechnungen durchzuführen, gleichzeitig Bewegungen zu erkennen und das alles als dreidimensionale Modelle wiederzugeben. All dies ermöglicht es, kinematische und auch kinetische Begebenheiten verschiedenster Bewegungsabläufe immer besser erkenntlich zu machen.

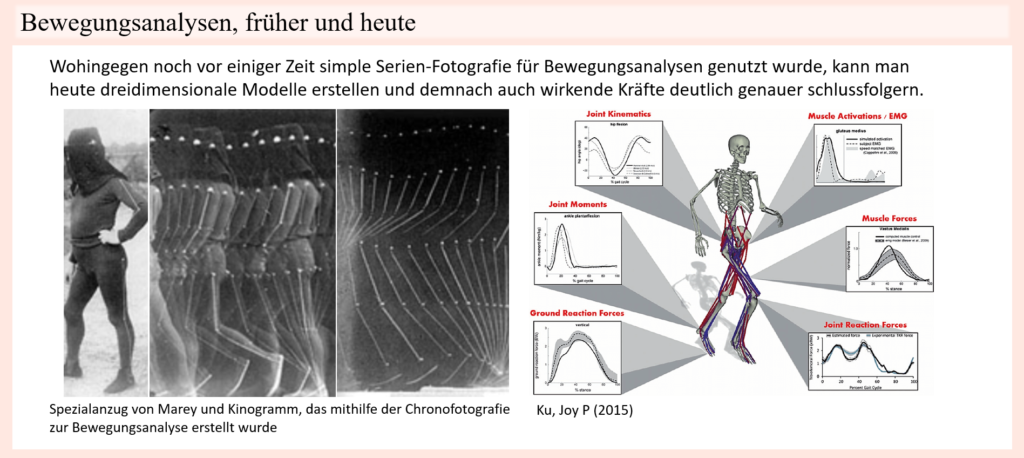
Wohlgemerkt ist man in alltäglichen Situationen nicht dazu in der Lage, solch komplexe Analysen durchzuführen, wenn man bedenkt, dass dahinter noch großer Aufwand steckt, der neben einer entsprechenden Software und der Datenauswertung zum Beispiel Infrarotkameras, Reflexionsmarkern, EMG-Aufzeichnung und Druckmessplatten mit einschließt. Aus diesem Grund finden hochmoderne Bewegungsanalyse-Methoden bis dato auch hauptsächlich in Forschungszwecken und Therapie und nicht zum Beispiel im alltäglichen Training von Sportlern Verwendung. Trotzdem sind natürlich gerade hier Bewegungsanalysen wichtig. Schließlich besteht ein wesentlicher Fokus sehr vieler Sportarten darin, dieentsprechenden, in der Sportart vorkommenden, Bewegungen zu optimieren. Und dies basiert eben genau darauf, durch gewisse Formen der Analyse Schwachpunkte der Bewegung zu identifizieren und diese dann durch gezieltes Training aufzuarbeiten. Klassischerweise fällt gerade dies in den Aufgabenbereich erfahrener Trainer, die durch ihr geschultes Auge und ihre Praxiserfahrung verstehen, Bewegungen zu lesen und ausgehend davon zu schlussfolgern, wovon ein jeweiliger Athlet profitieren würde. Doch auch noch so erfahrenen Trainern kommen kleine technische Hilfsmittel zur Erweiterung ihres Erkenntnishorizontes zugute, um Dinge zu sehen, die man ansonsten nicht, oder nur schwer sehen könnte. Das Festhalten von Bewegungen im Videoformat ist dabei ein grundlegendes Hilfsmittel, welches durch den geringen Aufwand und die Tatsache, dass die meisten Menschen jederzeit eine Kamera in Form eines Smartphones griffbereit haben, die bequeme Möglichkeit schafft, eine Bewegung, welche einige Sekunden dauert, festzuhalten, sodass diese beliebig oft, in unterschiedlicher Geschwindigkeit und sogar Frame für Frame begutachtet werden kann. So wie Muybridge zu seiner Zeit bereits durch die Serienfotografie Bewegungen mit einer Reihe von Einzelbildern festhielt, kann dies heute ganz unproblematisch, mit kaum Aufwand und in deutlich höherem Ausmaß gemacht werden. Wir müssen dazu nicht einzelne Kameras in einem großen Versuchsaufbau aufstellen und diese nacheinander auslösen, sondern können mit einer ganz regulären Kamera bereits 24 oder mehr Bilder pro Sekunde aufnehmen. Im Kontext der Biomechanik bzw. einer biomechanischen Betrachtung einer Bewegung und der weiter oben angesprochenen Verbindung von Kräften (bzw. Drehmomenten) und Bewegung, auf denen dies alles basiert, sind solche Momentaufnahmen deswegen von Vorteil, weil hierdurch auch kleinste Bewegungsänderungen und damit Kraft- bzw. Lastverschiebungen besser ersichtlich gemacht werden können. Auch im vorliegenden Abschnitt werden wir weiter unten einzelne Frames aus Videos zur Hand nehmen, um vor allem solche Last-Verschiebungen deutlicher aufzuzeigen. Hinzu kommt, dass wir heutzutage auch nicht mehr zwangsweise daran gebunden sind, Fotos und Videos mit bloßem Auge zu betrachten, denn auch dies kann etwas unübersichtlich werden, wenn es um kleine Bewegungen geht. So wäre es mit Muybridges Serienfotografie natürlich schwergefallen, festzustellen, inwieweit das Bewegungsmuster des galoppierenden Pferdes konsistent ist, bzw. wie groß die Varianz dabei ausfällt. Glücklicherweise stehen uns heute aber technische Hilfsmittel in Form von Software zur Verfügung, welche, richtig eingesetzt, das Ganze deutlich einfacher machen kann, zum Beispiel, indem bewegte Objekte nachverfolgt werden. Auf diese Weise können zum Beispiel Gelenkwinkel gemessen, Markerpunkte gesetzt, nachverfolgt und Bewegungsgeschwindigkeiten angezeigt werden. Wie wir weiter unten sehen werden, denn dort sind in einigen der dargestellten Frames eben solche Markerpunkte verwendet worden, machen es solche Hilfsmittel bedeutend einfacher Bewegungspfade nachzuvollziehen.

Im vorliegenden Abschnitt werden einzelne Frames solcher Videoaufnahmen mit Bewegungsverfolgung vor allem im Kontext klassischer Trainingsübungen aus dem Kraftsport, genauer gesagt Kniebeugen, Kreuzheben und Bankdrücken Verwendung finden, um Lastverschiebungen in diesen Bewegungen deutlicher zu machen, jedoch gehen die Anwendungszwecke natürlich weit darüber hinaus. Hier geht es dabei vor allem darum aufzuzeigen, wie die jeweiligen muskulären Schwächen und Stärken entsprechender Bewegungen ausgehend solcher Analysen und dabei beobachteten Kompensationsbewegungen identifiziert werden können. Was Kompensationsbewegungen sind und inwiefern man eben durch solche die mechanischen Begebenheiten sowie eventuelle Stärken und Schwächen eines Trainierenden ablesen kann, dazu später. Bevor wir nämlich dazu kommen, geht es im Folgenden um ein anderes, aber gewissermaßen damit in Verbindung stehendes Thema, welches man umgangssprachlich durch die englische Bezeichnung „sticking points“ kennt.

Sticking Points

„Sticking Points“ sind ein Konzept, das häufig im Zusammenhang mit Widerstandstraining aufgegriffen wird. Im Wesentlichen bezieht es sich auf den Teil eines Bewegungsbereichs, bei dem die Schwierigkeit, die Bewegung fortzusetzen, verhältnismäßig stark zunimmt. Wird die Bewegung dabei bis zur Erschöpfung ausgeführt, kommt es im Bereich solcher Sticking Points dementsprechend auch zum Übungsversagen.

Solch eine grobe Beschreibung dafür, was Sticking Points sind, findet man recht häufig, schließlich ist diese ja auch relativ intuitiv. Wenn es aber um eine genaue Definition samt einer daraus resultierenden Folgerung, wo sich Sticking Points bei jeweiligen Bewegungen befinden, dann stellt sich heraus, dass dies tatsächlich erstaunlich schwer zu sein scheint. Bevor wir aber zu einigen vorgeschlagenen Definitionen und wichtigen Aspekten diesbezüglich kommen, steht natürlich erst einmal die Frage im Raum, welchen Vorteil dies überhaupt verspricht. Nun, auch das ist relativ intuitiv, bzw. einfach zu verstehen. Wenn man davon ausgeht, dass der Punkt oder der Bereich des Sticking Points jener Teil der Bewegung ist, welcher dem Trainierenden am schwersten fällt, dann ist es sogleich auch der limitierende Bereich, welcher verhindert, dass der Trainierende nicht zum Beispiel mehr Gewicht bei entsprechender Bewegung bewältigen kann. Folglich könnte durch die genaue Identifikation eines Sticking Points dieser womöglich gezielt im Training mit einbezogen werden, geklärt werden, warum genau dieser eben dort auftritt und auf welche Weise er überwunden werden könnte.

Kommen wir also zu einigen postulierten Möglichkeiten, wie man Sticking Point denn nun genauer definieren könnte. Wenn man sich die obige vage Beschreibung von Sticking Points vor Augen führt, dann ist unschwer zu erkennen, dass an mehreren früheren Punkten bereits von ähnlichen Aspekten gesprochen wurde. Und zwar ist dabei die Rede von Kraftkurven. Im Kontext von Kraftkurven und Widerstandsprofilen, geht es mitunter ja auch darum, dass einem Trainierenden im Laufe einer Bewegung unterschiedliche Anforderungen zukommen, sodass der Anstrengungsgrad, der damit einhergeht, über die Bewegung variiert. Dabei wurden bereits die wichtigsten Faktoren aufgegriffen, welche hinter jenen Kraftkurven stecken, seien es Aspekte der Krafterzeugung der Muskeln, muskuläre Hebelarme bis hin zum Widerstandsprofil. Wenn es nun aber um Sticking Points geht, geht es neben all dem speziell um die Frage, wie man bei einer gegebenen Bewegung nun auf einen jeweiligen Sticking Point schließt und ob es sich dabei tatsächlich um eine mehr oder weniger exakte Stelle oder vielmehr um eine breiter gefasste Region handelt. Im Allgemeinen stützen sich viele Versuche, eine genauere Definition des Sticking Points zu formulieren, oftmals auf der Bewegungsgeschwindigkeit, genauer gesagt der Geschwindigkeit mit welcher die jeweilige Last zum Beispiel angehoben wird. Sinkt diese nämlich ab, dann bedeutet dies, dass die vom Trainierenden auf die Last ausgeübte Kraft, welche diese nach oben beschleunigt, geringer ausfällt. Wenn man davon ausgeht, dass solch eine Geschwindigkeitsreduktion zustande kommt, ohne dass der Trainierende bewusst die Geschwindigkeit verlangsamen will, dann deutet dies darauf hin, dass, aus welchem Grund auch immer, weniger Kraft auf die Last ausgeübt wird, sei es, weil sich muskuläre Hebel ändern, die Längenposition oder zum Beispiel auch wegen des Widerstandsprofils. In diesem Sinne wird der Sticking Point oft auch als der Punkt im Bewegungsbereich während einer Übung verstanden, an dem die Aufwärtsgeschwindigkeit der Last abnimmt oder gar zum Stillstand kommt. Doch so intuitiv solch eine Definition auch erscheinen mag, so tun sich bei genauerem Hinsehen einige Ungereimtheiten auf. Vorausgesetzt, dass die Last sich sowohl zu Beginn als auch am Ende einer Bewegung in Ruhe befindet, was bei den meisten Trainingsübungen der Fall ist, dann sind dies beides Punkte, von denen aus die Bewegungsgeschwindigkeit der Last nicht weiter abnehmen kann, bzw. eine sich mit einer Geschwindigkeit >0 bewegende Last hin zu jenen Punkten langsamer werden muss, was aber an sich noch keinen Sticking Point darstellt. Nun könnte man argumentieren, dass besagte Definition den Bewegungsbeginn und das Bewegungsende (bzw. den Umkehrpunkt) außen vor lässt und nur die Bewegung dazwischen umfasst. Aber auch wenn man dies voraussetzt, spezifiziert jene Definition ebenso nicht, ob der Sticking Point nun letztendlich dort liegt, wo die Geschwindigkeit abzunehmen beginnt oder aber wo sie ihr Minimum erreicht, was natürlich einen Unterschied hinsichtlich der Stelle/Region des Sticking Points machen würde. Eine bloße Geschwindigkeitsreduktion scheint zu unpräzise zu sein, so mal in einer realen Situation das Bewegungstempo sowieso kein konstanter Wert ist, sondern immer mehr oder weniger variiert, weil eben sehr viele Variablen mit einspielen. Von einer reinen Reduzierung der Geschwindigkeit gegenüber ihrem Maximum automatisch auf einen Leistungsengpass zu schließen, scheint damit etwas zu weit gegriffen. Der Punkt, an dem die Geschwindigkeit ihr Minimum erreicht, kann hingegen per Definition eigentlich nicht jener Punkt sein, wo es dem Trainierenden am schwersten fällt, die Last zu beschleunigen, weil die Bewegungsgeschwindigkeit vom Punkt der minimalen Geschwindigkeit definitionsgemäß wieder zunimmt, was bedeutet, dass an jenem Punkt ausreichend Kraft auf die Last ausgeübt wird, um diese nach oben zu beschleunigen.

Versuche diese Probleme zu umgehen, umfassen zum Beispiel eine Ausweitung dessen, was man als Sticking Point verstehen sollte, indem dieser eben nicht als bestimmter Punkt, sondern vielmehr als Region angesehen wird. Mit anderen Worten, der Sticking Point könnte somit als Teil des Bewegungsbereichs verstanden werden, welcher sich zwischen dem ersten Höchstwert der Geschwindigkeit, mit der sich die Last bewegt, und ihrem ersten lokalen Minimum danach aufspannt. Aber auch diese Definitionen kommt nicht besonders weit. So sind geschwindigkeitsbasierte Definitionen grundsätzlich nicht wirklich dazu in der Lage, die Möglichkeit von Sticking Points am Ende einer Bewegung zu erklären, weil dann kein lokales Geschwindigkeits-Minimum vorhanden ist. Und auch die Integration des Bewegungsendes als Minimum funktioniert nicht wirklich, eben weil die Bewegung so oder so im Stillstand endet und demnach die Geschwindigkeit hin zu diesem Punkt auch früher oder später abnehmen muss, auch wenn dieser Teil der Bewegung nicht besonders anspruchsvoll ist. Trotzdem kommt es in vielen Situationen durchaus vor, dass die Bewegung zunehmend schwerer wird.

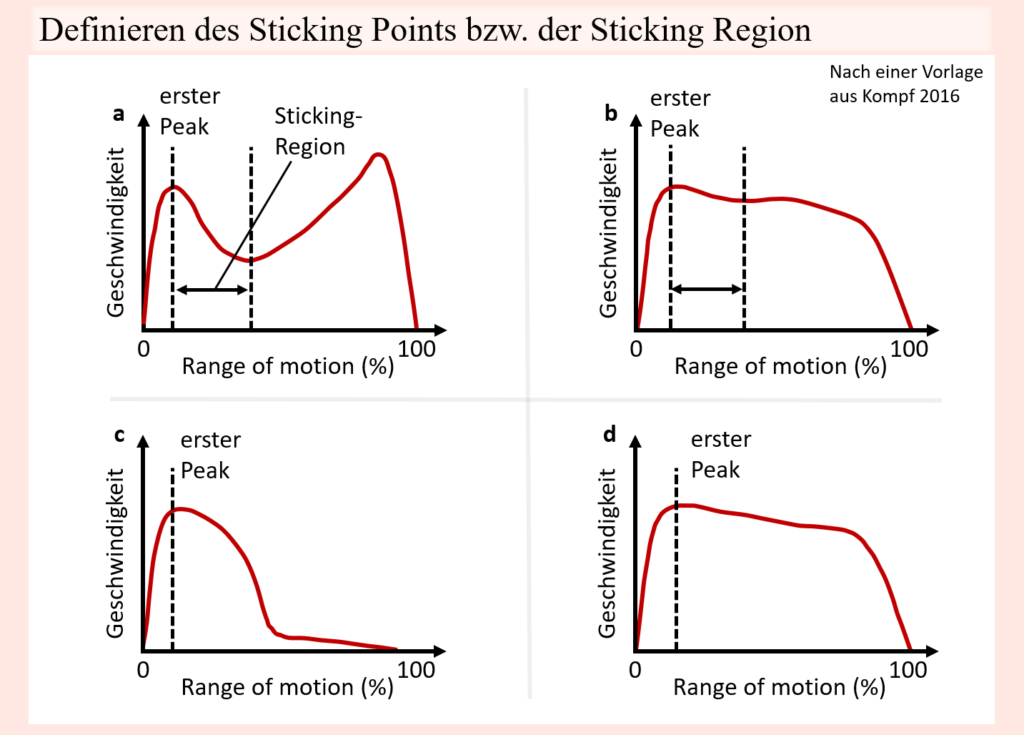
Anstelle der Geschwindigkeit der Last konzentrieren sich andere Definitionen auf die Kraft, welche der Trainierende auf die Last ausübt, und der Kraft, die der Bewegung Widerstand leistet (meistens das Gewicht der Last), wobei dies natürlich mit der Geschwindigkeitsänderungsrate in Verbindung steht. In diesem Kontext könnten Sticking Points- oder Regionen Abschnitte von Bewegungen sein, wo der Trainierende Schwierigkeiten hat Kraft gegen die Last auszuüben. Auch das ist aber nicht ganz kohärent, wenn man zum Beispiel bedenkt, dass die erzeugten Muskelkräfte bei höherer Geschwindigkeit abnehmen. So könnte die auf die Last ausgeübte Kraft bei einer hohen Bewegungsgeschwindigkeit geringer ausfallen als bei geringerer Geschwindigkeit, wobei es aber absurd ist, deswegen gleich auch davon auszugehen, dass sich der Sticking Point im Bereich der größten Bewegungsgeschwindigkeit befindet.

Bei einer anderen Definition wird der Sticking Point als der schwächste Punkt im Bewegungsbereich einer Übung definiert, welcher dort auftritt, wo der äußere Widerstand den größten mechanischen Vorteil hat. Dies bezieht sich im Wesentlichen auf die Kraftkurve, welche, wie an einem vorherigen Punkt bereits geschildert, vor allem vom Widerstandsprofil (Betrag einwirkender Kräfte + Hebelarme auf Gelenke) bestimmt wird. Dennoch ist das Widerstandsprofil nicht der einzige Faktor, welcher in die Kraftkurve miteinfließt, was sich auch wieder darin zeigt, dass die anspruchsvollste Stelle bei bestimmten Bewegungen durchaus dort auftreten kann, wo der äußere Widerstand einen vergleichsweise geringen mechanischen Vorteil hat. So wird der Sticking Point zum Beispiel beim Bankdrücken als auch beim Kreuzheben oftmals auch am Ende des Bewegungsbereichs (Ende der Konzentrik) beobachtet, obwohl in beiden Fällen diese Positionen für den Trainierenden biomechanisch vorteilhafter sind als andere Positionen, wenn lediglich das Widerstandsprofil betrachtet wird. Das zeigt natürlich auf, dass auch diese Definition etwas zu kurz kommt.

All diese verschiedenen Definitionen und die Schwierigkeiten, welche bei allen zum Vorschein kommen, weisen darauf hin, dass diese zwar in die richtige Richtung gehen, sie aber alle daran scheitern, die tatsächliche Komplexität des Ganzen zu erfassen. Mitunter geht dies wahrscheinlich auch auf die Missverständnisse und unbegründete Simplifizierung rund um das Prinzip der Kraftkurven zurück, worauf an anderen Stellen bereits mehrmals eingegangen wurde. So ist es zwar tatsächlich so, dass das Widerstandsprofil wohl der größte Faktor für jeweilige Kraftkurven ist, jedoch spielen auch andere Faktoren mit ein, deren jeweilige Relevanz auch variieren kann. So wird der Sticking Point zum Beispiel bei einer Kniebeuge auch grob mit den (bio)mechanischen Begebenheiten zusammenpassen, sodass dieser meistens in der unteren Hälfte der Bewegung eintritt. Dennoch gibt es auch hier zum einen Ausnahmen und zum anderen deckt sich der Sticking Point in der Regel sogar nicht genau mit dem Widerstandsprofiel. Dies sollte im weiter unten angeführten Textabschnitt, zu den Möglichkeiten, wie Sticking Points überwunden bzw. beeinflusst werden können, deutlicher werden. Abseits des alleinigen Widerstandsprofils gilt es so zum Beispiel auch zu beachten, dass z.B. die passiven Kräfte am Beispiel einer Kniebeuge im Laufe der Konzentrik abnehmen, was den Sticking Point durchaus in eine höhere Position verschieben kann, vor allem wenn beispielsweise die aktiv erzeugten Muskelkräfte aufgrund muskulärer Ermüdung abfallen.

Gerade wenn es um Bewegungen geht, welche mehrere Gelenke umfassen, sind die effektiven Kraftkurven komplex und beinhaltet eine nicht lineare Kombination von Kraftkurven einzelner Gelenke und Muskeln. Selbst im einfachsten Fall, also einer eingelenkigen Bewegung, ist die resultierende Kraftkurve aufgrund des Zusammenspiels von Kraft-Längen- und Kraft-Geschwindigkeits-Eigenschaften sowie der wechselnden Hebel seitens des Muskels als auch der Last, sowie eventuell vorhandener Ermüdung nicht einfach vorherzusagen. Das wiederum überträgt sich natürlich auch auf das Entstehen und die Lokalisation von Sticking Points. Um Sticking Points also vollständig zu verstehen, müssen daher alle diese Faktoren berücksichtigt werden, wodurch die Erklärung eines bestimmten Sticking Points auch eine gründliche Analyse des jeweiligen Trainierenden im Kontext, in dem der Sticking Point beobachtet wird, erfordert.

Sticking Points akut beeinflussen und überwinden

Wenn man isokinetische Trainingsmaschinen mal außen vor lässt, dann weisen im Grunde alle Trainingsbewegungen mehr oder weniger ausgeprägte Sticking Points, also Bewegungsbereiche, welche anspruchsvoller sind, auf. Die meisten Faktoren, welche diese bestimmen, können vom Trainierenden nicht wirklich beeinflusst werden, schließlich geht es dabei schlichtweg um (bio)mechanische Gegebenheiten, wie groß muskuläre Hebelarme sind, wie groß der Betrag der extern einwirkenden Kräfte ist, wie groß deren Hebelarme auf Gelenke ausfallen, in welcher Längenposition sich die Muskulatur befindet usw. All diese Dinge sind Gegebenheiten, die zwar dafür sorgen, dass es zum Beispiel schwierig wird Sticking Points in einer bestimmten Bewegung zu verallgemeinern, aber ebenso sind es Faktoren, welche vom Trainierenden zumindest zum Teil gewissermaßen so hingenommen werden müssen, also nicht akut beeinflusst werden können. So aber nicht bei einigen anderen Faktoren, welche vielmehr ganz gezielt, also bewusst oder auch unbewusst eingesetzt werden, um zum Beispiel Sticking Points zu überwinden. Die Rede ist hier vor allem von zwei Variablen, nämlich einer schlichten Bewegungsänderung und dem Impuls.

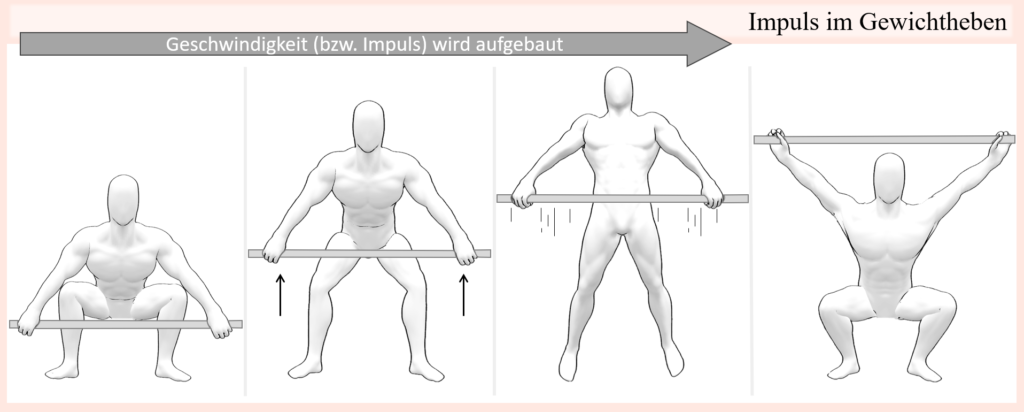
Die Rolle der Bewegungsgeschwindigkeit wurde schon mehrmals in diesem Kontext angesprochen. Nur weil zum Beispiel eine Hantelstange 100 kg wiegt, heißt das nicht, dass der Widerstand auf den Trainierenden, welcher sich entgegen dieser Gewichtskraft bewegt, auch immer konstant ausfällt. In Newtons Trägheitsgesetz, welches mitunter besagt, dass ein sich bewegender Körper auch in Bewegung bleibt, wird das natürlich auch aufgegriffen. Wird die Hantelstange durch ausreichend Kraft nach oben beschleunigt, dann ist im darauffolgenden Bewegungsabschnitt nicht mehr so viel Kraft nötig, um diese Aufwärtsbewegung zu leiten. Genau dies machen sich zum Beispiel olympische Gewichtheber zunutze, indem sie die am Boden liegende Hantelstange maximal nach oben beschleunigen, daraufhin die kurze Zeitspanne, in welcher sich die Hantel durch diesen „Schwung“ auch ohne, dass sie weiterhin übermäßig Kraft auf sie ausüben müssen, nutzen, um ihren Körper unter die Stange zu bringen. Der „Schwung“, von dem hierbei die Rede ist, wird in der Physik als Impuls bezeichnet. Dieser Impuls ist gleich das Resultat aus der Masse des Körpers × seiner Geschwindigkeit. Damit ist der Impuls („Schwung“) also größer, je größer die Masse des Körpers und je schneller er sich bewegt. Kennengelernt haben wir dies unter Verwendung des Begriffes Trägheit bereits bei dem Vergleich von Fahrzeugen mit unterschiedlicher Masse. So erfordert es zwar mehr Kraft ein schweres Fahrzeug wie einen LKW aus der Ruhe auf eine bestimmte Geschwindigkeit zu beschleunigen als vergleichsweise ein Fahrrad, jedoch ist es andererseits dann umso schwerer den sich bewegenden LKW zu stoppen. Der Grund dafür ist seine vergleichsweise große Masse, woraus sich bei gegebener Geschwindigkeit ein entsprechend größerer Impuls ergibt. Innerhalb eines Vakuums würde der Impuls eines kräftefreien Körpers immer konstant bleiben (was so viel bedeutet, dass er seinen Bewegungszustand beibehält). In realen Situationen bewirken aber andere Kräfte, wie Reibungskräfte, dass dieser Impuls im Laufe der Zeit abnimmt, sodass der LKW irgendwann stehen bleibt, wenn der Fahrer das Gaspedal loslässt. Übertragen auf eine sich bewegende Hantel im Training, kann dies natürlich auch sehr schön aufgezeigt werden. Wird die Hantel in der exzentrischen Bewegungsphase besonders schnell abgelassen, dann gewinnt diese durch die höhere Geschwindigkeit einen entsprechend größeren Impuls, sodass am Umkehrpunkt, also dort wo die Hantel dann doch abgebremst werden muss, um folglich die konzentrische Bewegungsphase zu starten, durch den mitgebrachten „Schwung“ der Hantel eine größere Belastung auf den Bewegungsapparat entsteht, sodass die aufzubringende Kraft, um die Hantel abzubremsen, umso größer ausfallen muss. Aber das ist nicht alles, denn auf der anderen Seite kann der Impuls auch genutzt werden, um bestimmte Bewegungsphasen zu vereinfachen. Im Falle des Widerstandstrainings, wo die Bewegungsrichtung entgegen einem Widerstand erfolgt, übt also der Trainierende zum Beispiel auf eine Hantel eine Kraft aus, beschleunigt sie dadurch nach oben und gibt ihr einen Impuls mit. Die entgegengesetzte Gewichtskraft der Hantel wiederum zieht sie aber in entgegengesetzte Richtung zum Boden hin und sorgt damit dafür, dass der vom Trainierende mitgegebene Impuls wieder abnimmt. Das ist neben dem Luftwiderstand der Grund, weshalb ein einmaliger Kraftstoß nicht ausreicht, um die Hantel in eine gleichförmige Aufwärtsbewegung zu versetzen. Ist nun aber die ausgeübte Kraft groß genug, und überwiegt die Schwerkraft, dann besteht ein kurzer Zeitraum, indem sich die Hantel durch den mitgegebenen Impuls („Schwung“) nach oben, entgegen der Schwerkraft bewegt, bis die Schwerkraft diesen Impuls wieder auf null bringt. Einfacher ausgedrückt wird die Hantelstange quasi in die Luft geworfen, so wie man auch zum Beispiel einen Fußball in die Luft werfen kann, indem man einen Kraftstoß auf ihn ausübt und ihm somit einen Impuls mitgibt. Der Ball wird sich folglich nach oben bewegen, wobei die auf ihn einwirkende Schwerkraft ihn kontinuierlich abbremst und ihn schließlich wieder in Richtung Erdmittelpunkt hin beschleunigt. Im Falle der Hantel bleibt das Prinzip genau gleich, nur dass natürlich die notwendige Kraft, um diese auf eine bestimmte Geschwindigkeit zu beschleunigen, höher ausfällt, wodurch ein Mensch nicht in der Lage ist, eine schwere Hantel weit in die Luft zu werfen. Der kurze Zeitrahmen aber, wo der Schwung der Hantel noch der Schwerkraft widersteht, wird zum Beispiel im Gewichtheben genutzt, um den Körper unter die Stange zu bringen. Aber auch anderweitig wird dies, bewusst oder auch unbewusst eingesetzt, um Sticking Points zu überwinden. Denn indem in „leichteren“ Bereichen der Bewegung, dort wo dies noch möglich ist, eine möglichst hohe Geschwindigkeit erreicht wird, können darauffolgende „schwerere“ Bereiche, worunter natürlich auch Sticking Points fallen, besser überbrückt werden. Im Grunde schafft man dadurch gewissermaßen einen variablen Widerstand, der besser auf die jeweilige Kraftkurve angepasst ist, auch wenn die Last an sich konstant bleibt. Dies kennt man aus der Trainingspraxis nur zu gut, wenn zum Beispiel bei Klimmzügen im unteren Bereich eine höhere Bewegungsgeschwindigkeit erreicht wird, sodass der „Schwung“ folglich genutzt werden kann, um den kompletten konzentrischen Bewegungsabschnitt zu durchlaufen, wohingegen dies bei einer durchweg langsamen Bewegungsgeschwindigkeit vielleicht nicht mehr möglich gewesen wäre. Im Kontext zahlreicher Bewegungen und Sportarten wird die Bewegungsgeschwindigkeit gezielt von Sportlern eingesetzt, aber auch unterbewusst tendiert man dazu, sich dies zunutze zu machen, wenn eine Bewegung ansonsten nicht, oder nur besonders schwer, ausgeführt werden könnte. Tatsächlich spricht man hierbei umgangssprachlich im Trainingskontext sogar von „Schwung“, wobei dies oftmals eher mit negativen Aspekten wie einer „unsauberen“ Bewegungsausführung assoziiert wird. Jetzt wissen wir, dass mit „Schwung“ konkreter ausgedrückt der Impuls gemeint ist und dass dieser keineswegs intrinsisch „schlecht“ ist. Wenn man davon ausgeht, dass es förderlich sein kann, Kraftkurven und Widerstandsprofile abzugleichen, kann die Bewegungsgeschwindigkeit vielmehr ein sehr hilfreiches Werkzeug sein, um genau dies, ohne einen tatsächlich variierenden Widerstand, wie dies herkömmlicherweise bei vielen Trainingsmaschinen der Fall ist, zu erreichen. Ebenso ist es ein fundamentaler Bestandteil zahlreicher Sportarten, wie das olympische Gewichtheben natürlich bestens aufzeigt.

Die mechanische Beschreibung von Gewichtskräften als Bewegungswiderstand erweist sich wie gesagt im Vergleich oft relativ einfach, weil z.B. gerade im Falle von Trainingshanteln die Masse (bzw. das „Gewicht“) bereits auf den Hanteln bzw. Gewichtsscheiben angegeben ist und die Kraftrichtung immer zum Erdmittelpunkt hin verläuft. Damit hat man nämlich einen Betrag als auch eine Richtung, wodurch man gleichwohl im Kontext eines Kraftangriffspunktes, also dem Punkt, wo eine solche Kraft auf den Körper einwirkt, sogleich auch Kräfte und Hebelarme auf Gelenke folgern kann. Genau das wurde an vorherigen Punkten ja bereits mehrmals aufgezeigt.

Neben der Bewegungsgeschwindigkeit bieten auch schlichtweg Bewegungs- bzw. Positionsveränderung im Laufe bestimmter Bewegungen die Möglichkeit, die gegenwärtigen biomechanischen Bedingungen zu beeinflussen und zum Beispiel Sticking Points zu überwinden. Zumindest wenn es um Bewegungen geht, welche offenen kinematische Ketten entsprechen, lassen sich die von einer Last erzeugten Gelenk-Drehmomente und folglich die jeweiligen Anforderungen entsprechender Muskeln, um jener Last entgegenzutreten, anhand von Hebelarmen ausgehend von der Wirkungskraftlinie erkennen. Ob es sich nun um eine Bewegung handelt, welche nur ein Gelenk betrifft, oder aber um eine mehrgelenkige Bewegung, oftmals besteht die Möglichkeit durch Änderungen der Körperposition auch die gegenwärtigen biomechanischen Begebenheiten zu verändern. Sind solche Positionsänderungen möglich, dann kann zum Beispiel die Lage jeweiliger Gelenke im Verhältnis zur Wirkungskraftlinie verschoben oder auch die Längenpositionen bestimmter Muskeln verändert werden. In weiter unten folgenden Textabschnitten werden wir genau dies in Form sogenannter Kompensationsbewegungen noch genauer kennenlernen. Hierbei kommt es gerade in grenznahen Situationen, sprich, wenn einer bestimmten Bewegung ein Widerstand gegenübersteht, welcher nur sehr schwer bewältigt werden kann, durch solche Positionsveränderungen zu unwillkürlichen Lastverschiebungen, welche den Zweck haben, den Bewegungsapparat in stärkere Positionen zu bringen, um so den Widerstand zu überwinden. Ein einfaches Beispiel, wo etwas in die Richtung passiert, kann man sich bei ganz normalen Bizeps curls aber bereits vor Augen führen. Wird jene Bewegung mit einer freien Hantel ausgeführt, dann verläuft die Widerstandskurve in etwa glockenförmig, sprich in der Startposition bei ausgestreckten Armen verläuft die Wirkungskraftlinie durch den Ellbogen, mit zunehmender Beugung entfernt sich diese aber vom Rotationszentrum und erreicht das Maximum, sobald der Unterarm horizontal zum Boden steht. Wird dieser Punkt überschritten, dann nähert sich die Wirkungskraftlinie wieder dem Drehpunkt an. Daraus folgt, dass der anspruchsvollste Abschnitt der Bewegung, also der Sticking Point bzw. die Sticking Region sich in diesem mittleren Bereich befindet, eben weil die Last dort einen so großen mechanischen Vorteil aufweist. Aus dem obigen Teil zur Geschwindigkeit wird bereits ersichtlich, dass jene Sticking Region nun leichter überwunden werden kann, wenn im vorangehenden Teil der Bewegung eine hohe Geschwindigkeit erreicht wird, umgangssprachlich, indem man Schwung aufbaut.

Aber das ist nicht alles, vor allem wenn die zu bewegende Last sehr schwer ist, dann kann bewusst oder auch unbewusst auch eine Positionsveränderung zusätzlich Abhilfe bieten, indem die Ellbogen weiter an die Wirkungskraftlinie bzw. in eine senkrechtere Position gebracht werden. Hierdurch verringert sich natürlich der Hebelarm der Last und damit sogleich auch der Widerstand für die Muskeln. Klassischerweise wird dies mit dem im unteren Bereich aufgebauten Impuls kombiniert, sodass der Schwung genutzt wird, um die Ellbogen unter die Stange zu bringen.

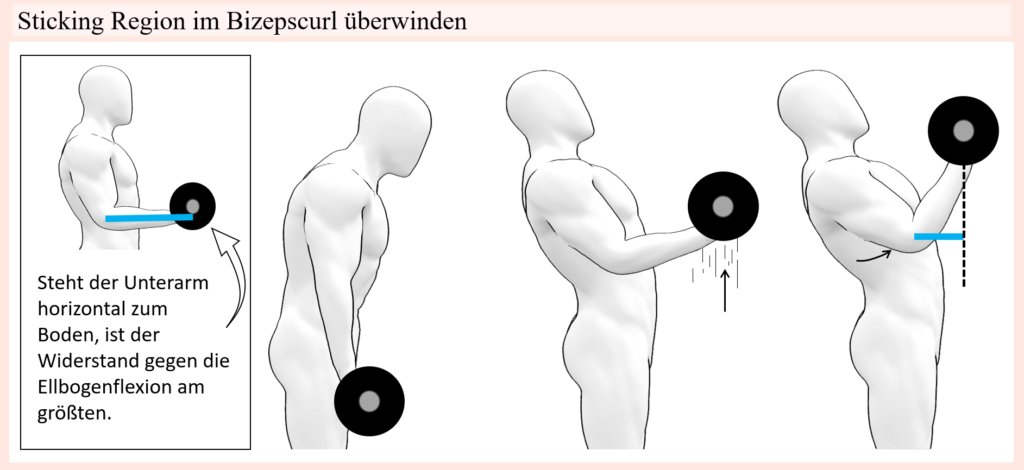
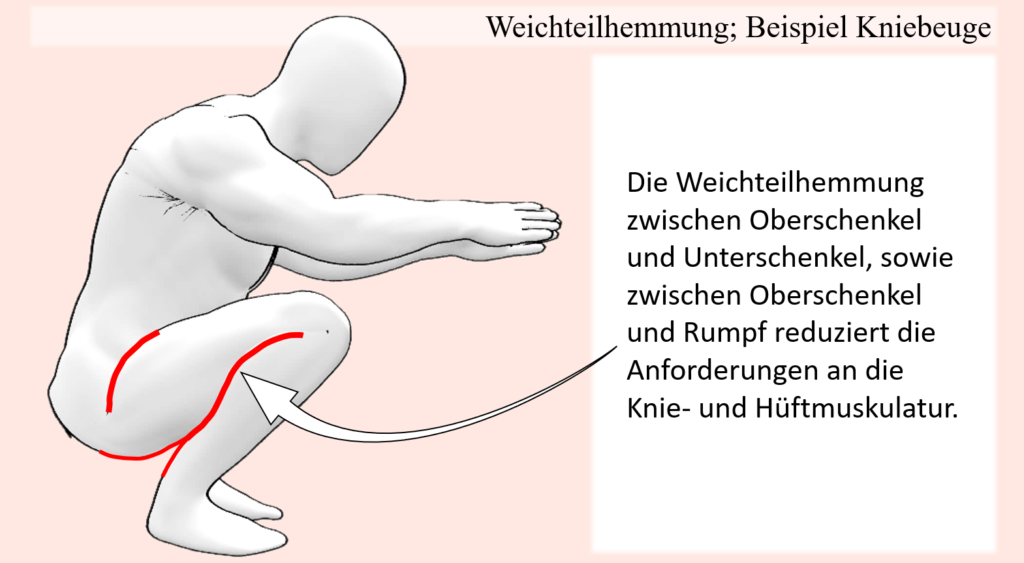
Neben veränderten Hebelverhältnissen und damit einhergehenden Widerstandsprofilen, kann andererseits aber auch die Kraft seitens des Trainierenden beeinflusst werden. Wird ein Muskel zum Beispiel in eine längere Position gebracht, dann befindet er sich in einer stärkeren Position, weil im Vergleich zu einer stark kontrahierten Position unter Umständen mehr Querbrücken ablaufen können und vor allem die passiven Kräfte mit zunehmender Länge ansteigen. Ebenso können bei schneller Dehnung durch einen verstärkten Dehnungs-Verkürzungs-Zyklus unter Umständen weitere passive Kräfte zugutekommen. Wenn an vorherigen Punkten die Rede von passiven Kräften war, dann ging es vor allem um passive, Bindegewebe-Strukturen wie Sehnen oder auch den Titin-Kräften im Inneren der Muskelfasern. Dabei sei aber gesagt, dass dies nicht alles ist, denn im Grunde gelten jegliche anderen Strukturen, welche dem Widerstand Gegenhalt bieten als passive Kräfte. Neben passiven Dehn-Kräften der Muskel-Sehnen-Einheiten selbst ist hier vor allem die Weichteilhemmung interessant. Bei der anatomischen Betrachtung des Bewegungsapparates im Kontext des Bewegungsspielraumes eines Gelenkes wurde bereits angesprochen, dass dieser durch das Gelenk umliegendes weiches Gewebe limitiert sein kann. Berühren sich bei einer Gelenkbewegung zwei Körperteile, die mit weichem Gewebe (vor allem Muskeln und Körperfett) umgeben sind, dann werden diese gegeneinandergedrückt. Dies limitiert unter Umständen nicht nur den Bewegungsradius des Gelenkes, sondern steht einem weiteren Zusammendrücken auch als Widerstand entgegen. Wenn nun also eine Last Gelenkbewegungen bewirkt, wo es zu solch einer Weichteilhemmung kommt, dann sorgt ein gewisser Anteil jener Kraft für eben jenes Zusammendrücken der Weichteile, was sogleich bedeutet, dass dieser Anteil, der sozusagen von der Weichteilhemmung übernommen wird, nicht den Muskeln als Widerstand gegenübersteht.

Kompensationsbewegungen

Nun kommen wir zum eigentlichen Haupt-Thema des vorliegenden Abschnittes, den Kompensationsbewegungen. Was Kompensationsbewegungen im Allgemeinen sind, wurde etwas weiter oben ja bereits erwähnt. Demnach sind es gewissermaßen Ausweichbewegungen, welche vor allem bei grenznaher Belastung vom Körper ergriffen werden, um die zu geringe Kraft in der eigentlichen Bewegung zu kompensieren. Damit wird auch klar, warum hier vor allem die Rede von grenznahen Situationen ist, was im Falle des Widerstandstrainings bedeuten kann, dass eine bestimmte Bewegung mit einer sehr hohen oder gar maximalen Last als Widerstand, oder auch eine Bewegung andauernd, bis hin zur Erschöpfung ausgeführt wird. In Situationen, welche nicht besonders anspruchsvoll sind, müssen nicht zwingend Ausweichbewegungen zum Vorschein kommen, weil die Anforderungen entsprechender Muskeln nicht ausgereizt werden. Wenn der Bewegungsapparat aber an seine Grenzen kommt, muss er den Weg maximaler Kraft bzw. minimalen Widerstandes wählen, um die Bewegung überhaupt ausführen zu können. Wie solche Kompensationsbewegungen dabei aussehen, kommt dann natürlich auf die jeweilige Bewegung an. Grundlegend kann man aber zwischen zwei Möglichkeiten unterscheiden.

So werden bei jeder Bewegung bestimmte Muskeln bzw. Muskelgruppen belastet. In einigen Fällen handelt es sich dabei vielleicht nur um eine bestimmte Muskelgruppe, wohingegen bei anderen Bewegungen eine ganze Reihe von Gelenken und Muskelgruppen beteiligt sind. Vor allem, wenn letzteres der Fall ist, dann kann die genaue Lastverteilung auf besagte Gelenke bzw. Muskelgruppen durch kleinere Bewegungsänderungen oftmals variieren. Und genau hier liegt der Quell besagter Ausweich- bzw. Kompensationsbewegungen. Was nämlich passiert, wenn eine der beteiligten Muskelgruppen den ihr entgegenstehenden Widerstand nicht standhalten bzw. überwinden kann, dann muss dieser Widerstand für jene Muskulatur möglichst verringert werden. Dies passiert, indem der Hebelarm der Last auf besagtes Gelenk verringert wird. Das entspricht aber wohlgemerkt keinem Kraftersparnis, sondern die zu bewegende Last bleibt natürlich dieselbe, nur die Lastverteilung auf besagte Gelenke wird verändert. Mit anderen Worten, das schwächste Glied der Kette muss kompensiert werden, indem die Last vermehrt auf andere Gelenke und Muskeln verschoben wird. Nun weiß man von außen betrachtet wohlgemerkt nicht genau, wie diese Lastverteilung aussieht und wie viel Kraft jeweilige Muskeln im Laufe der Bewegung erzeugen. Genau hier kommt uns aber die bereits zu Beginn angesprochene Verbindung von Kraft und Bewegung zugute, weil man ausgehend der Bewegung nun folgern kann, welche Strukturen bzw. Muskeln stärker belastet werden und welche vielmehr entlastet werden. Wie sich einzelne Gelenke bewegen, ist schließlich das Resultat der dort wirkenden Kräfte bzw. Drehmomente, woraus folgt, dass die Bewegung als Ganzes vor allem von den extern wirkenden Kräften und der Krafterzeugung jeweiliger Muskeln abhängt. Damit hat eine Lastverteilung und damit einhergehende Kraftproduktion der jeweils zuständigen Muskeln besagte Bewegungsänderungen zur Folge. Auch wenn man die genaue Aktivität der Muskeln also nicht kennt, kann ausgehend von der beobachteten Bewegung darauf geschlossen werden. Bei hoher Last oder auch Erschöpfung kommt es dabei ganz automatisch zu Kompensationsbewegungen, weil der Körper wie gesagt in solchen Situationen den Weg maximaler Kraft gehen muss, was so viel bedeutet, als dass zu schwache Muskeln, welche die Bewegung nicht tragen können, mindestens so weit entlastet werden, als dass sie den ihnen auferlegten Widerstand bewältigen können. Dadurch, dass eine Bewegung in der Regel aber nicht durchweg gleich anspruchsvoll erscheint, sprich, das Widerstandsprofil und damit auch die Anforderungen an die jeweiligen Muskeln über die Bewegung hinweg meistens variieren, ist eine Bewegung meist nicht durchweg grenznah. Das heißt, wenn man davon ausgeht, dass es um eine dynamische Bewegung (also Konzentrik und Exzentrik) geht, als auch wegen des Widerstandsprofils bestimmte Bereiche anspruchsvoller als andere sind, dann kann man zunächst eingrenzen, dass das „grenznahe“ sich auf die konzentrische Bewegungsphase beschränkt. Der Grund hierfür ist ganz einfach. In der exzentrischen Bewegungsphase geht es nicht um ein Überwinden eines Widerstandes, sondern um ein Abbremsen, was an sich schon mal einen geringeren Kraftaufwand seitens der Muskulatur erfordert. Ebenso kommen der Exzentrik zusätzlich vermehrt passive Kräfte zugute, sodass dadurch die aktiv erzeugten Muskelkräfte unter Umständen noch geringer ausfallen können. Handelt es sich also beispielsweise um eine dynamische Bewegung, welche mit einer maximalen Last ausgeführt wird, dann heißt dies so viel, dass in der konzentrischen Bewegungsphase keine höhere Last überwunden werden könnte. Für die Exzentrik alleine würde dieses Maximum hingegen höher ausfallen, was bedeutet, dass Muskeln, die in der Konzentrik womöglich an ihre Grenzen stoßen, in der Exzentrik die auf ihnen liegende Last wahrscheinlich ohne größere Probleme handhaben können. Das wiederum bedeutet auch, dass eventuelle Kompensationsbewegungen in diesem konzentrischen Bewegungsbereich zum Vorschein kommen und sich als Abweichung zum Bewegungspfad der vorangehenden Exzentrik sichtbar machen. Nun variieren aber auch innerhalb dieser konzentrischen Bewegungsphase die Anforderungen an entsprechende Muskeln, sodass bestimmte Punkte bzw. Regionen als Sticking Points beschrieben werden können. Auch hier gilt also, wenn eine dynamische Bewegung mit maximaler Last bewältigt wird, dass gerade in den anspruchsvollsten Bereichen, also der Sticking Region der Bewegung, keine höhere Last überwunden werden könnte. In anderen Bewegungsabschnitten, in denen die mechanischen Begebenheiten vielleicht günstiger sind, könnte hingegen noch eine höhere Last überwunden werden. Für die Kompensationsbewegungen bedeutet dies, dass jene Ausweichbewegungen, welche daraus resultieren, dass gewisse Muskeln der Last nicht standhalten, vor allem in eben jenen Regionen auftreten. Auch wenn wir bislang keine einheitliche Definition für Sticking Points bzw. Sticking Regionen haben, zeigen sich diese in einer Bewegung, welche zum Beispiel mit einer supramaximalen Last ausgeführt wird als jene Region, wo es dem Trainierenden nicht mehr möglich ist, die Last weiter, entgegen der Schwerkraft zu beschleunigen, wobei demnach eine Geschwindigkeitsreduktion einhergeht. Unabhängig davon, welchen genauen Punkt oder welchen genauen Bereich man hierbei nun als Sticking Region definiert, folgt daraus ein relativ simples Prozedere, durch welches Schwachstellen einer Bewegung identifiziert werden können, indem man anhand einer jeweiligen grenznahen Bewegung eine Handvoll Fragen stellt:

An welchen Punkt der Bewegung begann die Geschwindigkeitsabnahme?
Was waren in jener Position die Anforderungen an jeweilige Muskeln?
Was waren in jener Position die internen biomechanischen Begebenheiten?
Wie hat der Körper dies kompensiert?
Welche Muskelgruppe wurden demnach entlastet?

Wenn man nun also weiß, welche Gelenke und Muskeln in grenznahen Situationen entlastet werden, dann deutet dies darauf hin, dass jene Muskeln also im Verhältnis zu den anderen, welche hierfür kompensieren müssen, als muskuläre Schwächen anzusehen sind. Und wie man so schön sagt, ist eine Kette nur so belastbar, wie ihr schwächstes Glied. Dies gilt gewissermaßen natürlich auch für den Bewegungsapparat, denn würden jeweilige Schwachpunkte die ihnen zukommenden Anforderungen bewältigen können, sodass keine Ausweichbewegung nötig wäre, dann müssten andere Muskelgruppen auch nicht für sie kompensieren und im Umkehrschluss könnte somit einer höheren Last widerstanden werden. Wohlgemerkt, bei geschlossenen kinematischen Ketten kann eine Lastverschiebung sogar bei einer äußerlich gleichbleibenden Bewegung stattfinden, weswegen Analysen bezogen auf die beobachtbare Bewegung auch weniger zuverlässig als im Falle offener kinematischer Ketten sind.

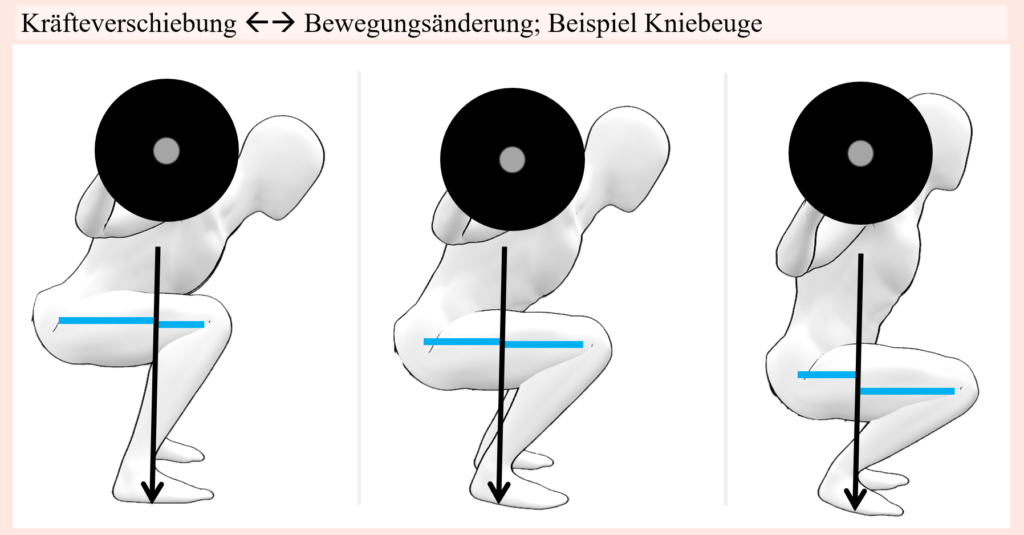
Bei anderen Bewegungen wiederum kann es nun aber auch der Fall sein, dass die Last überhaupt erst gar nicht zwischen verschiedenen Muskelgruppen verschoben werden kann. Denn wenn es sich um eine offene kinematische Bewegungskette handelt, wobei die involvierten Gelenke unabhängig voneinander bewegt werden müssen, und die Zielbewegung nun mal eine bestimmte Bewegung eines bestimmten Gelenkes mit einschließt, dann ist natürlich anatomisch determiniert, welche Muskeln denn hierfür zuständig sind. In solch einem Falle kann die Last also nicht verschoben und jene Muskulatur auch nicht entlastet werden, es sei denn, die extern einwirkenden Hebelarme seitens der Last können verringert werden. Falls letzteres aber nicht, oder nicht signifikant möglich ist, dann können Bewegungen in grenznahen Situationen als Kompensationsbewegung zum Vorschein kommen, welche besagten Muskel- bzw. Muskelgruppe in eine stärkere Position bringen, sei es eine längere Position, oder gar eine Position mit einem größeren muskulären Hebelarm, sodass dem Widerstand dadurch etwas besser Paroli geboten werden kann.

Kommen wir nun also zu einer etwas konkreteren Betrachtung von Kompensationsbewegungen anhand von Beispielen. Dabei sehen wir uns zunächst einige einfachere Bewegungen an, oder besser gesagt Bewegungen, in denen keine oder kaum eine Lastverschiebung stattfinden kann. Daran anknüpfend wiederum werden anhand drei der gängigsten frei ausgeführten Mehrgelenksbewegungen, nämlich der Kniebeuge, dem Kreuzheben und dem Bankdrücken, eben solche Lastverschiebungen und verschiedene Kompensationsbewegungen betrachtet. Dabei folgen wir einem recht simplen Schema, in welchem es zunächst darum geht, belastete Gelenke, extern wirkende Kräfte und zuständige Muskeln zu identifizieren. Darauffolgend können wir dann im Sinne der Kompensationsbewegungen darauf eingehen, inwiefern bestimmte Muskeln entlastet werden können, oder aber wie belastete Muskeln in mechanisch günstigere Positionen gebracht werden können.

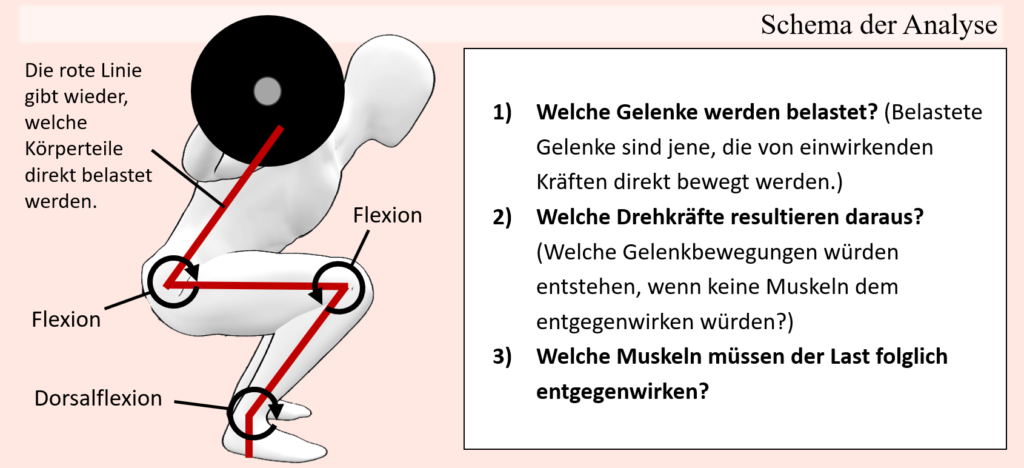
Zunächst geht es also darum, die Bewegung etwas genauer zu definieren, sprich, welche Gelenke sich bewegen und in welche Richtung sie es tun. Das verrät nicht nur über welche Raumebenen sich die Bewegung erstreckt und über welche Betrachtungsebenen es Sinn macht, die Bewegung zu betrachten, sondern auch welche Muskeln beteiligt sein könnten, schließlich sind anatomisch gesehen bestimmte Muskeln für bestimmte Gelenkbewegungen zuständig. Im nächsten Schritt geht es nun darum, die wirkenden Kräfte zu identifizieren, sodass man weiß, in welche Richtung das Gelenk durch eine von außen einwirkende Kraft rotiert wird und in welche Richtung die Muskulatur ziehen muss, um die jeweilige Bewegung zu ermöglichen. Nur die Inbezugnahme extern wirkender Kräfte vermag es, die für ein Gelenk zuständigen Muskeln weiter auf die für die jeweilige Bewegung zuständigen Muskeln zu filtert. Denn würde man rein kinematisch eine wiederholte Ellbogenrotation betrachten (Ellbogenbeugung- und Streckung), dann könnte man zwar darauf schließen, dass Ellbogen-beugende als auch Ellbogen-streckende Muskeln für dieses Gelenk zuständig sind, jedoch gibt dies allein noch keine Auskunft darüber, ob nun zum Beispiel eine Hantel den Ellbogen zur Streckung oder ein Seil eines Kabelturmes ihn zur Beugung verleitet, wobei im ersteren Falle die Ellbogenbeuger der Last entgegenwirken müssen und im letzteren die Ellbogenstrecker. Durch Inbezugnahme der wirkenden Kräfte kann also darauf geschlossen werden, um welche Muskeln es letztendlich geht. Daran anknüpfend können dann die Kräftebedingungen im Verlauf der Bewegung festgemacht werden, sprich welche Muskeln welchen Teil der Bewegung ermöglichen bzw. wie stark verschiedene Muskeln in unterschiedlichen Bewegungsabschnitten belastet werden, was natürlich Kompensationsbewegungen mit einschließt. Vorweg sei hierbei noch zu erwähnen, dass die Bewegungsgeschwindigkeit nicht in jedem dieser Beispiele erneut aufgegriffen wird, denn ein stärkerer „Schwung“ kann dabei im Grunde generell als Bewegungsstrategie für die Vollendung einer Bewegung dienen.

Beginnen wir also mit einem einfachen Beispiel. Im Grunde wurde dieses bereits weiter oben beschrieben, weshalb es an diesem Punkt wohl reichen würde, darauf zu verweisen. Die Rede ist vom klassischen Bizepscurl mit einer freien Hantel. Dies ist natürlich eine sehr simple Bewegung, in der hauptsächlich der Ellbogen als bewegliches Gelenk beteiligt ist. Die Widerstandsquelle dieser Bewegung ist die Gewichtskraft des Unterarmes samt der Hand plus natürlich der Hantel, wobei diese der Schwerkraft wegen immer in Richtung Erdmittelpunkt gerichtet sind. Wird die Bewegung also im aufrechten Stand ausgeführt, dann erzeugt die Last dementsprechend ein „Extensions-Drehmoment“ im Ellbogen. Daraus folgt, dass die ellenbogenbeugende Muskulatur dem entgegenwirken muss, wenn der Ellbogen gebeugt werden soll. Wenn man sich nun die Frage stellen sollte, ob die zu überwindende Last in diesem Falle nun auch verschoben werden könnte, dann wird man schnell zum Schluss kommen, dass dies hier nicht möglich ist. Soll der Ellbogen gebeugt werden, müssen dies die ellenbogenbeugenden Muskeln erledigen, womit die Last zwangsweise auf jenen Muskeln liegt. Wie unabhängig einer Lastverteilung aber gewisse Kompensationsbewegungen erfolgen können, die dabei helfen, die Sticking Region zu überbrücken, wurde im obigen Abschnitt aber bereits geschildert. So kann hier sowohl eine im ersten Teil aufgebaute Bewegungsgeschwindigkeit (welche womöglich auch durch eine Schwungbewegung des ganzen Oberkörpers unterstützt wird), als auch durch eine Verringerung des extern wirkenden Hebels erfolgen. Für eine grafische Darstellung ist wie gesagt auf besagten Textabschnitt weiter oben verwiesen.

Von den ellenbogenbeugenden Muskeln des Oberarmes kommen wir nun zu den kniebeugenden Muskeln des Oberschenkels und einer klassischen, liegenden Bein-curl Maschine. Im Grunde ähnelt diese Bewegung dem Bizepscurl relativ stark. Die am Unterschenkel angreifende Last erzeugt im Knie ein Extensions-Drehmoment und verleitet dieses folglich zur Streckung. Um also die Knie entgegen diesen Kräften zu beugen, müssen Beinbeuger-Muskeln ein gegen gesetztes Drehmoment erzeugen. Die Muskelgruppe, um die es hierbei geht, ist die gesamte Beinbeuger- bzw. Hamstring-Gruppe, weil diese ja alle auch über das Knie hinwegziehen. Wenn diese Bewegung nun mit hoher Last oder bis zur Ermüdung ausgeführt wird, dann wird auch hier ersichtlich, dass die Last nicht wirklich von der Hamstring-Gruppe auf andere Muskeln verschoben werden kann, weil diese die wichtigsten und stärksten Beuge-Muskeln im Kniegelenk sind. Anders als im Falle des Bizepscurls mit einer freien Hantel bleibt hierbei, durch den Maschinenaufbau, der Hebelarm der einwirkenden Kraft auf das Rotationszentrum im Knie konstant. Das bedeutet, dass dieser auch nicht verringert werden kann, um dadurch den Widerstand zu reduzieren. Wenn man sich aber die Längenposition der Hamstring-Muskelgruppe im Laufe der Bewegung ansieht, wobei, dadurch, dass die Muskeln teils zweigelenkig sind, Knie- und Hüftgelenke miteinbezogen werden müssen, dann fällt auf, dass sich die Muskeln im Bewegungsabschnitt mit gebeugten Knien, dadurch, dass auch die Hüfte gestreckt ist, in einer sehr kurzen Position befinden. Im Kontext der Muskelmechanik und der Kraftproduktion der Muskel-Sehnen-Einheiten ist dies zugleich eine verhältnismäßig schlechte Position. Daraus folgt, dass in grenznahen Situationen gerade bei zunehmender Kniebeugung eine Kompensationsbewegung stattfinden kann, die daran versucht ist, die zweigelenkigen Muskeln der Hamstring-Gruppe in eine längere Position zu bringen und damit deren Kraft zu erhöhen. Nun stellt man sich natürlich die Frage, wie das in diesem Falle nun bewerkstelligt werden könne. Die Antwort ist recht einfach und wird den meisten Trainierenden auch bereits vertraut sein. Indem nämlich die Hüfte gebeugt und dadurch von der Liegefläche angehoben wird, werden die drei langen Muskeln- bzw. Muskelköpfe der Hamstring-Gruppe seitens der Hüfte nämlich etwas gedehnt. Eine weitere kleine Bewegung, welche unter Umständen ablaufen kann, um zwar nicht signifikant Last von den Hamstrings zu nehmen, diese aber etwas zu unterstützen, ist der Flexionswinkel der Sprunggelenke. Denn auch wenn die Muskeln der Oberschenkelrückseite die wichtigsten und stärksten Knie-beuger sind, sind es nicht die einzigen. Ein anderer großer Muskel, der ebenso über das Kniegelenk hinwegzieht, ist der Gastrocnemius (Zwillingswadenmuskel). Dessen Längenposition wird natürlich von der Bewegung der Sprunggelenke beeinflusst, schließlich ist die Wadenmuskulatur in erster Linie hierfür zuständig. Wenn nun also besagte Beincurl Bewegung mit hoher Last oder bis zur Ermüdung ausgeführt wird und die Bewegung mit maximaler Plantarflexion initiiert wird, dann befindet sich der Gastrocnemius bei gleichzeitig maximal gebeugtem Knie in seiner kürzesten Position. Auch hier kann der Muskel folglich durch eine gewisse Dorsalflexion in eine längere und damit stärkere Position gebracht werden und damit die Agonisten der Bewegung etwas besser unterstützen.

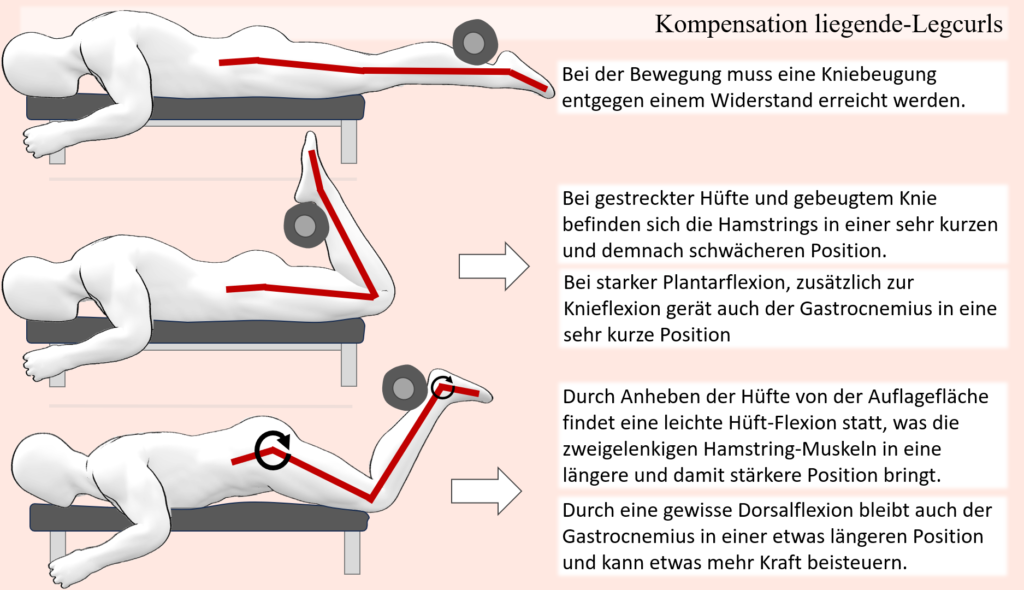
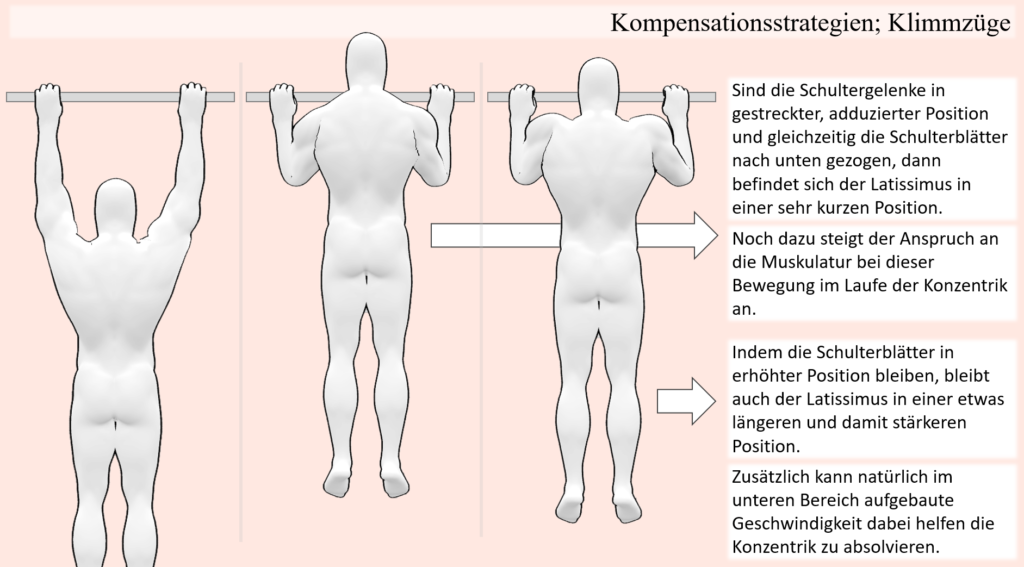
Solche Längenanpassungen durch leichte Bewegungsanpassungen finden sich in vielen Situationen, gerade wenn ein belasteter Muskel im Laufe einer Bewegung in eine sehr kurze Position gerät und eben nicht entlastet werden kann. Ein weiteres sehr anschauliches Beispiel, bei dem es dazu kommen kann und mit welchem darüber hinaus auch die meisten vertraut sein sollten, sind Klimmzüge, oder auch „Pulldowns“ an einem Kabelturm (was in diesem Fall als äquivalent anzusehen ist). Bei dieser Bewegung wird entweder der eigene Körper an fixierten Haltepunkten hochgezogen oder aber eine Stange nach unten gezogen, welche zum Beispiel an einem Kabel befestigt ist, an dessen anderen Ende ein Gewicht als Widerstand befestigt ist. Vom Punkt, an dem die Arme nach oben ausgestreckt sind, findet damit sowohl eine Schulter-Extension als auch Adduktion statt. In diesem Sinne ist der Latissimus auch der wichtigste Agonist für diese Bewegung, wobei dieser von zahlreichen Synergisten in unterschiedlichen Positionen unterstützt wird. Wenn es aber um die Schulter-Extension und Adduktion geht, dann ist der Latissimus der wichtigste Agonist und als solcher auch unersetzbar. Dies lässt schon erahnen, dass auch in diesem Fall keine großartige Entlastung stattfinden kann, wenn der Latissimus an seine Grenzen stößt. Führt man sich andere infrage kommende Muskeln vor Augen, dann wird ersichtlich, dass einige andere Muskeln auch zur Schulter-Extension und Adduktion beitragen können, darunter Muskeln der Rotatorenmanschette, der Teres major oder auch der große Brustmuskel. Dabei erübrigt sich eine eventuelle Lastverschiebung aber, weil jene Muskeln entweder nur als Synergisten in einigen Bereichen der Bewegung gelten oder ihrer Größe wegen gar nicht in der Lage wären, sonderliche Lasten aufzunehmen. Darüber hinaus, wenn es um Muskeln wie dem Teres major geht, der über die ganze Bewegung mit beteiligt ist, dann wären diese Muskeln natürlich bereits mit eingeschlossen, wenn die Bewegung mit hoher Last oder bis zur Ermüdung ausgeführt wird. Betrachtet man nun aber den Latissimus, dann wird auch hier ersichtlich, dass dieser in der obersten Position bei den Klimmzügen oder aber wenn die Stange ganz nach unten gezogen wurde, in der kürzesten Position ist. Nun bedarf die Bewegung an sich aber entsprechender Schulterbewegungen, sprich, wenn das Schultergelenk weniger adduktiert oder gestreckt werden würde, sodass die Fasern des Muskels in einer längeren Position bleiben, dann könnte die Bewegung schlichtweg nicht erfüllt werden. Hier kann nun aber die Beweglichkeit der Schulterblätter zugutekommen, weil hierdurch die ganze Schultergelenkbasis und mitsamt dieser natürlich auch der Oberarm bewegt wird. Wohingegen in einer ausgeruhten Situation, wo z.B. ein Klimmzug ohne großartige Anstrengung ausgeführt werden kann, die Schulterblätter am Beginn bei ausgestreckten Armen in elevierter Position sind und im Laufe der Bewegung mitsamt den Oberarmen nach unten bewegt werden, kann bei hoher Last oder Ermüdung eine elevierte Position der Schulterblätter dafür sorgen, dass die Muskelfasern des Latissimus nicht so stark verkürzen.

Wenn es um mögliche Lastverlagerungen geht, dann geht es im Grunde um die Frage, durch welche Muskeln eine jeweilige Bewegung erzeugt wird bzw. erzeugt werden kann. Kann nun wie im Falle einer Kniebeuge, was erstmal ja nur als die Bewegung vom aufrechten Stand in die Hocke bzw. von der Hocke in den aufrechten Stand definiert wird, diese grobe Bewegung über unterschiedliche Beteiligung von Knie,- Hüft,- und Sprunggelenken ablaufen, dann können entsprechende Muskeln auch unterschiedlich belastet werden. Geht es aber um bestimmte Gelenkbewegungen, dann muss diese in einer offenen kinematischen Kette auch von Muskeln übernommen werden, welche gemäß ihrem anatomischen Verlauf entsprechende Bewegungsfunktionen umfassen. Was vielleicht als selbstverständlich erscheint, wenn man es so liest, sorgt aber tatsächlich vielerorts für Missverständnisse.

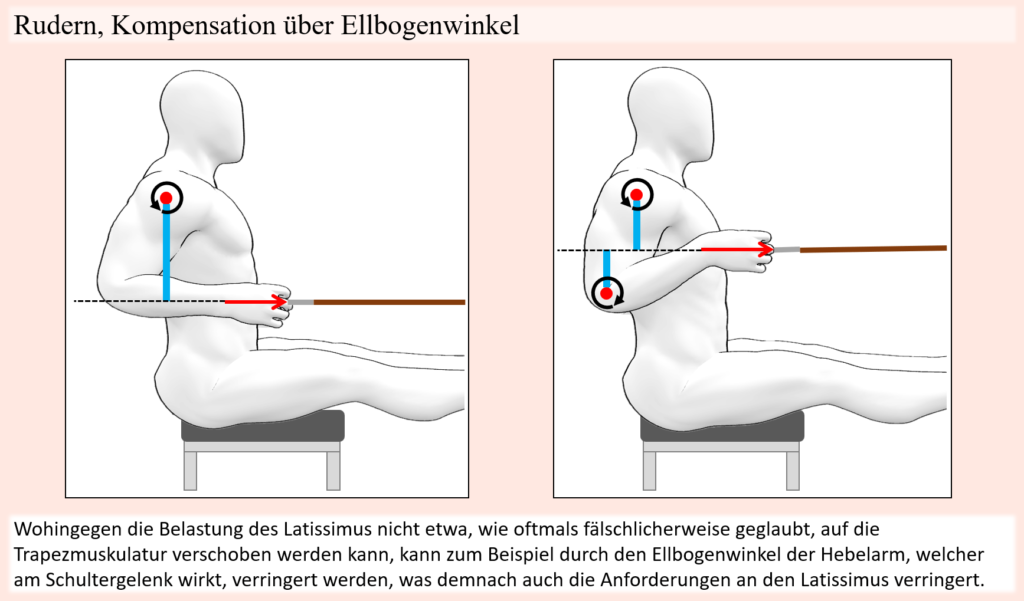
So werden gerade im Breitensport oft gewisse Lastverteilungen postuliert, welche im Grunde rein anatomisch gar nicht möglich sind. Beispielsweise wird oftmals fälschlicherweise behauptet, wenn eine auf den Latissimus ausgelegte Ruder- oder auch Pulldown-Bewegung vermeintlich „unsauber“ ausgeführt wird, dass vermehrt Last zum Beispiel vom Trapezius übernommen wird. Aus anatomischer Sicht, wenn man den Verlauf und ausgehend davon die Bewegungsfunktionen des Latissimus und des Trapezius aber vergleicht, dann wird schnell klar, dass dies nicht wirklich sein kann, wenn wir von einer langsamen Bewegungsausführung ausgehen. Schließlich zieht der Trapez überhaupt nicht über das Glenohumeralgelenk (Schultergelenk), weswegen der Trapez überhaupt nicht dazu befähigt ist, die Bewegung des Oberarmes zu übernehmen, sodass der Latissimus entlastet werden würde. Eine Möglichkeit, wie hingegen der Latisimus unter Umständen mit etwas weniger Widerstand konfrontiert werden könnte, ist durch vermehrte Involvierung des Bizeps, wodurch die Wirkungskraftlinie, welche an den Händen angreift, womöglich näher am Schultergelenk verläuft.

Ein ähnliches Missverständnis wird zum Beispiel auch im Kontext des Seithebens mit Kurzhanteln oftmals angenommen. Nämlich dass hierbei auch wieder vermehrt Last vom seitlichen Delta-Muskel auf den oberen Trapezius verlagert werden würde, wenn jene Bewegung „unsauber“ ausgeführt wird. Doch auch hier, der Trapezius ist überhaupt nicht dazu in der Lage, dieBewegungsfunktion des seitlichen Deltas, nämlich in diesem Fall die Abduktion des Armes, zu übernehmen. Vielmehr könnte die Kontraktion der oberen Trapez-Fasern genutzt werden, um Schwung aufzubauen, sodass die Abduktionsbewegung, welche im Falle von Kurzhanteln am anspruchsvollsten bei horizontal abduzierten Armen ist, weiterhin ausgeführt werden kann, auch wenn dies ohne diesen Impuls nicht mehr möglich wäre.

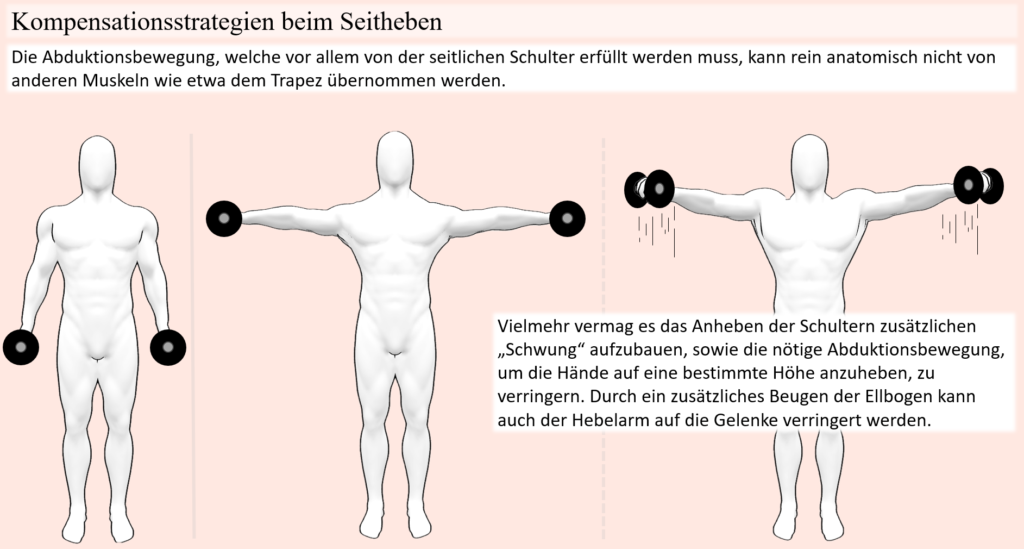
Insofern also nicht die Bewegung des Gelenkes selbst verändert wird, sodass vermehrt andere Muskeln mit entsprechenden Funktionen hierfür zuständig sind, kann ein zuständiger Muskel also auch nicht einfach so entlastet werden. Was natürlich nicht bedeutet, dass nicht andere Muskeln zusätzlich aktiv sein können. Werden bei besagter Ruder-Bewegung also die Schulterblätter im Laufe der Bewegung nach vorne geführt und wieder zusammengezogen, oder aber im Falle des Seithebens die Schultern, zusätzlich zu der Abduktionsbewegung der Arme, angehoben, dann sind diese Bewegungen wiederum auf Muskeln zurückzuführen, welche jene Bewegungsfunktionen erfüllen. Wenn es nun aber um eine Bewegung geht, deren Ziel auf mehreren Wegen erreicht werden kann und nicht auf einer bestimmten Gelenkbewegung basiert, zum Beispiel dem Aufstehen von einem Stuhl, dann kann die Gesamtbewegung, die das Ziel hat von der sitzenden Position in den aufrechten Stand zu kommen, eben durch unterschiedliche Beteiligung der einzelnen dabei belasteten Gelenke ablaufen. Ebenso kann die Lastverteilung auf diese Gelenke durch deren Abstand zur Schwerelinie variiert werden. Dies verschafft die Möglichkeit vom Stuhl aufzustehen und dabei zum Beispiel den Quadrizeps relativ wenig zu Belasten und im Gegenzug die Hüftstrecker umso mehr, oder auch umgekehrt.

Damit haben wir zugleich auch schon einen passenden Übergang zur Betrachtung einer Kniebeuge, samt Kompensationsbewegungen, welche, je nachdem welcher der beteiligten Muskelgruppen entlastet werden muss, aufkommen können.

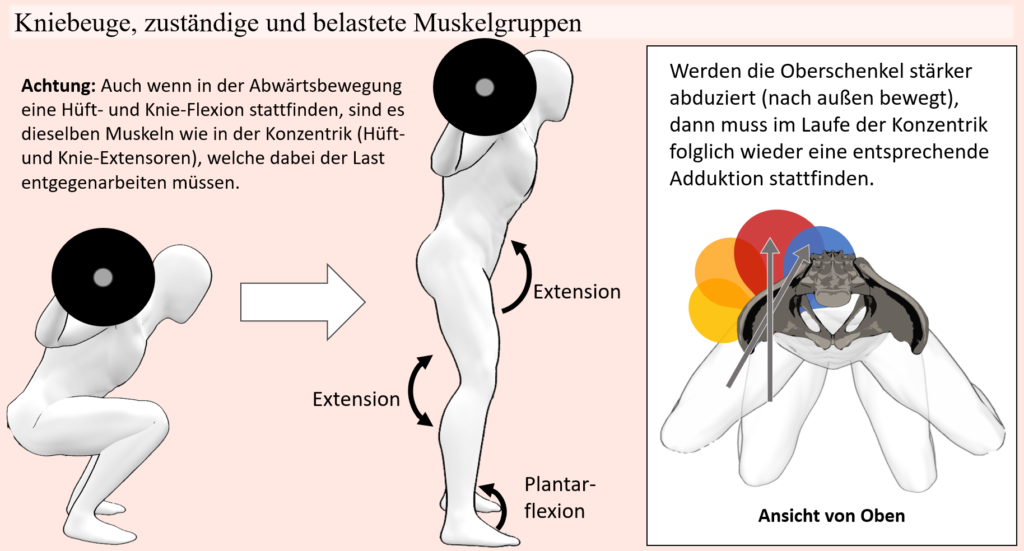
Kniebeuge, Bewegung und zuständige Muskeln

Die Kniebeuge ist der aufsteh-Bewegung von einem Stuhl natürlich sehr ähnlich. Im Allgemeinen beschreibt sie wie gesagt lediglich die Bewegung aus der Hocke in den aufrechten Stand und vice versa. Das allein ist aber noch keine ausreichende Beschreibung der Bewegung, um ausgehend hiervon die Muskelbeteiligung, geschweige denn die jeweiligen mechanischen Begebenheiten abzuleiten. Dementsprechend gilt es diese grobe Definition zu spezifizieren, indem die belasteten Gelenke identifiziert werden, ebenso wie deren jeweilige Bewegung im Laufe der Gesamtbewegung. In diesem Sinne kann man schon mal grob festhalten, dass besagte „Hocke“ eine Position ist, in der eine Hüft-Knie- und Dorsalflexion vorhanden ist. Um von hier aus in den aufrechten Stand zu gelangen, muss dementsprechend eine Hüft- sowie Knie-Extension stattfinden, als auch eine Plantar Flexion, die damit einhergeht. Unter Umständen, genauer gesagt je nach Standbreite kann dabei auch noch eine gewisse Hüft-Adduktion mit dabei sein. Vom aufrechten Stand in die Hocke und wieder zurück beinhaltet also eine Hüft-Flexion/Extension, Knie-Flexion/Extension, Dorsalflexion/Plantar-Flexion und eine gewisse Hüft-Abduktion/Adduktion. Daraus ergeben sich jeweilige Muskeln und Muskelgruppen, welche für jene Bewegungsfunktionen zuständig sind. Bezieht man nun die Last bzw. den Widerstand mit ein, der im Laufe der Bewegung überwunden bzw. standgehalten werden muss, dann wird ersichtlich, dass die exzentrische Bewegungsphase, welche eine Hüftflexion, Hüftabduktion, Knieflexion und Dorsalflexion, mit einschließt, nicht seitens der Muskulatur erzeugt werden muss, weil die Last entsprechende Gelenkbewegungen erzeugt. Dementsprechend ist die Aufgabe der Muskulatur in jener Bewegungsphase, die Last abzubremsen und von ihr erzeugte Gelenkdrehmomente abzuschwächen. Das wiederum muss aber durch entgegengesetzte Muskelkräfte bzw. muskuläre Drehmomente geschehen, woraus folgt, dass auch beim Ablassen vom aufrechten Stand in die Hocke, wo zum Beispiel eine Knieflexion stattfindet, nicht etwa die kniebeugende Muskulatur jene Flexion auslöst, sondern vielmehr die Kniestrecker Kraft erzeugen müssen um den „Flexions-Drehmomenten“, welche die Last erzeugt, entgegenzuwirken. Selbes gilt auch seitens der Hüftgelenke, wo nicht die hüftbeugende Muskulatur diese Bewegung leitet, sondern vielmehr die Hüftstrecker. Für die konzentrische Bewegungsphase wiederum, wo vor allem eine Hüft- und Knie-Streckung entgegen der Last ausgeführt werden, ist offensichtlich, dass hierfür entsprechend Hüft- und Kniestrecker verantwortlich sind. Die Unterschenkelmuskeln, sprich Plantar-Flexoren sind in dieser Bewegung tatsächlich hauptsächlich als Stabilisatoren für die Aufrechterhaltung des Gleichgewichtes beteiligt und nur zum Teil für die aktive Plantarflexion. Warum das so ist, wird etwas weiter unten ersichtlicher, wenn es um die hier anzutreffende spezielle Rolle biartikulärer Muskeln geht.

Damit hätten wir die Agonisten der Bewegung, nämlich zum einen die Hüftstrecker und zum anderen die Kniestrecker. Letztere können wir im Quadrizeps zusammenfassen, der seinerseits aus vier einzelnen Muskeln, oder wenn man so will, Muskelköpfen, zusammengesetzt ist. Darunter der Vastus lateralis, Vastus medialis, Vastus intermedius sowie der Rectus femoris. Bis auf den Rectus femoris, entspringen die Quadrizepsmuskeln am Oberschenkelknochen und verlaufen mittels der Quadrizepssehne, welche wiederum in die Patellasehne übergeht, zusammen. Dadurch, dass die Quadrizepsmuskeln die einzigen Kniestrecker sind, sind es auch jene Muskeln, die durch den gesamten Bewegungsumfang des Knies für die Extension, bzw. die kontrollierte Flexion in der exzentrischen Bewegungsphase, verantwortlich sind. Der Rectus femoris zieht dabei als einziger auch über das Hüftgelenk, wo er zur Flexion beiträgt. Wie gesagt erfolgt bei einer Kniebeuge keine von den Hüftbeugern geführte Hüftbeugung, sondern vielmehr müssen die Hüftstrecker der von der Last erzeugten Hüftbeugung entgegenwirken. Aus diesem Grund ist der Rectus femoris auch jener Quadrizepsmuskel, welcher durch seine übermäßige Kontraktion die Zielbewegung sogar beeinträchtigen kann, weil er seitens der Hüfte der Extension mehr Widerstand entgegenstellt.

Was die Hüfte, bzw. die Hüftstreckung anbelangt, gilt der Gluteus maximus als stärkster und wichtigster Hüftstrecker. Entsprechend ist er auch bei der Kniebeuge vor allem dafür verantwortlich. Im Gegensatz zum Kniegelenk, wo der Quadrizeps der einzige Strecker ist, stehen dem Gluteus maximus aber andere Muskeln als Unterstützung zur Seite, so vor allem die Hamstring-Gruppe, teilweise der Adduktor Magnus als auch bis zu einem gewissen Grad natürlich seine kleineren Namensvetter. Dies kommt dem Gluteus maximus natürlich auch zugute, schließlich verliert er mit zunehmender Hüftflexion an Hebelarmlänge, weswegen die von ihm erzeugten „Extensions-Drehmomente“ in den Hüftgelenken im Verhältnis abnehmen. Praktischerweise nehmen die Hebelarme und damit deren Auswirkung auf die Hüftstreckung von anderen Muskeln, nämlich vom Adduktor Magnus als auch der Hamstring-Gruppe bei Hüftflexion zunächst zu. Dementsprechend kann gerade in Bereichen der Kniebeuge mit starker Flexion in den Hüftgelenken auch etwas mehr Belastung vom Adduktor Magnus und teilweise den Hamstring-Muskeln übernommen werden. Die Involvierung des Adduktor Magnus kann dabei vor allem auch durch die Standbreite beeinflusst werden, was durch seine Zugrichtung und Bewegungsfunktion ersichtlich wird. Werden durch einen breiten Stand die Oberschenkel stark nach außen bewegt, dann folgt in der konzentrischen Bewegungsphase wieder eine Adduktion. Wird die Kniebeuge mit schmalem Stand ausgeführt (Oberschenkel bleiben im Laufe der Bewegung nahe aneinander), so entspricht der Bewegungspfad des Oberschenkels weniger der Zugrichtung des Adduktor Magnus. Ähnlich wie im Falle der Kniestreckung haben wir nun aber auch hier einen Muskel, bzw. in diesem Fall eine Muskelgruppe, welche nicht nur über das Hüftgelenk, sondern eben auch über das Kniegelenk hinwegzieht. Die Rede ist natürlich von der Hamstring-Gruppe. Und wie auch im Falle des Rectus femoris, kann auch hier diese Muskelgruppe die Kniebeuge durch die Funktion als Hüftstrecker unterstützen, andererseits unterstützen jene Muskeln an den Knien aber eine Flexion und stehen damit der Kniestreckung entgegen. Wie gesagt, auch bei der Abwärtsbewegung müssen die Knie-Flexoren keine Beugung verursachen, sondern die Extensoren müssen diese kontrollieren. Dementsprechend kann der Kraftaufbau der Hamstring-Gruppe seitens der Knie auch wieder die eigentliche Zielbewegung beeinträchtigen, weil der Widerstand, welcher den Extensoren (Quadrizeps) entgegensteht erhöht wird.

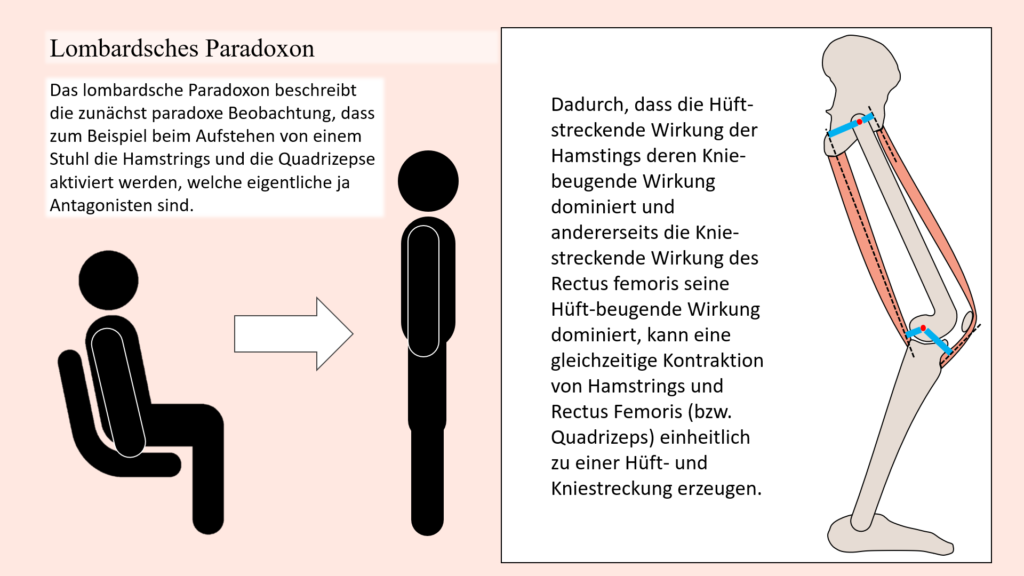
Lombardsches Paradoxon

Das sogenannte lombardsche Paradoxon basiert auf einer vom Standpunkt der klassischen anatomischen Funktionszuschreibung scheinbar paradoxen Funktion der ischiocruralen Muskulatur (Hamstrings) beim Menschen. Betrachtet man einen Skelettmuskel, dann schließt man im Allgemeinen von seinem Verlauf auf die jeweilige Bewegungsfunktion, welche durch eine Kontraktion des entsprechenden Muskels erzeugt wird. Nun hat sich aber gezeigt, dass solch eine isolierte Betrachtung nicht immer realitätskonform ist, wenn Muskeln scheinbar Bewegungen unterstützen, welche sogar gegensätzlich zu ihrer klassischen Funktion sind. Wenn ein Muskel also aktiv ist und am beteiligten Gelenk zum Beispiel als Flexor funktioniert, die resultierenden Drehmomente aber gleichzeitig eine extensorische Wirkung aufweisen, dann wirkt dieser Muskel paradox. Im Falle des lombardschen Paradoxons wird die „Paradoxie“ dementsprechend darin gesehen, dass bei Fixierung des Fußes und des Beckens die ischiocrurale Muskulatur zur Streckung des Kniegelenks beiträgt. Das Phänomen wurde bereits Anfang des 20. Jahrhunderts vom US-amerikanischen Physiologen Lombard beschrieben, wonach es schließlich auch benannt wurde.

Das Paradoxon lässt sich aber erklären, wenn man nicht nur den Muskel und dessen Verlauf isoliert betrachtet, sondern vielmehr die mechanischen Begebenheiten des Bewegungsapparates bei der entsprechenden Bewegung. Im Kontext der kinematischen Ketten, genauer gesagt speziell bei geschlossenen kinematischen Ketten haben wir ja bereits gesehen, dass Muskeln Gelenke beeinflussen und Gelenkbewegungen verursachen können, mit denen sie isoliert betrachtet, gemäß ihrem anatomischen Verlauf eigentlich nichts zu tun haben. In diesem Sinne wurde bereits aufgezeigt, dass wenn Becken und Füße fixiert sind und somit eine geschlossene Bewegungskette vorhanden ist, dass dann eine Hüftstreckung ebenso eine Kniestreckung verursacht, genauso wie umgekehrt eine Kniestreckung ebenso eine Hüftstreckung verursacht. Wenn man sich nun die klassischen Funktionsbereiche der ischiocruralen Muskulatur ansieht, dann fällt auf, dass diese Muskulatur im Hüftgelenk eine Streckung, also Extension erzeugt und im Kniegelenk eine Beugung. Wenn wir uns nun eine geschlossene Bewegungskette wie in einer Beinpresse vorstellen, dann wird aber ersichtlich, dass diese Hüftstreckung und die Kniebeugung gegensätzliche Aktionen sind, denn um die Hüfte zu strecken müssen auch die Knie gestreckt werden. Wenn man sich also einen Bewegungsapparat vorstellt, wo die einzig wirkenden Muskelkräfte jene der ischiocruralen Muskulatur sind, dann kommt die letztendliche Bewegung darauf an, an welchem Gelenk die Muskulatur ein stärkeres Drehmoment erzeugt. Weil Muskeln in ihren verschiedenen Teilen keine unterschiedliche Kraft entwickeln können, kommt dies wiederum auf die gegenwärtigen Hebelarme an. Überwiegt letztlich die Streckwirkung an der Hüfte gegenüber der Beugewirkung am Knie, dann unterstützen die Hamstrings in einer geschlossenen Kette die Kniestreckung.

Aber das ist nicht alles. Vielmehr ermöglichen es zweigelenkige Muskeln wie die Hamstrings auch unabhängig einer geschlossenen kinematischen Kette Kräfte von einem Gelenk auf das andere zu übertragen. Eingelenkige Muskeln bewegen ausschließlich ein Gelenk (außer es handelt sich um eine geschlossene kinematische Kette). Daraus folgt, dass die gegenwärtigen Eigenschaften eingelenkiger Muskeln, wie z. B. die Längenposition (und folglich die Längen-Kraft-Relation) direkt über die jeweilige Gelenkstellung ermittelt werden kann. Nun würde ein komplexer Bewegungsapparat wie der unseres Körpers eine enorme Steuerungs- und Kontrollleistung des Gehirns erfordern, wenn alle Gelenke vollkommen unabhängig voneinander durch entsprechende Muskeln kontrolliert und koordiniert werden müssten. Zweigelenkige Muskeln sind hingegen in der Lage, Kräfte von unterschiedlichen Gelenken auf andere Gelenke zu übertragen und zum Beispiel die im Hüft- und Kniegelenk erzeugten Kräfte auf das Sprunggelenk zu transferieren, ohne dabei selbst aktiv zu sein. Auch können Kräfte von Knie zu Hüfte bzw. Hüfte zu Knie weitergeleitet werden, wodurch eingelenkige Muskeln der jeweiligen Gelenke demnach nicht mehr sämtliche Kräfte allein bereitstellen müssen, sondern ein gewisser Anteil, von einem anderen Gelenk durch einen zweigelenkigen Muskel zur Verfügung gestellt wird.

Im Sinne des lombardschen Paradoxons, welches sich um Knie- und Hüftgelenke dreht, ist die ischiocrurale Muskulatur offensichtlich zweigelenkig, was bereits erahnen lässt, dass hier eben genau sowas stattfindet. Etwas genauer betrachtet wird nun aber auch schnell auffallen, dass neben den Hamstrings, auf der Vorderseite des Oberschenkels ein weiterer Muskel vorhanden ist, welcher über Hüfte und Knie zieht und jeweils gegensätzliche Bewegungsfunktionen erfüllt. Die Rede dabei ist vom Rectus femoris, welcher isoliert betrachtet am Kniegelenk eine Streckung und am Hüftgelenk eine Beugung erzeugt. Das Paradoxon lässt sich nun durch die relativen Hebelarme der Hamstrings und des Rectus femoris an den Hüft- und Kniegelenken und den Auswirkungen auf die Größe der jeweiligen Drehmomente, die von jeder Muskelgruppe an jedem der beiden Gelenke erzeugt werden, erklären. Wie gesagt, Muskeln können in ihren verschiedenen Teilen keine unterschiedliche Kraft entwickeln. Die hintere Oberschenkelmuskulatur kann beispielsweise die Hüfte nicht gezielt strecken, ohne mit gleicher Kraft auf das Knie einzuwirken. Die einzige Möglichkeit, dass Hüft- und Kniestreckung gleichzeitig (zum Beispiel beim Aufstehen) erfolgen können, besteht darin, dass das Nettodrehmoment sowohl am Hüft- als auch am Kniegelenk ein Streckmoment ist, auch wenn antagonistische Muskeln gleichzeitig Streck- und Beugemomente entwickeln. Dabei ist es lediglich erforderlich, dass das Drehmoment der Strecker das Drehmoment der Beuger übersteigt. Zwei antagonistische Muskeln können ein solches Nettodrehmoment erzeugen, selbst wenn sie identische Kräfte entwickeln, wenn ihre Hebelarme um die Gelenke ungleich sind. Der Rectus femoris, der über die Hüfte wirkt, hat einen kleineren Hüft-Hebelarm als die hintere Oberschenkelmuskulatur. Allerdings ist der Hebelarm des Rectus femoris am Knie größer als der Hebelarm der Hamstrings. Dies bedeutet, dass die Kontraktion sowohl des Rectus femoris als auch der hinteren Oberschenkelmuskulatur zu einer Streckung der Hüfte und des Knies führt und das erklärt, warum die Aktivität der ischiocruralen Muskulatur beim Springen, Aufstehen oder eben auch bei einer Kniebeuge nicht gleich auch konträr zur eigentlichen Bewegung ist (solange die Beuge-Wirkung nicht die Streck-Wirkung übersteigt).

Diese Funktionsweise partikulärer Muskeln sorgt nun dafür, dass auch eingelenkige Muskeln, welche isoliert betrachtet nur ein Gelenk beeinflussen können, über biartikuläre Muskeln nun eben auch andere Gelenke beeinflussen können. Hier kommen wir dann auch zur weiter oben bereits angedeuteten Beteiligung der Wadenmuskulatur in einer Kniebeuge- oder auch Sprung-Bewegung. Denn obwohl die Sprunggelenke im Laufe solcher Bewegungen offensichtlich aktiv bewegt werden müssen, sprich in der exzentrischen Bewegungsphase neben Hüft- und Kniebeugung eben auch zwangsweise eine Dorsalflexion stattfinden muss, sowie im konzentrischen Teil dann wiederum eine Plantarflexion, wird diese Bewegung nur zum Teil durch die Aktivität der Wadenmuskulatur verursacht. In Anbetracht der zweigelenkigen Muskeln und was diese ermöglichen, macht dies aber durchaus Sinn. So ist einer der zwei großen Plantarflexoren, nämlich der Gastrocnemius, ein zweigelenkiger Muskel, welcher nicht nur über das Sprunggelenk, sondern eben auch über das Kniegelenk zieht. Das wiederum bedeutet, dass er auch von der Stellung des Kniegelenkes und damit von Muskeln, welche dieses vorwiegend kontrollieren, beeinflusst wird. Im Falle einer Sprung-Bewegung oder eben auch einer Kniebeuge geht es hierbei vor allem um den Quadrizeps. Isoliert betrachtet hat der Quadrizeps offensichtlich nichts mit dem Fußgelenk zu schaffen und würde man auch nur den Quadrizeps isoliert bei einer offenen kinematischen Bewegungskette betrachten, dann hätte seine Kontraktion auch keine Auswirkung auf das Fußgelenk. Im Kontext des Gastrocnemius kann nun aber Kraft vom Knie auf das Sprunggelenk übertragen werden. Da die Quadrizepse das Knie strecken, würde sich der Gastrocnemius leicht dehnen, wenn er entspannt wäre. Diese leichte Dehnung könnte nun bereits eine geringe Kraft auf das Sprunggelenk übertragen. Bleibt nun aber die Länge des Gastrocnemius gleich oder verkürzt sich sogar, wird die sonst durch die Kniestreckung entstehende Dehnung stattdessen auf den Knöchel übertragen, wo sie die kräftige Plantarflexion unterstützt. Mit anderen Worten, der Quadrizeps fungiert eben durch den Gastrocnemius, welcher die Kraftübertragung ermöglicht, als Plantar-Flexor.

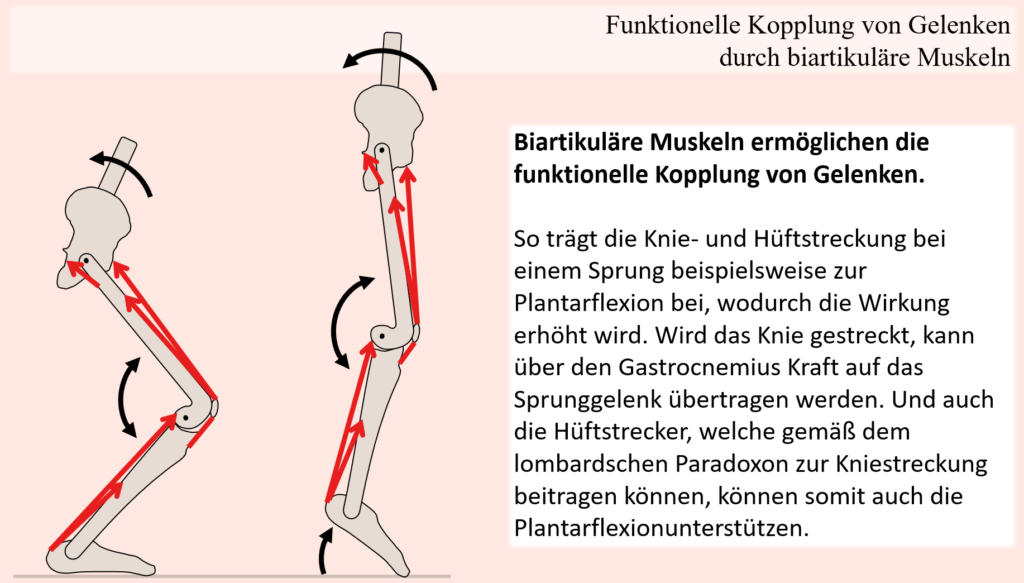
Aber das ist nicht alles. Wir haben ja bereits gesehen, dass sich zwischen Knie und Hüfte vor allem zwei biartikuläre Muskeln bzw. Muskelgruppen aufspannen, nämlich die ischiocrurale Muskulatur, welche isoliert betrachtet das Knie beugt und die Hüfte streckt, als auch der Rectus femoris welcher isoliert betrachtet die Hüfte beugt und das Knie streckt. Auch in diesem Fall ermöglichen es jene zweigelenkigen Muskeln Kraft vom einen auf das andere Gelenk zu übertragen, oder auf den Punkt gebracht, der Quadrizeps unterstützt die Hüftstreckung und der Gluteus (stellvertretend für die Hüft-Strecker) unterstützt die Kniestreckung. Isoliert betrachtet scheint es absurd den Gluteus als Kniestrecker und den Quadrizeps als Hüftstrecker zu bezeichnen, im Kontext der zweigelenkigen Muskeln ergibt es aber durchaus Sinn. Das Prinzip bleibt dabei dasselbe wie auch im Falle der Plantarflexion. Solange sich also der Rectus femoris während der konzentrischen Phase der Kniebeuge nicht tatsächlich verlängert, wird das Drehmoment der Hüftstreckung auf den Rectus femoris übertragen, was zu einer Kniestreckung führt. Und insofern die Hamstring-Gruppe nicht gedehnt wird, führt die Kniestreckung durch dasselbe Prinzip auch zu einer Hüftstreckung. Damit trägt übrigens dann auch die Hüftstreckung letztendlich zur Plantarflexion bei, weswegen nicht nur der Quadrizeps, sondern auch der Gluteus in diesem Kontext als Plantarflexor bezeichnet werden kann.

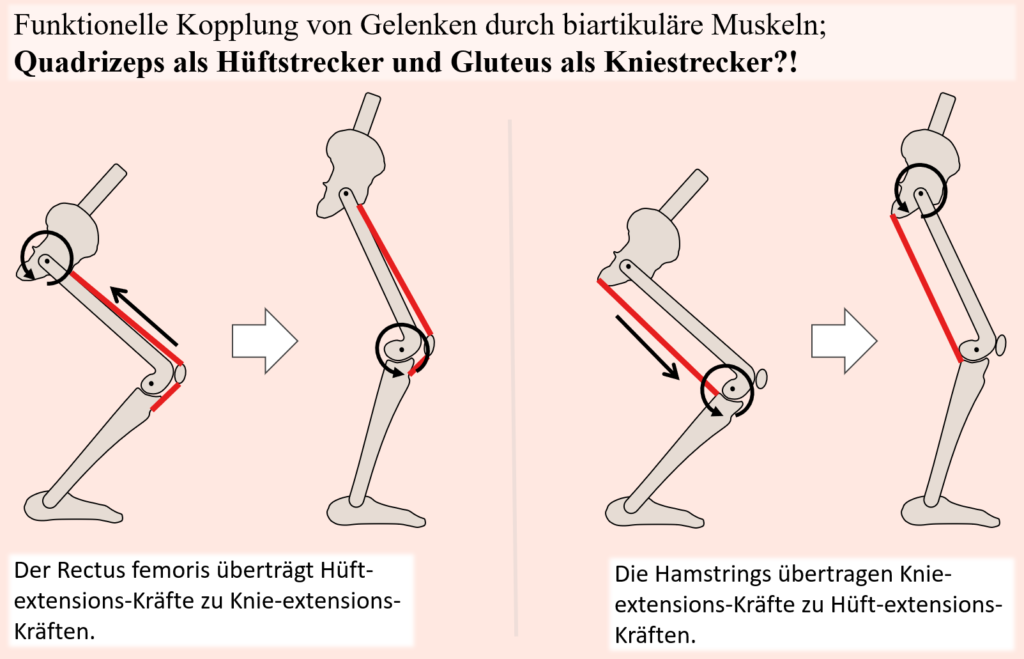
Wohlgemerkt ist diese Funktion biartikulärer Muskeln ein weiterer Faktor, weshalb durch alleinige Betrachtung von einwirkenden Kräften, deren Hebelarme auf belastete Gelenke und den jeweiligen Gelenkbewegungen nicht exakt auf die muskuläre Beteiligung geschlossen werden kann, bzw. kleinere Änderungen der Bewegungsausführung eben nicht gleichzeitig auch zulassen, entsprechende Vorhersagen der exakten muskulären Beteiligung zu machen.

Kompensationsstrategien in der Kniebeuge

Auch wenn uns einige unbekannte Variablen die Möglichkeit abschlagen, exakte biomechanische Vorhersagen bei jeweiligen Bewegungen zu treffen, so korreliert die Belastung der jeweiligen Muskeln zumindest grob mit den Drehkräften, welche die Last in den jeweiligen Gelenken erzeugt. Ist der gegenwärtige Hebelarm in einer bestimmten Situation der Kniebeuge sehr groß auf das Hüftgelenk, wohingegen der Hebelarm auf das Kniegelenk klein ausfällt, dann kann man davon ausgehen, dass auch die Hüftmuskulatur den Großteil der Last tragen muss. Und genau hier kommen wie gesagt Kompensationsbewegungen ins Spiel, bei welchen der Körper über Lastverschiebung die zu bewältigende Last unterschiedlich aufteilen kann, wodurch jeweilige muskuläre Schwächen eben kompensiert werden können. Im Folgenden sehen wir uns dementsprechend beispielhaft solche Kompensationsbewegungen anhand von einigen Bildern an (teils Frames aus Videoanalysen samt Bewegungsverfolgung, teils stellvertretend dafür angefertigte Grafiken) und versuchen anhand der dargestellten Ausweichbewegungen darauf zu schließen, welche Muskeln eher entlastet und welche stärker belastet werden.

Als Wirkungskraftlinie dient uns hierbei (bei der Kniebeuge) die Schwerelinie. Dabei ist wichtig zu beachten, dass diese Schwerelinie nicht einfach von der Hantel ausgeht, sondern vom Massenschwerpunkt, welcher sowohl die Masse des Athleten als auch der Hantel mit einschließt. Dies führt dazu, dass die Hantel sich aus sagittal betrachtet, vor allem wenn diese im Verhältnis zum Körpergewicht gering ausfällt, durchaus von der Schwerelinie entfernen kann, bzw. dies unter Umständen sogar muss, damit der Schwerpunkt über dem Mittelfuß gehalten und so eine stabile Standposition aufrechterhalten werden kann. Dies zeigt sich auch in einigen der Frames, welche in den Beispielen unten zum Vorzeigen bestimmter Kompensationen verwendet werden. Entsprechende Kompensationen wurden nachgestellt und hierzu wurde die Hantel im Verhältnis zum Gewicht des Athleten nur recht leicht beladen. Aus diesem Grund zeigt sich an einigen Stellen deutlich, dass der Hantelpfad leicht nach vorne wandert, auch wenn der Schwerpunkt die ganze Zeit über dem Mittelfuß liegt. Je schwerer die Hantel im Verhältnis zum Körpergewicht ist, desto genauer stimmt der Hantel Pfad auch mit dem Schwerpunkt überein. Dementsprechend wird die Verfolgung des Hantelpfades auch erst dann richtig interessant, weswegen in den unteren Beispielen zu verschiedenen Kompensationsbewegungen in der Kniebeuge das Hauptaugenmerk auf dem Hüft-Pfad liegt. Bevor wir nun aber dazu kommen, gilt es zunächst Aspekte einer optimalen Kniebeuge zu betrachten, um folglich zu sehen, wie entsprechende Kompensationen davon abweichen.

Wichtige Aspekte für die mechanisch optimale Kniebeuge

Auch wenn die letztendliche Optik einer Kniebeuge sich von Mensch zu Mensch unterscheiden kann, so gibt es durchaus eine Handvoll von Aspekten, welche unabhängig dessen eine mechanisch vorteilhafte Kniebeuge ausmachen. So ist die absolute Grundlage dafür, überhaupt eine freie Kniebeuge ausführen zu können, das Gleichgewicht. Dieses kann nur erhalten werden, wenn sich der Schwerpunkt oberhalb der Unterstützungsfläche der Füße befindet. Ist dies nicht der Fall, dann fällt man um. Der Schwerpunkt entspricht dabei dem Massenschwerpunkt, welcher sich aus der Masse der Hantel und des Körpers ergibt, was ebenso bedeutet, dass eben nicht die Hantel sich stets über dem Mittelfuß befinden sollte, sondern der Schwerpunkt (je schwerer die Hantel, desto ähnlicher wird dies aber natürlich). Ebenso unabhängig vom genauen Bewegungspfad deutet ein gleichbleibender Pfad in Konzentrik und Exzentrik darauf hin, dass in der konzentrischen Bewegungsphase kein schwächelnder Muskel kompensiert werden musste. Ebenso sollte die Wirbelsäule bzw. der Rücken in einer starren Position stabilisiert werden, schließlich dient dieser als Lastleiter, also Kräfte möglichst 1 zu 1 von A nach B weiterzugeben. Gibt die Wirbelsäule hingegen nach, dann verpuffen Kräfte sozusagen in dieser Bewegung. Und zu guter Letzt ist es ebenso vorteilhaft, wenn sich Knie- und Hüfte im Laufe der Bewegung einigermaßen simultan bewegen. Wird eines der beiden Gelenke nämlich verhältnismäßig schneller oder aber alleine rotiert, hat dies oftmals Lastverschiebungen zur Folge, wodurch bestimmte Muskeln entlastet und andere vermehrt belastet werden.

Entlastung der Kniestrecker

Die zwei großen Agonisten-Muskelgruppen der Kniebeuge sind zum einen die Kniestrecker und zum anderen die Hüftstrecker, weswegen sehr viele Kompensationsstrategien darauf zurückgehen, dass einer dieser Muskeln die ihnen auferlegte Last nicht bewältigen kann. Wohl eine der häufigsten Ausweichbewegungen beläuft sich dabei auf eine Entlastung der Quadrizepse. Auf solch eine Lastverschiebung werden wir in mehreren Beispielen treffen, wobei es aber immer darum geht, dass die Hebelarme der Wirkungskraftlinie auf die Knie verringert werden, was zum einen wie gesagt bedeutet, dass der Kniestreckung weniger Widerstand gegenübersteht, gleichzeitig andere Strukturen aber mehr Last tragen müssen. Bei einer klassischen Hüftstrecker-dominanten Kniebeuge zeigt sich so also aus sagittal betrachtet zum Beispiel im Laufe der Bewegung eine Annäherung der Schwerelinie an die Knie, sodass die dort wirkenden Hebelarme abnehmen. Gleichermaßen nimmt der Normalabstand zu den Hüftgelenken aber zu, weswegen den Hüftstreckern ein entsprechend höherer Widerstand entgegensteht. Wann genau im Laufe der Bewegung diese Entlastung stattfindet, kann unterschiedlich sein. Klassischerweise ist dies vor allem im ersten Bewegungsabschnitt der Konzentrik aber sehr offensichtlich, selbst ohne Bewegungsverfolgung. Dies macht natürlich auch Sinn, denn zum einen müssen die Muskeln, also so auch die Quadrizepse, in der konzentrischen Bewegungsphase den Widerstand nicht nur abbremsen, so wie in der Exzentrik, sondern ihn überwinden. Ebenso steigen die Hebelarme der Last auf die Knie bis zum Punkt, an welchem die Oberschenkel horizontal zum Boden sind, stark an, was bedeutet, dass in diesen tiefen Positionen dementsprechend auch die Quadrizepse, als Kniestrecker stark gefordert werden. Können sie diesen Anforderungen nicht gerecht werden, dann müssen sie entlastet werden, indem andere Muskeln, sprich die Hüftstrecker zur Hilfe kommen. Die Hüfte schießt folglich beim Aufstehen nach hinten, dabei kippt der Oberkörper nach vorne. Im Extremfall resultiert dies in einer sogenannten „Good Morning“ Kniebeuge, welche zum Großteil nur noch in einer Hüftstreckung besteht. Wird die Hüfte von der Schwerelinie wegbewegt, nähern sich die Knie an, wodurch es einfacher fällt diese zu strecken. Nun liegt der Großteil der Last aber auf den Hüftstreckern. Gerade weil der Gluteus maximus bei starker Hüftflexion nun aber einen verhältnismäßig kurzen Hebelarm, auf das die Hüftgelenke hat, können vor allem auch die Hamstrings, welche durch die gebeugte Hüfte und die gestreckten Knie in eine lange Position versetzt wurden, etwas Aushilfe bieten, wobei deren Beitrag gewissermaßen als zweischneidiges Schwert zu betrachten ist, weil sie Seitens der Knie dann auch zu einem größeren Widerstand für die Streckung führen können.

In einigen Fällen kann es auch bereits in der exzentrischen Bewegungsphase zu einer mäßigen Schwerpunktverlagerung nach vorne kommen, mit dem Ziel den Widerstand in den Knien zu verringern.

Entlastung der Hüftstrecker

Das Gegenteil der vorher beschriebenen Ausweichbewegung, also einer Entlastung der Kniestrecker, ist eine Entlastung der Hüftstrecker. Auch dies findet sich in mehreren der unteren aufgezeigten Kompensationsbewegungen. Zum Teil geht es dabei schlichtweg um eine Lastverschiebung auf die Kniestrecker, oftmals, wie in den zwei folgenden Beispielen ersichtlich wird, aber auch um eine Lastverschiebung innerhalb der Hüftstrecker, wobei bestimmte Hüftstrecker-Muskeln vermehrt belastet werden. Zunächst bleiben wir aber bei der schlichten Entlastung der gesamten Hüftstrecker, durch die Annäherung der Hüfte an die Schwerelinie. Wie auch im obigen Beispiel hat diese Annäherung zur Folge, dass die Hebelarme auf die (Hüft-) Gelenke und damit gleichzeitig die Anforderungen an die Muskeln reduziert werden. Gleichzeitig werden hier jetzt aber die Knie von der Schwerelinie entfernt, sodass der Widerstand für die Kniestreckung ansteigt. Solch eine Kompensationsstrategie ist wohl deutlich seltener, zumindest wenn es um eine einheitliche Lastverschiebung auf die Knie und nicht etwa einem „hin und her“ wie in einem anderen der unteren Beispiele geht. Wo man solch eine Kompensationsstrategie aber durchaus antreffen kann, ist vor allem in Fällen, wo die Bewegung zwangsweise relativ kniedominant ausgeführt werden muss. So zum Beispiel beim olympischen Gewichtheben, wo aufgrund der Lage der Hantel im Laufe der Kniebeuge, entweder in einer „Frontsquat-Position“, oder gar mit ausgestreckten Armen über dem Kopf, keine sonderliche Lastverschiebung auf die Hüftstrecker stattfinden kann, weil die damit einhergehende Vorwärtsneigung des Oberkörpers darin resultieren würde, dass die Hantel nicht mehr gehalten werden könnte.

Damit einhergehend, wenn die Last für die Kniestrecker sehr anspruchsvoll ist, kann es teilweise auch dazu kommen, dass nicht direkt entgegen der Schwerkraft gearbeitet, sondern vielmehr versucht wird, die Last nach vorne wegzudrücken. Eine Last nicht senkrecht nach oben anzuheben, sondern auf einer schiefen Bahn zu bewegen erscheint einfacher, jedoch führt es dazu, dass die Kniebeuge instabil wird. Die Stabilität wird schließlich nur dadurch aufrechterhalten, dass die Schwerelinie in den Bereich der von den Füßen gebildeten Unterstützungsfläche fällt. Deswegen sollte der Schwerpunkt auch über die ganze Bewegung in etwa oberhalb des Mittelfußes liegen. Der Versuch nicht direkt entgegen der Last, sondern nach vorne weg gegen diese anzudrücken, birgt demnach auch die Gefahr des nach vorne Fallens, wodurch womöglich ein Schritt nach vorne gemacht werden muss, um dies zu verhindern. Im Gewichtheben zum Beispiel gilt das wohlgemerkt aber nicht als Regelverstoß und ist dementsprechend auch durchaus häufiger anzutreffen.

Entlastung von Quadrizeps und Gluteus?! Hamstrings

Die Agonisten der Kniebeuge umfassen zum einen Kniestrecker und zum anderen Hüftstrecker. Seitens der Kniestrecker sind die Quadrizepse die einzigen relevanten Muskeln (neben vorherig besprochenen Aspekten, dass über biartikuläre Muskeln auch andere Muskeln zur Kniestreckung beitragen können). Seitens der Hüftstrecker hingegen gibt es mehrere Beteiligte, wobei der Gluteus unterm Strich aber als der wichtigste anzusehen ist, weil dieser zum einen der stärkste Hüftstrecker ist, über den gesamten Bewegungsradius zur Hüftstreckung beiträgt und anders als zum Beispiel die Hamstrings ein eingelenkiger Muskel ist. Nun kann es bei einer Kniebeuge mit sehr hoher Last oder aber bis zur Ermüdung durchaus dazu kommen, dass sowohl die Quadrizepse als auch der Gluteus an ihre Grenzen kommen. Ein klassischer Fall hierfür wäre eine anfängliche Lastverschiebung auf die Hüfte, um die zu schwachen Quadrizepse zu kompensieren, woraufhin, des höheren Widerstandes wegen, der Gluteus nun aber auch überfordert ist.

In solche einem Fall müssen andere Muskeln Aushilfe bieten. Die Auswahl ist dabei aber recht begrenzt. Eine Möglichkeit ist, dass die Belastung des Gluteus vermehrt auf die Hamstrings verschoben werden kann. Die Hamstrings bilden den Großteil der Muskulatur auf der Rückseite des Oberschenkels und ziehen, wie wir wissen, über die Hüfte als auch über die Knie. Wie weiter oben bereits beschrieben wurde, können sie wegen ihrer meist dominierenden Wirkung der Hüftstreckung (im Vergleich zur Kniebeugung) gemäß dem Lombardschen Paradoxons auch zur Kniestreckung beitragen. Nichtsdestotrotz erzeugen die Hamstrings am Knie trotzdem ein flexions-Drehmoment. Unabhängig davon, ob nun das Netto-Drehmoment zu Gunsten der Knie-Extension ausfällt, reduziert eine übermäßige Lastverschiebung von Gluteus auf die Hamstrings damit die Effizienz, weil der Kniestreckung und damit dem Quadrizeps ein höherer Widerstand gegenübersteht. Bei der Bewegung äußert sich dies nun hierdurch, dass sowohl der Hüft- als auch der Hantelpfad in der konzentrischen Bewegungsphase nach hinten verlaufen, weil die über dominanten Hamstrings zum einen die Hüfte strecken und zum anderen, durch die am Boden fixierten Füße das Knie nach hinten ziehen, sodass der Schwerpunkt Richtung Fersen wandert und eventuell sogar das nach hinten Fallen droht. Dem entgegenzuwirken kann dann eine leichte Dorsalflexion, bzw. Anheben der Zehen folgen.

Entlastung von Quadrizeps und Gluteus?! Adduktor Magnus

Von der sagittalen Betrachtungsebene machen wir einen kleinen Abstich auf die frontale Seite der Bewegung. Auch dort macht sich eine Kompensationsbewegung erkenntlich, die sowohl auf Schwächen im Quadrizeps als auch Gluteus zurückzuführen sein kann und relativ häufig ist. Die Rede ist vom Zusammenführen der Knie in der konzentrischen Bewegungsphase. Um dies zu erkennen, braucht man wohlgemerkt auch gar keine Bewegungsverfolgung, gerade wenn die Kompensation entsprechend stark vertreten ist. Kurz nach Beginn der Konzentrik wandern die Knie also nach medial (X-Bein Haltung), wobei sich diese im oberen Teil der Bewegung dann oftmals wieder aufhebt. In Anbetracht der vorhandenen Muskeln wird dabei auch recht schnell ersichtlich, wessen Muskeln dies zuzuschreiben ist. Nämlich vor allem dem Adduktor Magnus, welcher gerade bei höherer Hüftflexion, also in den unteren Bereichen der Kniebeuge, als potenter Hüftstrecker agiert. Neben seiner Rolle als Hüftstrecker wird er seinem Namen gerecht und adduziert die Beine, was in diesem Fall eben dazu führt, dass die Knie zusammengeführt werden. Normalerweise agiert der Gluteus maximus, als starker Abduktionsmuskel bei gebeugter Hüfte, dem entgegen und hält den Adduktor in einer längeren und stärkeren Position, was schon darauf schließen lässt, dass dieser dem Ganzen nicht ganz gewachsen ist. Wohlgemerkt nimmt der muskuläre Hebelarm des Gluteus maximus mit zunehmender Hüftflexion auch ab, was das Auftreten jener Bewegung dort noch weiter begünstigt. Hand in Hand mit dem Zusammenführen der Knie kann ebenso eine Lastverschiebung auf die Hüfte stattfinden, sodass der dominante Adduktor mehr Last übernehmen kann.

Aber das ist nicht alles. Betrachtet man die Bewegung von frontal, dann wird in unseren Beispielbildern ebenso ersichtlich, dass die dort erkennbaren Hebelarme auf die Knie, durch die Zusammenführung der Knie verringert werden, sodass die Zusammenführung der Knie ebenso als Bewegung zur Entlastung der Kniestrecker dienen kann. Dies wird vor allem relevant, wenn ein breiter Stand gewählt wird, bzw. die Knie sich weiter nach außen und weniger nur gerade nach vorne bewegen.

Entlastung von Quadrizeps und Gluteus?! Pendel

Kommen wir nun zu einer Kompensationsstrategie, welche es ermöglicht sowohl Hüft- als auch Kniestrecker in gewissen Teilen der Bewegung zu entlasten.

Am Beginn der konzentrischen Bewegungsphase startet die Bewegung ähnlich wie die weiter oben angeführte klassische Ausweichbewegung zur Entlastung der Kniestrecker, indem die Hüfte nach hinten oben schießt und die Knie an die Schwerelinie angenähert werden. Anders als bei besagten Bewegungen zur alleinigen Entlastung der Quadrizeps können nun aber die Hüftstrecker jene zusätzliche Last auch nicht mehr bewältigen. Was nun passiert, ist eine Entlastung der Hüftstrecker, indem die Hüfte wieder der Schwerelinie angenähert wird. Wohlgemerkt entfernen sich folglich die Knie wieder von der Schwerelinie, weil sich diese nun aber bereits in einer gestreckteren Position befinden, können sie dieser erhöhten Last besser standhalten. Folglich gerät die Hüfte in eine mechanisch bevorteilte Position und die Bewegung kann beendet werden. Auf diese Weise werden Quadrizeps und Hüftstrecker in unterschiedlichen Abschnitten der Bewegung auf Kosten des jeweils anderen entlastet.

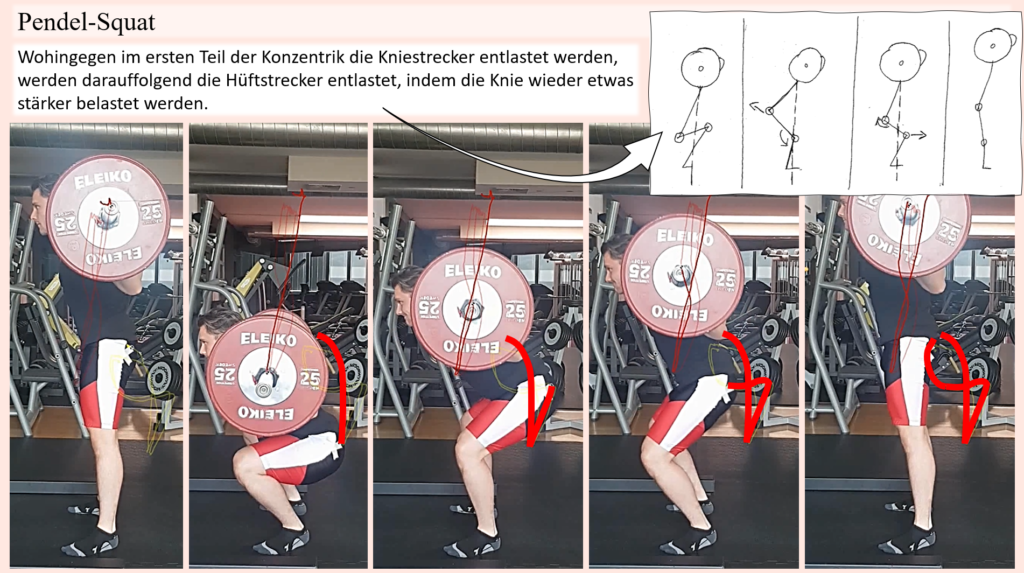
Rundrücken

Auch wenn die Hüft- und Kniegelenke sozusagen den Zentren einer Kniebeugebewegung entsprechen, sind es nicht die einzigen dabei involvierten Strukturen. Gerade wenn die Bewegung mit einer schweren Hantel als Zusatzlast ausgeführt wird, liegt diese in der Regel im Bereich des Nackens bzw. des oberen Rückens, was bedeutet, dass die Last über den Rumpf erst auf das Becken und Beine weitergeleitet wird. Der Rücken bzw. die Wirbelsäule fungiert demnach als Lastableiter, die, um diese Funktion gut zu erledigen, möglichst stabil gehalten werden muss. Dennoch ist die Wirbelsäule überaus beweglich, wobei die Rückenstrecker- bzw. Rumpfmuskulatur mitunter dafür zuständig sind, sie in einer gegebenen Position zu halten und zu stabilisieren. Nun kann es im Laufe einer Kniebeugebewegung aber dazu kommen, dass diese Stabilität teilweise verloren geht, bzw. die Wirbelsäule ein rundet, sei es im Lendenwirbelbereich, wie im anschließenden Absatz besprochen wird, oder auch in der gesamten, bzw. vor allem der Brustwirbelsäule. Das Einrunden der Wirbelsäule kann dabei mehrere Gründe haben. Zum einen besteh die Möglichkeit, dass die Beweglichkeit nicht ausreicht, um eine bestimmte Tiefe zu erreichen, dabei den Schwerpunkt oberhalb des Mittelfußes zu halten, um nicht umzufallen, und gleichzeitig einen geraden Rücken beizubehalten. Die Rundung findet hier, wie weiter unten aufgezeigt, oftmals im Lendenwirbelbereich statt, ist aber nicht zwangsweise darauf beschränkt. Eine andere Möglichkeit wäre, dass die Rückenstrecker, welche der Flexion entgegenwirken, an ihre Grenzen kommen. Unterscheiden zwischen etwaigen Beweglichkeitsschwierigkeiten oder aber muskulären Schwächen kann man dadurch, dass im Falle des Ersteren, das Einrunden bereits in der exzentrischen Bewegungsphase kontinuierlich eintritt, wohingegen bei zu starken Anforderungen für die Rückenstrecker dies vor allem im Laufe der Konzentrik auftritt und ebenso verstärkt wird, wenn die Hantelablage höher ausfällt, weil dann mehr Last auf der Brustwirbelsäule liegt. In diesem Falle können die Anforderungen auf die Rückenstrecker noch weiter erhöht und damit das Einrunden verstärkt werden, wenn eine Entlastung des Quadrizeps stattfindet. Denn hierdurch neigt sich der Oberkörper weiter nach vorne, was vor allem bei einer hohen Hantelablage die Last auf die Brustwirbelsäule weiter erhöht.

Butt-Wink

Als „Butt-Wink“ bezeichnet man umgangssprachlich ein Einrunden der Lendenwirbelsäule im untersten Bereich der Kniebeuge. Auch in diesem Fall wird das fehlende Bewegungsausmaß seitens der Sprunggelenke und der Hüftgelenke durch eine Flexion der Wirbelsäule kompensiert. Verstärkt wird der Effekt dabei zusätzlich, wenn die Bewegung am Beginn der Exzentrik mit einer überstreckten Lendenwirbelsäule (Hohlkreuz) gestartet wird, denn dadurch werden die Hüftgelenke bereits zu Beginn leicht gebeugt und erreichen dann im Laufe der Exzentrik früher ihren Anschlag, woraufhin das Hohlkreuz wieder aufgehoben und womöglich sogar eine Flexion stattfinden muss.

Der Butt-Wink selbst kann dadurch auftreten, dass zum Beispiel die Sprunggelenke nicht beweglich genug sind, um die Knie weit genug nach vorne zu schieben, oder auch das Bewegungsausmaß der Hüftgelenke nicht ausreicht. Was die Hüftgelenke angeht, wird das jeweilige Bewegungsausmaß mitunter von der Form der Gelenkpfanne bzw. des Oberschenkelkopfes und Halses vorgeschrieben, weswegen unterschiedliche Personen eine tiefe Kniebeuge auch mit unterschiedlicher Standbreite besser erreichen können.

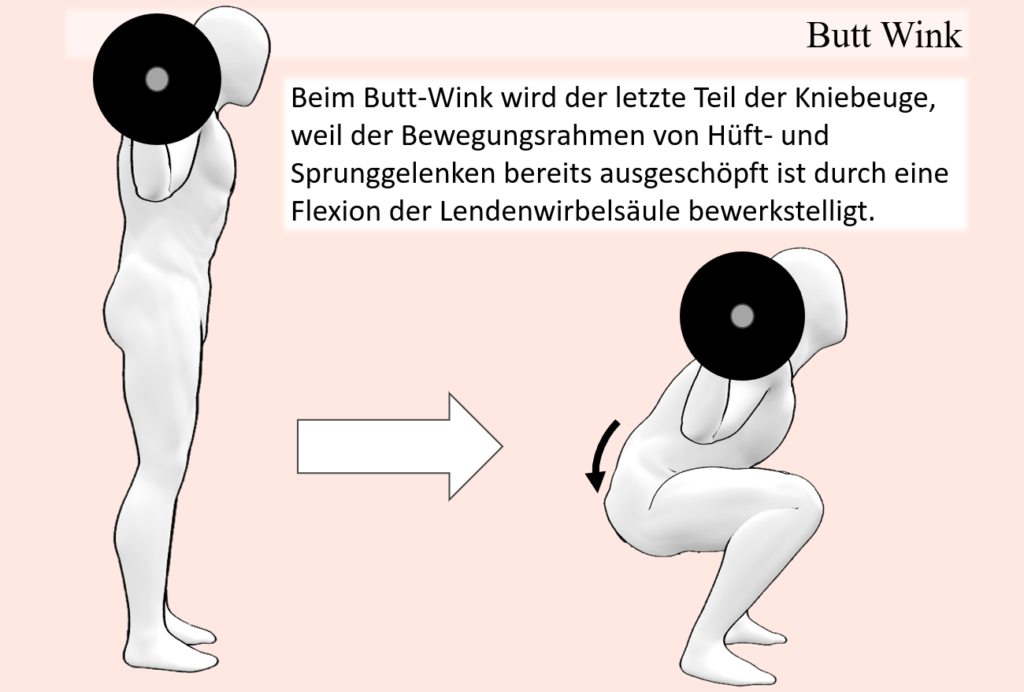
Kreuzheben, Bewegung und zuständige Muskeln

Dadurch dass sich die Kniebeuge und das Kreuzheben stark ähneln, was die belasteten Gelenke und deren Bewegung angeht, sind auch die beteiligten Muskeln sehr ähnlich. Wie auch in der Kniebeuge findet seitens der Knie und Hüfte in der konzentrischen Bewegungsphase eine Extension statt und im Gegenzug bei der Exzentrik eine Flexion. Vor allem, wenn dabei ein breiter Stand gewählt wird („Sumo-Kreuzheben“), dann nimmt seitens der Hüftgelenke, ebenso wie auch bei der Kniebeuge, bei der Konzentrik die Adduktion und bei der Exzentrik die Abduktion zu. Nun gilt hier aber natürlich dasselbe wie auch schon bei der Kniebeuge angesprochen wurde, nämlich, dass in der exzentrischen Bewegungsphase die Knie- und die Hüfte nicht von den Hüft- bzw. Knieflexoren gebeugt werden müssen. Vielmehr sind das die Gelenkbewegungen, welche die Gewichtslast des Körpers und der Hantel verursachen, sodass die jeweiligen Strecker-Muskeln (+ bei breitem Stand Adduktoren) dem entgegenwirken müssen, um die Bewegung zu kontrollieren. Auch hier belaufen sich die beteiligten Muskeln (Agonisten) also vor allem auf Hüft- und Kniestrecker, sowie Adduktoren. Die jeweilige Funktion, welche jene Muskeln nun im Laufe der Bewegung erfüllen, bleibt natürlich auch ähnlich bzw. gleich wie bei den Kniebeugen, schließlich geht dies ja vor allem auf den anatomischen Verlauf der jeweiligen Muskeln zurück. Trotzdem variiert die letztendliche Bewegung durchaus von den Kniebeugen, was daraus resultiert, dass jene Muskeln etwas anders zusammenarbeiten, sprich an unterschiedlichen Punkten der Bewegung mehr oder weniger beteiligt sind. Darauf kommen wir aber gleich, im Kontext der wichtigsten Faktoren für eine mechanisch optimale Kreuzhebe-Bewegung, zurück.

Was die Kniestreckung anbelangt, ist natürlich auch wieder der Quadrizeps der zuständige Muskel, wobei wiederum der Rectus femoris am Knie zwar streckt, in der Hüfte jedoch beugt, was beim Kreuzheben genauso kontraproduktiv sein kann wie bei der Kniebeuge. Ähnliches gilt natürlich für die Hamstrings, welche die Hüfte strecken, aber die Knie beugen. Den Vorteil, den jene beiden Muskeln mit sich bringen, indem sie es nämlich ermöglichen, Kräfte zwischen Knie- und Hüfte zu übertragen, haben wir bereits angesprochen. Hierzu wird auf das weiter oben beschriebene lombardsche Paradoxon verwiesen. Was nun die Hüftstreckung betrifft, erinnert auch das stark an die Kniebeuge. Der Gluteus (Maximus) ist der stärkste und wichtigste Strecker im Hüftgelenk und kann hierbei von den Hamstrings und dem Adduktor Magnus unterstützt werden, wobei letzterer besonders bei stärkerer Flexion und breiterem Stand vermehrt mit ins Spiel kommt. Neben einer zunehmenden Adduktion/Abduktion bei zunehmend breitem Stand, tendiert Kreuzheben mit breitem Stand auch dazu, gerade am Beginn der Konzentrik im Vergleich zu einem schmalen Stand Quadrizepslastiger zu sein, was ersichtlich wird, wenn man die Startposition samt beispielhafter Hebelarme auf die Gelenke von frontal betrachtet.

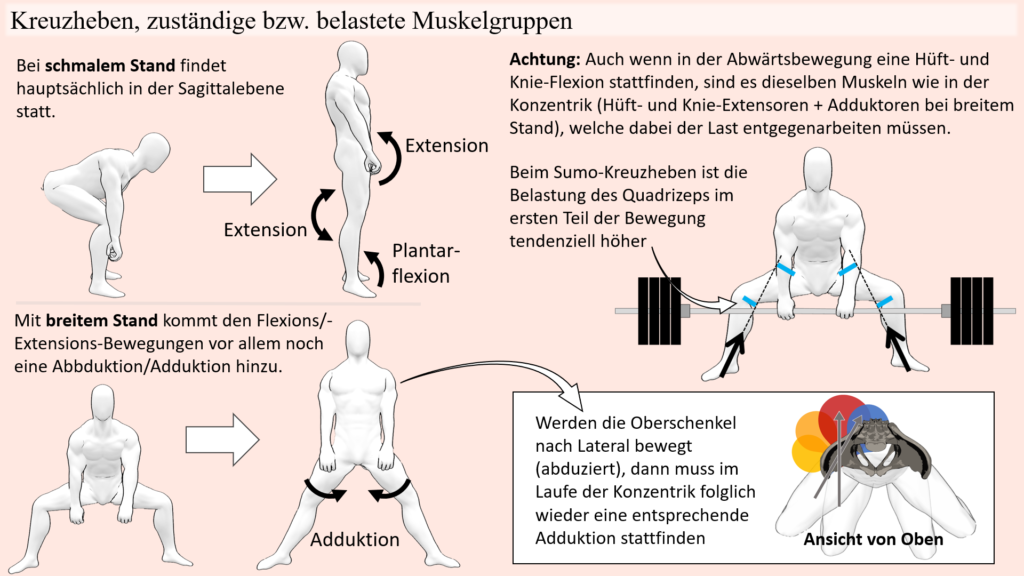
Kompensationsstrategien beim Kreuzheben

Kommen wir nun auch im Falle des Kreuzhebens zu einigen Kompensationsbewegungen, die auftreten, um gewisse Schwachpunkte zu kompensieren. Das Prinzip der Lastverschiebung mittels Annäherung und Entfernung der Gelenke an die Schwerelinie bleibt dabei wie gehabt, weswegen wir auch hier auf einigen Parallelen zu entsprechenden Kompensationsstrategien bei der Kniebeuge stoßen werden. Aber auch gewisse Unterschiede werden ersichtlich, was sich bereits in den folgenden Aspekten einer mechanisch optimalen Bewegungsausführung zeigt.

Wichtige Aspekte für das mechanisch optimale Kreuzheben

Der wesentliche Punkt, worin sich Kniebeugen und Kreuzheben (ausgeführt mit einer Langhantel) unterscheiden, ist, dass im Falle des Kreuzhebens die Stange vor dem Körper, entlang der Beine geführt wird, bzw. werden muss. Dies hat nämlich zur Folge, dass, mit Ausnahme einiger Fälle des Sumo-Kreuzhebens, die Knieflexion limitiert wird, weil die Hantel im Laufe der Bewegung nun mal an den Knien vorbei muss, woraus folgt, dass sich diese, sobald es dazu kommt, hinter der Stange befinden müssen.

Sumo-Kreuzheben kann hier unter Umständen eine Ausnahme bilden, weil bei sehr breitem Stand, wobei die Füße fast parallel zur Stange liegen, fast ausschließlich eine Abduktion/Adduktion der Oberschenkel stattfindet. Das heißt, es findet kaum eine Bewegung vor- und zurück innerhalb der Sagittal-Ebene statt, weswegen sich das mit den Knien über der Stange quasi erübrigt. In solch einem recht seltenen Fall kann dann sogar eine simultane Hüft- und Kniebewegung stattfinden. Wenn es hingegen um Kreuzheben mit schmalem Stand, bzw. Sumo-Kreuzheben mit etwas schmaleren Stand geht, dann muss die Bewegung zweiphasig erfolgen. Wohingegen sich in der Kniebeuge Hüft- und Kniegelenke simultan bewegen, wenn keine sonderliche Lastverschiebung stattfindet, so teilt sich die Kreuzhebe-Bewegung in zwei Phasen. Zunächst strecken sich die Knie, wobei der Oberkörper im selben Winkel nach oben bewegt wird (zeigt sich dadurch, dass Hüft- und Schulterpfad die gleiche Strecke zurücklegen), bis die Hantel die Knie passiert hat, woraufhin eine Hüftstreckung stattfindet.

Bis auf diesen Unterschied sind die anderen Faktoren für eine mechanisch optimale Bewegung jenen der Kniebeuge sehr ähnlich. So wird auch beim Kreuzheben die Unterstützungsfläche von den Füßen gebildet, woraus folgt, dass der Schwerpunkt, welcher sich aus Hantel und Körper ergibt, innerhalb dieser Fläche, optimalerweise über dem Mittelfuß gehalten werden muss, um nicht nach vorne oder hinten umzufallen. Was hierfür beim Kreuzheben noch hinzukommt, ist die Lage der Schultern, welche sich möglichst senkrecht oberhalb der Stange befinden sollten/müssen. Ist dies nicht der Fall, dann droht die Gefahr, sobald die Hantel angehoben wird, dass die Arme der Schwerkraft wegen nach vorne in ihre senkrechte Ausrichtung schwingen, was eventuell sogar zum Umfallen nach vorne führt. Durch Kontraktion des Latissimus wird zwar die Hantel an den Körper gezogen, bzw. gehalten, jedoch ist dies bei einer schweren Hantel und zu weit vorne gelegenen Schultern natürlich nur noch schwer bis gar nicht möglich.

Was den Rücken angeht, fungiert dieser auch hier als Last-Ableiter, das bedeutet, die Wirbelsäule sollte in einer starren Position stabilisiert werden, sodass Kräfte effizient weitergeleitet und nicht durch Wirbelsäulenbewegungen verpuffen.

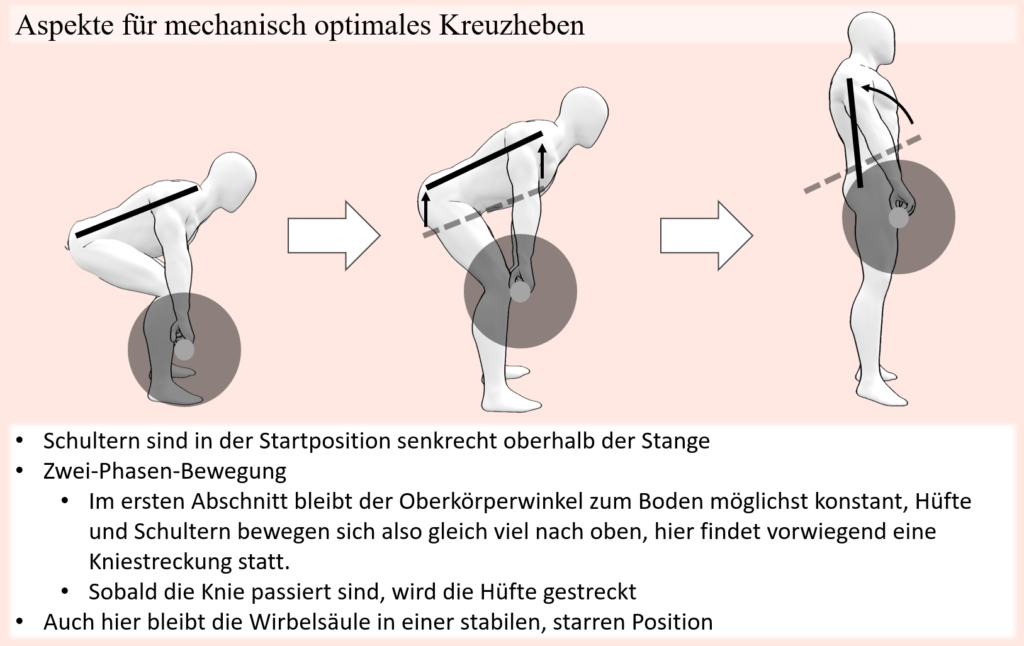
Entlastung der Quadrizeps

Auch im Falle des Kreuzhebens drehen sich sehr viele Kompensationsstrategien um zu schwache Knie- und oder Hüftstrecker, wobei es seitens der Knie um die Quadrizepse und seitens der Hüfte vor allem um den Gluteus geht (beim Sumo Kreuzheben mit sehr breitem Stand werden die Adduktoren ebenso sehr wichtig).

Kann der Quadrizeps seinen Anforderungen, welche darin bestehen, den ersten Teil der Bewegung zu leiten und dadurch Schulter und Hüfte im gleichen Maße nach oben zu bewegen, nicht gerecht werden, dann muss dieser sich Hilfe seitens der Hüftstrecker suchen. Folglich werden die Knie zurück, näher an die Schwerlinie gezogen, im gleichen Zuge wird die Hüfte nach oben bewegt und der Oberkörper neigt sich etwas weiter nach vorne. Die Abweichung zum oben besprochenen Optimum, wo Quadrizeps und Hüftstrecker ihren jeweiligen Beitrag geben, zeigt sich folglich in der ungleichen Aufwärtsbewegung der Hüfte und der Schulter. Wohingegen die Hantel sowie die Schulter erst einen geringen Weg hinter sich haben, hat sich die Hüfte bereits nach oben bewegt, um die Knie zu entlasten. Ebenso werden die Hamstrings durch die Kniestreckung gedehnt und können damit mehr Kraft zur Hüftstreckung beitragen. In gestreckterer Position liegt nun weniger Last auf den Knien, jetzt muss die Bewegung aber fast ausschließlich von den Hüftstreckern getragen werden.

Entlastung von Quadrizeps und Gluteus?! Hamstrings

Im Falle der Kniebeuge haben wir bereits eine Kompensationsstrategie angetroffen, bei welcher nicht der Gluteus Maximus der dominierende Hüftstrecker ist, sondern dessen mangelnde Kraft von den Hamstrings kompensiert wird. Bei der Bewegung selbst zeigte sich dies durch den Bewegungspfad der Hantel, der Hüfte und auch des Schwerpunktes, welche im Laufe der Konzentrik nach hinten verliefen. Hier, im Kontext des Kreuzhebens, kommt etwas sehr Ähnliches, bzw. im Prinzip gleiches zum Vorschein, wenn sich die Hamstrings als dominant herausstellen. Auch hier wandert die Hüfte sowie auch die Hantel auf ihrem Weg nach oben nicht auf einer geraden Bahn, sondern vielmehr auf einer Kurvenbahn nach hinten. Folglich wird auch der Schwerpunkt eher auf die Fersen verlagert. Die Hamstrings, die zwar die Hüftstreckung unterstützen und so den Gluteus, welcher diese nicht im ausreichenden Maße bewältigen kann, aber auch hier ziehen sie entgegen der Kniestreckung und erhöhen damit den Widerstand für die Quadrizepse.

Entlastung von Quadrizeps und Gluteus?! Hitching

Analog zur oben besprochenen Kompensationsstrategie bei der Kniebeuge, wo Hüftstrecker und Kniestrecker in unterschiedlichen Abschnitten der Bewegung auf Kosten des jeweils anderen entlastet werden, kann auch beim Kreuzheben eine ähnliche Situation entstehen, so wie in der Grafik unten auch zu erkennen ist. Wie auch bei der Kniebeuge beginnt die Bewegung klassischerweise damit, dass die Knie entlastet werden, weil sie der anfänglichen Belastung nicht gerecht werden können. Das heißt wie auch bei der oben beschriebenen Kompensationsbewegung zur Entlastung der Kniestrecker wird die Last auf die Hüftstrecker verschoben, die Hüfte bewegt sich nach oben, die Knie strecken sich und der Oberkörper neigt sich weiter nach vorne. Die Knie werden entlastet und die Hamstrings unterstützen vermehrt die Hüftstreckung. Der folgende Abschnitt der Bewegung wird nun aus dieser Position heraus absolviert, jedoch kommen auch diese an ihre Grenzen. Sobald aber die Hantel die Knie passiert hat, gibt es einen Ausweg, nämlich indem die Knie wieder etwas gebeugt werden. Anders als bei der Kniebeuge ist hier nämlich die Stange vor dem Körper, sodass die Knie nicht gebeugt werden können, wenn die Stange sich noch an den Schienbeinen befindet. Ist sie aber erstmals oberhalb der Knie, können diese unter der Stange nach vorne geschoben werden, wodurch sich der Hebelarm auf die Hüftgelenke wieder verringert. Auch hier ist dies besonders ersichtlich am Hüftpfad, welcher kurzzeitig sogar wieder nach unten verläuft, ebenso wie dem Hantelpfad, welcher mitsamt den Oberschenkeln auch etwas nach vorne bewegt wird. Aus dieser Position heraus, wo die Hantel zum Teil fast schon am Oberschenkel aufliegt, werden dann Knie und Hüfte letztlich vollständig gestreckt.

Entlastung von Quadrizeps und Gluteus?! Adduktor Magnus

Der Adduktor Magnus ist neben den Hamstrings ein entscheidender Unterstützer des Gluteus bei der Hüftstreckung, vor allem bei starker Hüftbeugung. Gerade im Falle des Sumo-Kreuzhebens (sowie Sumo-Kniebeugen) steigt seine Relevanz aber nochmals an, weil bei entsprechender Bewegung mit einem breiteren Stand auch vermehrt eine Adduktion stattfinden muss. Ebenso wird der Adduktor Magnus durch abduzierte, also abgespreizte Beine in eine längere Position gebracht und kann damit mehr Kraft erzeugen, die zur Hüftstreckung, aber eben auch zu Adduktion beitragen kann. Wie bereits im Kontext der Kniebeugen angesprochen fungiert der Gluteus dabei als Gegenspieler, welcher verhindert, dass der Adduktor Magnus die Oberschenkel nach innen zieht, wodurch er ihn gleichermaßen in einer längeren und damit stärkeren Position hält. Wenn nun aber der Gluteus dieser Aufgabe nicht gewachsten ist, sondern der Adduktor dominiert, ist das Resultat etwas ganz Ähnliches, wie wir bereits bei der Kniebeuge gesehen haben, indem die Beine kurz nach Beginn der Konzentrik mehr oder weniger stark zusammengeführt werden.

Auch hier kann durch jenes Zusammenführen der Beine ebenso der Quadrizeps etwas entlastet werden, weil die Gelenke der Wirkungskraftlinie angenähert werden, was aus frontaler Perspektive ersichtlich wird.

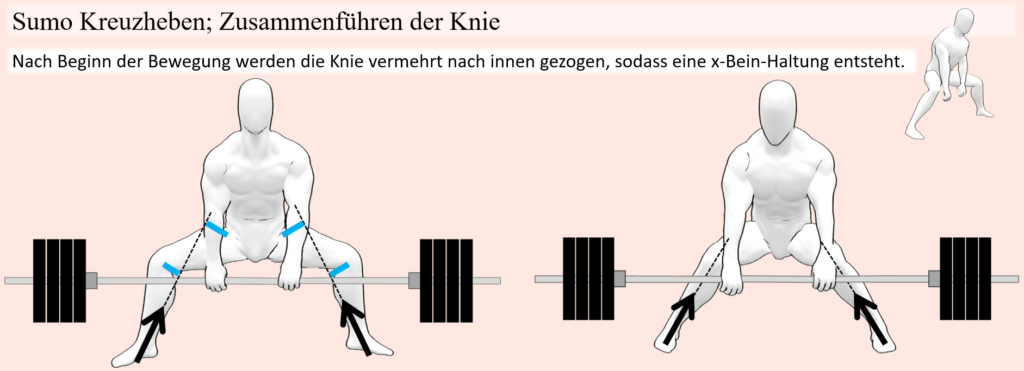
Rundrücken

Weil die Hantelstange beim Kreuzheben nicht auf dem Rücken aufliegt und somit auch nicht zum Beispiel durch eine „lowbar-Ablage“ die Belastung der Brustwirbelsäule verringert werden kann, sondern die Last der Hantelstange an den Armen angreift und der Rücken als Lastleiter dient, kommt es gerade beim Bewegen von schweren Lasten häufig zu einer Einrundung des Rückens. Dies kann dabei im Grunde die gesamte, unter Last stehende Wirbelsäule betreffen, sei es die Lenden oder auch die Brustwirbelsäule. Warum genau es aber zum Einrunden kommt, kann verschiedene Ursachen haben. Wie auch bereits bei der Kniebeuge angesprochen kann eine Möglichkeit sein, dass die Beweglichkeit nicht ausreicht, um in die notwendige Position zu kommen. Anders als bei der Kniebeuge, wo es einer gewissen Beweglichkeit vor allem seitens der Hüft- und Sprunggelenke bedarf, um mit physiologisch geradem Rücken in eine tiefe Hocke zu kommen, fallen beim Kreuzheben die Sprunggelenke hierbei weg, schließlich können die Knie der Hantel wegen gar nicht sonderlich weit nach vorne bewegt werden. Dementsprechend kommt es vor allem auf die Flexionsfähigkeit der Hüfte an. Reicht diese nicht aus, um mit den Händen an die Stange zu kommen, dann muss die fehlende Strecke vom Rücken kompensiert werden. Falls dies aber wirklich der Fall sein sollte, dann wird dies bereits in der Startposition ersichtlich und nicht etwa erst unter einer hohen Last. Kann die Starposition hingegen problemlos eingenommen werden und erst zu Beginn oder im Laufe der Bewegung rundet der Rücken ein, dann hat dies Last bezogene Ursachen. Doch auch hier gibt es mehrere Möglichkeiten. Eine naheliegende Vermutung könnte natürlich sein, dass die Rückenstrecker ihren Anforderungen nicht gerecht werden und dadurch die Flexion nicht verhindern können, sei es im Bereich der Lenden,- oder auch der Brustwirbelsäule. Und obwohl dies natürlich durchaus möglich ist, kann das Problem auch ganz woanders, nämlich bei den eigentlichen Agonisten der Bewegung, nämlich den Hüft- und Kniestreckern liegen. Egal ob eine Einrundung im Lendenwirbel- oder im Brustwirbel-Bereich auftritt, reduziert dies im Vergleich zu einem physiologisch geraden Rücken nämlich die Hebelarme auf die Hüftgelenke, weil diese durch den Rundrücken näher an der Schwerlinie bleiben. In diesem Sinne kann es zu solch einer Kompensation also kommen, wenn die Hüftstrecker ihren Anforderungen nicht gerecht werden, vielleicht auch in Kombination mit zu schwachen Kniestreckern, welche im Vorhinein vermehrt Last auf die Hüfte geschoben haben. Ebenso kann durch eine Flexion der Wirbelsäule der nötige Flexionswinkel der Hüftgelenke in einer gegebenen Position verringert werden. Das wiederum versetzt vor allem den Gluteus in eine mechanisch bessere Lage, weil dessen muskulärer Hebelarm bei stärkerer Flexion abnimmt.

Schwachpunkt Latissimus

Zu guter Letzt kommen wir neben all den Punkten zu den Agonisten der Bewegung zu einem Hilfsmuskel beim Kreuzheben, nämlich dem Latissimus. Dieser ist im Laufe der Bewegung neben seiner stabilisierenden Funktion des Rückens und seiner unterstützenden Rolle für die Hüftstreckung dafür zuständig, die Hantelstange an den Beinen zu halten. Ein wesentlicher Aspekt hierfür wurde bereits weiter oben bei den Aspekten des mechanisch optimalen Kreuzhebens angeführt, nämlich dass die Schultern sich stets oberhalb der Hantelstange befinden, um ein Ausschwingen der Schwerkraft wegen zu verhindern.

Würde die Lage der Hantel aber ausschließlich der Lage der Schultern und der Schwerkraft überlassen werden, welche die Arme wie zwei Seile senkrecht zum Boden ausrichtet, dann könnte eine kleine Last- bzw. Schwerpunktverschiebung auf den Vorderfuß bereits ausreichen und die Hantelstange droht nach vorne zu schwingen. Auch bei anderen Kompensationen, in denen der Oberkörper durch eine Lastverschiebung nach vorne kippt, sodass sich die Schultern leicht vor der Hantelstange befinden, droht, ohne entsprechende Beteiligung des Latissimus, das nach vorne Fallen. Und selbst wenn dies verhindert werden kann, so vergrößert sich dennoch der Hebelarm auf die Hüftgelenke. Damit fällt dem Latissimus also durchaus eine äußerst wichtige Rolle zu.

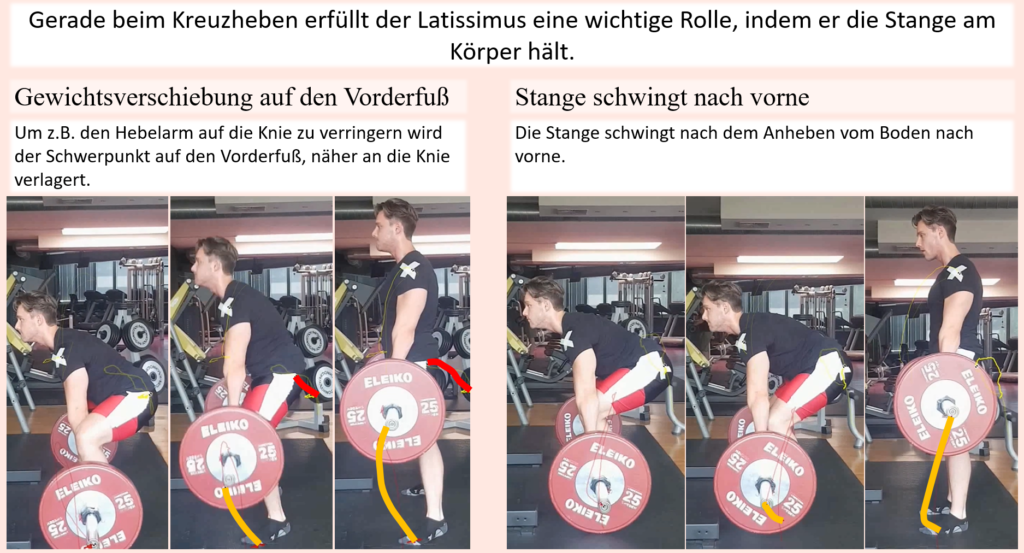
Bankdrücken, Bewegung und beteiligte Muskeln

Die dritte und letzte Bewegung, welche wir uns im vorliegenden Abschnitt ansehen, ist das allseits bekannte Langhantelbankdrücken. Wohingegen es bei den Kniebeugen sowie dem Kreuzheben hinsichtlich Agonisten vor allem um die untere Extremität ging, umfasst das Bankdrücken vielmehr die obere Extremität, wobei die eigentliche Bewegung bereits im Namen grob ersichtlich wird, schließlich liegt man mit dem Rücken auf einer Bank und drückt eine Hantel von sich weg. Um die zuständigen Muskeln zu definieren, ist solch eine vage Beschreibung aber eher weniger gut geeignet. Brechen wir die Bewegung also etwas genauer herunter. Die Körperachse selbst befindet sich in einer parallel zum Boden verlaufenden Position, wobei die Arme senkrecht nach oben ausgestreckt sind und mit den Händen eine Hantel gehalten wird, welche beide Hände miteinander verbindet. Im Folgenden wird jene Hantel abgelassen, also in Richtung Boden und so in Richtung Körper bewegt. Die Gelenke, welche hierfür nötig sind, sind vor allem Schulter- als auch Ellbogengelenke. Dadurch dass letzteres nur eine Bewegungsachse aufweist, ist es einfach zu schlussfolgern, dass im Ellbogen, welcher bei senkrecht nach oben ausgestreckten Armen gestreckt ist, eine Flexion stattfinden muss, um die Hantel abzulassen (bzw. eine Extension, um die Hantel folglich wieder hochzudrücken). Was die Schulter angeht, ist es schon etwas komplexer, schließlich weist diese mehrere Freiheitsgrade auf. Betrachtet aus der Transversalebene könnte man nun meinen, dass zum Ablassen lediglich eine „horizontale Abduktion“ und zum Hochdrücken dementsprechend eine „horizontale Adduktion“ im Schultergelenk stattfindet. Hierbei würde sich die Hantel aber auf einer senkrechten Bahn vom Ausgangspunkt oberhalb der Schultern nach unten bewegen und schließlich im Bereich der Schlüsselbeine den Körper berühren. In aller Regel ist dies aber nicht die Bewegung, welche tatsächlich stattfindet, oder zumindest wäre es meist eine mechanisch recht ineffiziente und auch unpraktikable Bewegungsausführung. Was man vielmehr beobachten kann, ist, dass die Hantel meistens irgendwo vom mittleren bis unteren Brustbein mit dem Körper in Berührung kommt und ihre tiefst gelegene Stelle erreicht. Auf diesen Punkt, bzw. welchen Vorteil dies verschafft, kommen wir gleich zurück, wenn es um wichtige Aspekte für mechanisch vorteilhaftes Bankdrücken geht, aber für die Schulterbewegung bedeutet dies, dass nicht nur eine horizontale Abduktion/Adduktion stattfindet, sondern die Hantel aus sagittal betrachtet auch einen horizontalen Weg zurücklegt, wobei in der Schulter eine Extension/Flexions-Bewegung erfolgt.

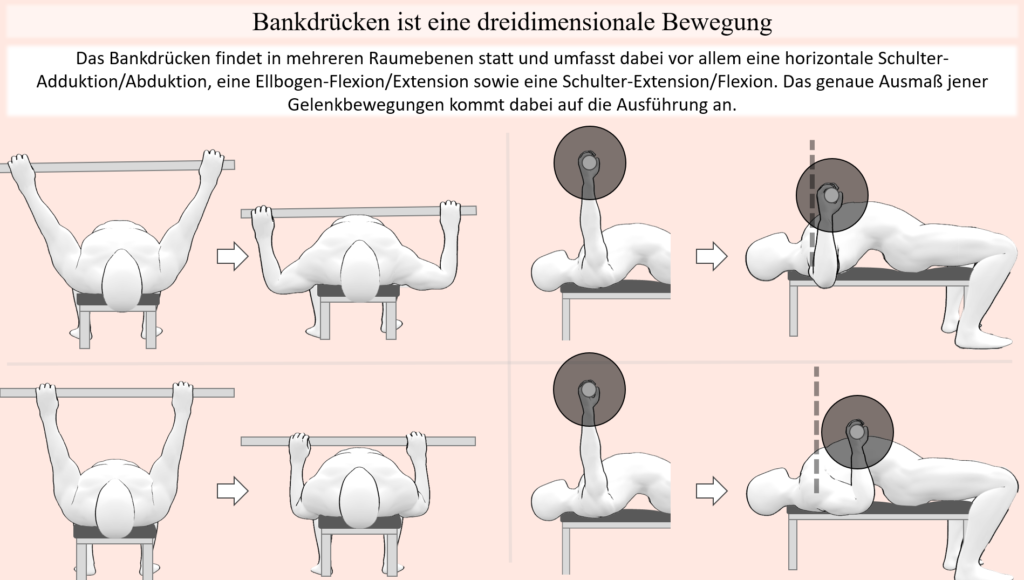
Wie immer gilt es nun auch hier die wirkende Last miteinzubeziehen, wobei klar wird, dass die Gewichtskraft, der nach unten wirkenden Hantel, die Abwärtsbewegung leitet, indem im Laufe der Exzentrik im Ellbogen ein „Flexions-Drehmoment“, sowie in der Schulter aus transversal betrachtet ein „Abduktions-Drehmoment“ und aus sagittal betrachtet ein „Extensions-Drehmoment“ erzeugt wird. Dasselbe gilt für die Konzentrik, wobei seitens der Ellbogen/ Ellbogenstrecker-Muskeln und seitens der Schulter Muskeln, welche für die horizontale Adduktion und Flexion verantwortlich sind, dafür zuständig sind, jenen Widerstand durch ein entgegengesetztes Drehmoment zu überwinden. Dabei ist der wichtigste Ellbogenstrecker natürlich der Trizeps, wohingegen für die horizontale Adduktion und Flexion der Schulter vor allem der große Brustmuskel, Pectoralis major, sowie der vordere Teil des Delta-Muskels zuständig sind. Und auch in der Exzentrik sind es vor allem jene Muskeln, welche die Abwärtsbewegung der Hantel abbremsen müssen und nicht etwa Ellbogenbeuger, welche jene Bewegung leiten. Damit hätten wir die wichtigsten Agonisten der Bewegung. Deren jeweilige Beteiligung variiert nun je nach Bewegungsabschnitt, bzw. Übungsausführung. Wird beispielsweise ein engerer Griff gewählt, dann liegt der Hantelablagepunkt weiter Fußwärts, wodurch zum einen, aus der Sagittalperspektive betrachtet, der horizontale Weg ansteigt und zum einen auch der „Extensions-Hebelarm“ auf das Schultergelenk, schließlich ansteigt, je weiter sich die Hantel horizontal von der Schulter entfernt, was ebenso bedeutet, dass jene Hebelarme im Laufe der Konzentrik abnehmen, schließlich befindet sich die Hantel in der Endposition direkt oberhalb der Schultergelenke. Folglich muss auch die Kraft der Muskulatur, welche dem entgegensteht, in jenen Positionen ansteigen, wo der Widerstand vermehrt zu einer Schulter-Extension führt, was vorwiegend den vorderen Delta-Muskel aber auch den Pectoralis major betrifft.

Ähnliches gilt in der Transversalansicht, wobei das abspreizend wirkende Drehmoment der Last ansteigt, wenn die Hantel abgelassen wird, sodass Muskeln, welche die horizontale Adduktion erzeugen (vor allem Pectoralis major) entsprechend stärker beansprucht werden. Ebenso kann entsprechender Abduktions-Hebelarm auf die Schulter bei einem breiteren Griff länger ausfallen als bei einem schmalen Griff, wobei wohlgemerkt die Reibungskraft an der Hantel beachtet werden muss, weswegen die Griffweite hier keinen so großen Unterschied macht, wie man vielleicht denken mag (vor allem, wenn es um einen „breiten Griff“ und einen „etwas breiteren Griff“ geht). Dennoch, würde die Bewegung mit schulterbreitem Griff ausgeführt werden, dann bestünde diese seitens der Schultern hauptsächlich aus einer Schulter-Extension/Flexion.

Der Ellbogen wiederum streckt bzw. beugt sich über die ganze Bewegung, wobei die Beteiligung des Trizepses klassischerweise im oberen Bereich der Bewegung als relevanter eingeschätzt wird. Ein Grund hierfür könnte sein, dass je nach Griffbreite im unteren Bereich des Bankdrückens eine zu starke Trizepskontraktion dazu führen könnte, dass die Stange in Richtung Bauch bewegt wird, wenn sich die Ellbogen strecken. Ebenso, wenn man die einzelnen Köpfe des Trizeps etwas genauer betrachtet, wird man feststellen, dass nur zwei der drei Köpfe eingelenkig sind. Der lange Trizepskopf entspringt nämlich am Schulterblatt und zieht demnach neben dem Ellbogen auch über das Schultergelenk. Neben seiner Funktion als Ellbogenstrecker unterstützt er demnach in den meisten Positionen noch dazu die Schulter-Extension. Nun ist dies aber gegensätzlich zur Schulter-Flexion, die im Zuge des Bankdrückens, vor allem im unteren Bereich, von anderen Muskeln bewerkstelligt werden muss. Durch seine Schulter-streckende Funktion zieht der lange Kopf des Trizeps den Oberarm einfach gesagt nach unten, sodass der Widerstand für die Schulter-Flexion zusätzlich zur wirkenden Last erhöht wird. Unterm Strich ist es aber gerade beim Bankdrücken mit eher breitem Griff schwierig einzelnen Muskeln exakte Aufgaben beziehungsweise Bereiche der Bewegung zuschreiben, weil die einzelnen Muskeln sich in ihren jeweiligen Bewegungsfunktionen unterstützen können. Dies gilt vor allem, wenn die Bewegung vermehrt einer geschlossenen kinematischen Kette entspricht.

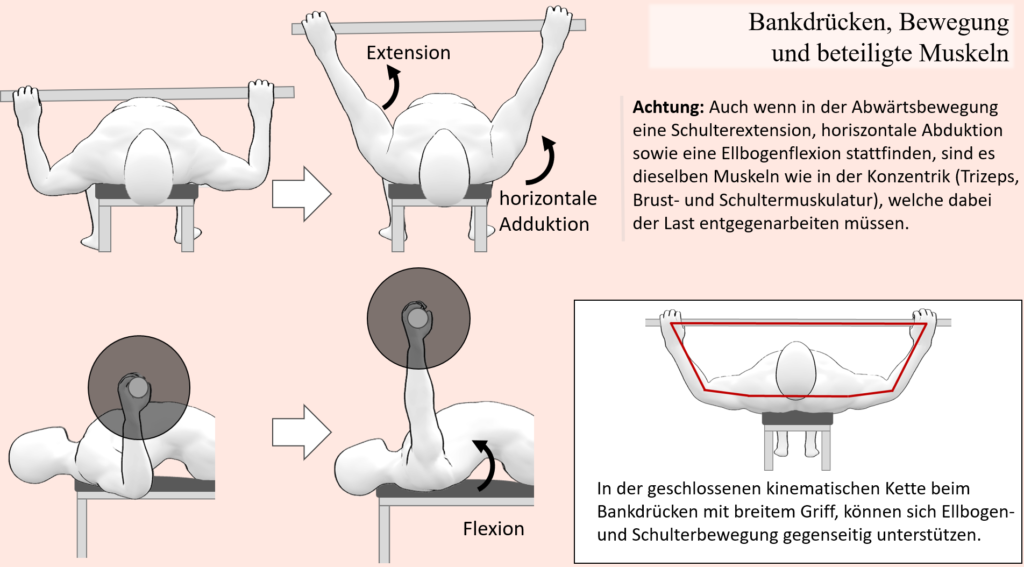
Wichtige Aspekte für das mechanisch optimale Bankdrücken

Wenn die Rede von „mechanisch optimalem Bankdrücken“ ist, dann geht es vielmehr darum, sich die Frage zu stellen, durch welche Aspekte, bzw. wie die Bewegung ausgeführt werden solle, damit der Bewegungsapparat beim Bankdrücken aus mechanischer Sicht möglichst vorteilhaft ist.

Anders als bei den oben angesprochenen Kniebeugen und Kreuzheben, bei denen das Gleichgewicht ein fundamentaler Aspekt ist, sodass jeweiligen Bewegungen, samt eventueller Lastverschiebungen, gezwungenermaßen im Rahmen eines relativ konzentrierten Schwerpunktes ablaufen müssen, ist dies beim Bankdrücken nicht der Fall. Hier liegt man auf einer Bank und läuft nicht Gefahr, umzufallen. Aus diesem Grund ist hinsichtlich dessen der Bewegungspfad auch nicht so eingeschränkt, sondern könnte freier gewählt werden. Was hier nun aber einen gewissen Rahmen vorgibt ist die zu leistende Arbeit, was vor allem darauf abzielt, eine wie weite Strecke die Hantel bewegt werden muss. Würde die Hantel ausgehend von der liegenden Position mit senkrecht nach oben ausgestreckten Armen lediglich auf einer senkrechten Bahn nach unten und wieder hoch bewegt werden, dann könnte man zunächst vielleicht glauben, dass hierdurch oben erwähnte Schulter-Extension/Flexion wegfallen würde. Ebenso ist die kürzeste Strecke zwischen zwei Punkten eine Gerade. Doch mit Ausnahme einiger Extreme würde sich der Hantelablagepunkt am Körper hierdurch im Bereich der Schlüsselbeine oder gar des Halses befinden, was den zurückzulegenden Weg deutlich erhöht. Vielmehr sollte man anstreben, die Hantel am höchsten Punkt des Körpers abzulegen, um die Strecke zu verringern.

Was den Bewegungspfad angeht, auf welchem die Hantel von der obersten zur untersten Position und wieder zurückbewegt wird, gibt es auch hier einen wesentlichen Unterschied, gerade zu den oben beschriebenen Kniebeugen. Dort nämlich ist man daran versucht, den konzentrischen Bewegungspfad dem exzentrischen anzugleichen, weil dies bedeutet, dass keine Muskeln zu schwach sind und durch Ausweichbewegungen kompensiert werden müssen. Beim Bankdrücken hingegen unterscheidet sich die Abwärtsbewegung ganz entscheidend von der Aufwärtsbewegung, und das gewollt. Wie an einem anderen Punkt bereits angeschnitten entspricht das Bankdrücken unter gewissen Voraussetzungen nämlich einer geschlossenen kinematischen Kette. Das gilt dann, wenn die Stange sich oberhalb der Schultergelenke und in einer Linie mit den Ellbogen befindet. Sich an jene Position anzunähern verschaff deswegen Vorteile, weil Schulter- und Trizeps-Bewegungen sich gegenseitig unterstützen. Wohingegen in der exzentrischen Bewegungsphase die Stange also auf einer schiefen Bahn vom obersten Punkt hin zum höchsten Punkt des Körpers (Ablagepunkt) bewegt wird, wird die Hantel in der darauffolgenden Konzentrik schneller wieder in Richtung geschlossene kinematische Kette zurückbewegt. Unterstützt wird dies optimalerweise, indem der Ablagepunkt möglichst erhöht und den Schultern angenähert wird, was zum einen durch eine sogenannte Brücke (Hohlkreuz) sowie nach unten (Fußwärts) gezogenen Schulterblättern erreicht wird. Hierdurch wird nicht nur der senkrechte, sondern auch der horizontale Weg und folglich vor allem auch die in der Sagittal-Ebene zu sehenden Hebel auf die Schultergelenke verringert, sondern eventuell kann ein größerer Anteil der Bewegung in einer eher geschlossenen kinematischen Kette absolviert werden und noch dazu kann man sich das dritte Newtonsche Gesetz zunutze machen.

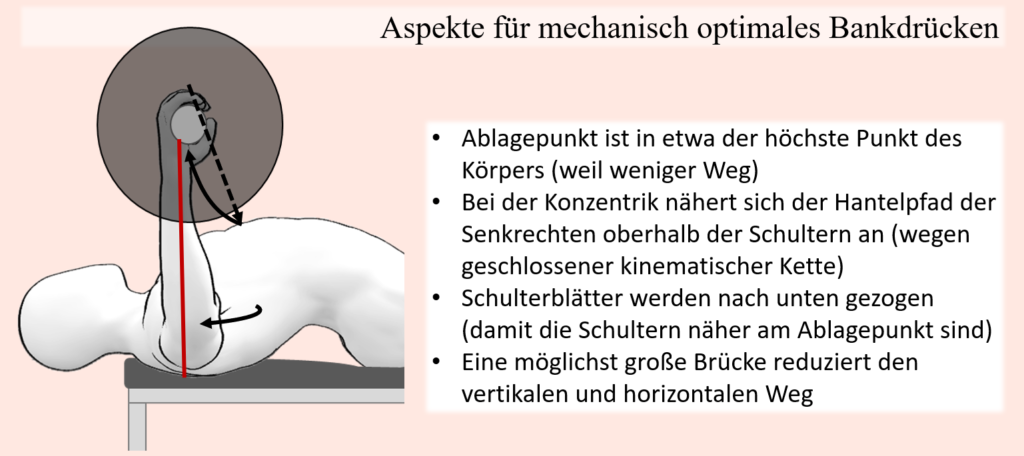
Kompensationsstrategien im Bankdrücken

Kommen wir nun auch im Falle des Bankdrückens zu Kompensationsbewegungen. Anders als bei den vorherig besprochenen beiden Übungen stellt sich dies hier aber teilweise etwas verschieden dar. Bei den Kniebeugen/Kreuzheben konnten wir Kompensationsbewegungen anhand von Bewegungsabweichungen festmachen und ausgehend davon dann auf muskuläre Schwächen schließen. Dies erfordert aber, dass die Bewegung, also im oberen Falle die Kniebeuge oder das Kreuzheben, durch unterschiedliche Koordination der einzelnen Gelenke absolviert werden, bzw. die Last vermehrt von bestimmten Muskeln übernommen werden kann, was sich in besagten Kompensationsstrategien zeigt. Beim Bankdrücken ist dies aber nur bedingt der Fall. Wie wir in einigen unteren Beispielen sehen werden, können zwar Kompensationsbewegungen entstehen, bei welchen über andere Muskeln oder auch durch Geschwindigkeit und passive Kräfte versucht wird, den Agonisten des Bankdrückens unter die Arme zu greifen, jedoch können diese nicht etwa wie in der Kniebeuge entlastet werden, indem beispielsweise fast die ganze Last von den Knien auf die Hüfte verlagert wird. So kann die Bewegungsausführung und damit die in den Gelenken stattfindende Bewegung durch Dinge wie die Griffbreite, die Stärke des Hohlkreuzes und den Ablagepunkt beeinflusst werden, im Laufe einer Bewegung aber kann nicht einfach der Brustmuskel großartig entlastet werden. In der geschlossenen Bewegungskette können sich die Muskeln zwar gegenseitig aushelfen, jedoch bedeutet dies auch, dass deren etwaige unterschiedliche Beteiligung der geschlossenen Kette wegen nicht so einfach durch die äußere Betrachtung festgemacht werden kann. Aus diesen Gründen wird beim Bankdrücken, neben dem Hantelpfad, von welchem Abweichungen vom mechanischen Optimum ersichtlich werden können, vor allem auch von der Stelle des jeweiligen Sticking Points bzw. der Stelle, wo das Bewegungsversagen bei hoher Last oder Ermüdung eintritt, auf eventuelle Schwächen geschlossen. Sehen wir uns hierzu also ein paar Beispiele an.

Intuitive Ausweichbewegung in die geschlossene kinematische Kette

Vergleicht man den Bewegungspfad beim Bankdrücken erfahrener und weniger erfahrener Athleten, dann wird man oftmals feststellen, dass bei ersteren der Bewegungspfad im Wesentlichen dem oben geschilderten mechanischen Optimum entspricht, also die Hantel in der Konzentrik schnell wieder zurück, über die Schultern gebracht wird. Bei Anfängern, wie wir weiter unten in einer Darstellung auch nochmals sehen werden, tendiert der Hantelpfad hingegen oftmals deutlich geradliniger zu sein, sodass die Exzentrik einer Verbindungslinie vom obersten Punkt zum Ablagepunkt entspricht, in der darauffolgenden Konzentrik die Hantel aber fast senkrecht vom Ablagepunkt nach oben gedrückt wird. Wie gesagt, auf ein Beispiel hierzu kommen wir weiter unten nochmal zurück. Um was es an diesen Punkt vielmehr gehen soll, ist eine intuitive Ausweichbewegung in eine mechanisch günstigere Position, welche in solch einem Falle vereinzelt, auftreten kann. Und zwar geht es dabei um ein plötzliches Zurückziehen der Ellbogen, was man durchaus ab und zu, selbst bei Trainingsanfängern beobachten kann, wenn die Last besonders hoch, oder die Bewegung bis zur Ermüdung ausgeführt wird. Das ist gewissermaßen der Versuch des Körpers, die zu schwachen Muskeln für die mechanisch unvorteilhaftere Position zu kompensieren, indem eine hoffentlich bessere Position eingenommen wird.

Aushilfe durch den Serratus

Die beim Bankdrücken notwendige horizontale Adduktionsbewegung wird vom Trizeps, der vorderen Schulter und natürlich vor allem dem Brustmuskel erzeugt. Sind jene Muskeln nicht stark genug, um denWiderstand zu überwinden, oder kommen zumindest nahe an ihre Grenzen, dann kann die Last nicht von anderen Muskeln übernommen werden. Hierdurch kann es aber zu einer Kompensationsbewegung kommen, bei welcher versucht wird, die Schulterblätter aktiv nach vorne zu schieben und dadurch die Hantel weiter nach oben zu drücken. Der hierfür zuständige Muskel ist der Serratus anterior, welcher seitlich am Brustkorb sitzt, auf der Innenfläche des Schulterblattes ansetzt und es bei seiner Kontraktion nach vorne (bzw. in diesem Fall nach oben in Richtung Decke) zieht. Bei der Bewegung kann sich dies dadurch zeigen, dass die Schulterblätter übermäßig bewegt werden oder gar die Schultern im Laufe der Konzentrik leicht angehoben werden, wohingegen sich die Schulterblätter normalerweise zwar bewegen, aber eben nur so weit als nötig, um die Schultergelenkbewegung zu ermöglichen. Wohlgemerkt ist diese Kompensationsbewegung eher eine Verzweiflungstat und vermag es nicht wirklich signifikant Last von den Agonisten zu nehmen und diese damit zu entlasten. Vielmehr liegt die Hoffnung darin, dadurch die Hantel womöglich durch die Sticking Region zu bringen.

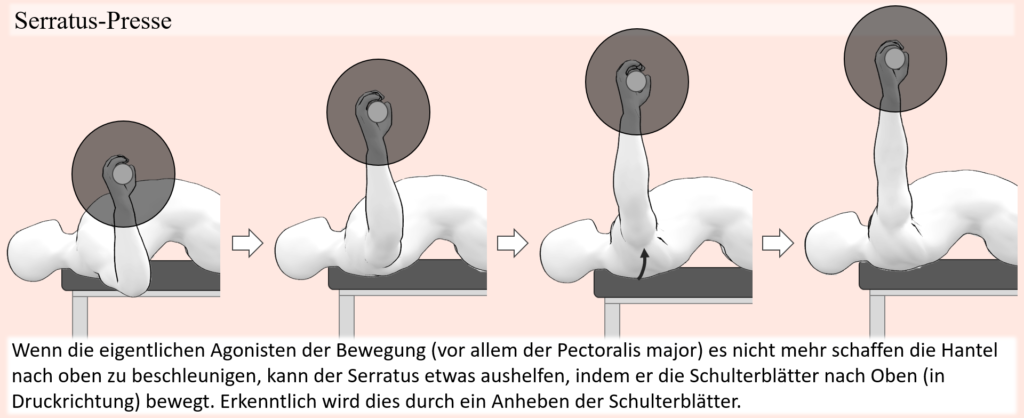
Hintern hoch

Wenn Bankdrücken mit hohen Lasten oder bis zur Ermüdung ausgeführt wird, ist wohl eine der am häufigsten zu beobachtenden Folgebewegungen, wenn die reine Krafterzeugung der Agonisten nicht mehr ganz ausreicht, das Anheben des Gesäßes, durch die Kraft, welche über die Beine auf den Boden ausgeübt wird. Die Gründe, warum es überhaupt dazu kommt, können zum einen eine technische Komponente haben, sodass die Übungsausführung fast schon prädestiniert dafür ist, dass sich das Gesäß von der Bank abhebt, auch wenn die Muskeln die Last vielleicht sogar bewältigen könnten, oder auch eine muskuläre Komponente, wo es den Muskeln tatsächlich nicht mehr möglich ist, ausreichend Kraft auf die Stange zu bringen, um diese weiterhin nach oben zu beschleunigen. Im letzteren Falle kann das Abheben des Gesäßes zwei Vorteile mit sich bringen. Zuallererst ist die auf den Boden ausgeübte Kraft ein wesentlicher Teil des „Setups“, also der Positionierung, bevor die eigentliche Bewegung überhaupt initiiert wird. Diese Kraft dient nämlich dazu, den Oberkörper auf der Bank nach hinten zu drücken, sodass die Schulterpartie der Reibung wegen (die Bank sollte also nicht rutschig sein) in ihrer nach unten gezogenen Position gehalten werden, als auch die Brücke (das Hohlkreuz) aufrechterhalten, bzw. maximiert werden kann. Um dies zu erreichen, sollte entsprechende Kraft also den Körper auf der Bank in Kopfrichtung drücken und nicht dazu genutzt werden, um das Gesäß anzuheben. Das ist im Wesentlichen das, was vorhin mit Problemen in der Bewegungsausführung gemeint war. Dadurch, dass die Beine also die Brücke halten bzw. erzeugen, kann über der Stange auch ein Impuls mitgegeben werden. Dies betrifft sowohl den im nächsten Beispiel aufgegriffenen Fall, wo das Einsinken der Stange am Ablagepunkt als passive Kraft genutzt wird, um sie folglich wieder nach oben zu beschleunigen, als auch, wenn der Hintern von der Bank abhebt. Passiert dies nämlich simultan mit dem Versuch, die Stange vom Ablagepunkt hochzudrücken, kann durch das Anheben des Körpers, die Stange schlichtweg etwas angeschoben werden. An einem höheren Punkt der Bewegung kann durch das Anheben des Gesäßes die Hantel, falls dies nicht schon der Fall ist, in die geschlossene Bewegungskette gebracht und noch dazu der untere Teil der Brustmuskulatur besser involviert werden. So oder so, insofern die Übungsausführung dies nicht prädestiniert, ist das Anheben des Gesäßmuskels schlichtweg eine Notlösung, um die zu schwachen Agonisten zu kompensieren und die Hantel über die Sticking Region zu bringen.

Einsinken im Brustkorb

Weniger eine Kompensationsbewegung, sondern vielmehr ein Technikaspekt, welcher oftmals genutzt wird, um höhere Lasten zu bewegen, sind passive Kräfte. Besteht die Möglichkeit durch bestimmte Interventionen passive Kräfte, welche den aktiven Kräften zuarbeiten, zu erhöhen, kann dies aus biomechanischer Sicht natürlich Vorteile mit sich bringen. Neben passiven Kräften, welche durch die bloße Dehnung der beteiligten Muskel-Sehnen-Einheiten entstehen, geht es beim Bankdrücken hierbei vor allem um den Kontakt der Stange mit dem Brustkorb. Sinkt die Stange hierbei in den Brustkorb ein, dann wirkt der Stange dabei natürlich ein Widerstand entgegen, den es zu überwinden gilt, damit die Stange überhaupt einsinken kann. Diese Kräfte entlasten damit gleichermaßen die Muskulatur, bzw. unterstützen die Aufwärtsbeschleunigung, wenn die Stange den Brustkorb wieder verlässt. Ebenso wird durch solch ein Einsinken in den Brustkorb der Zeitraum verlängert, indem die Stange beschleunigt werden kann, bevor sie den Brustkorb verlässt. Der Impuls, welcher der Stange hierdurch mitgegeben wird, kann wiederum dann unter Umständen genutzt werden, um den Sticking Point zu überwinden, der sich beim Bankdrücken oftmals einige Zentimeter oberhalb der Brust befindet.

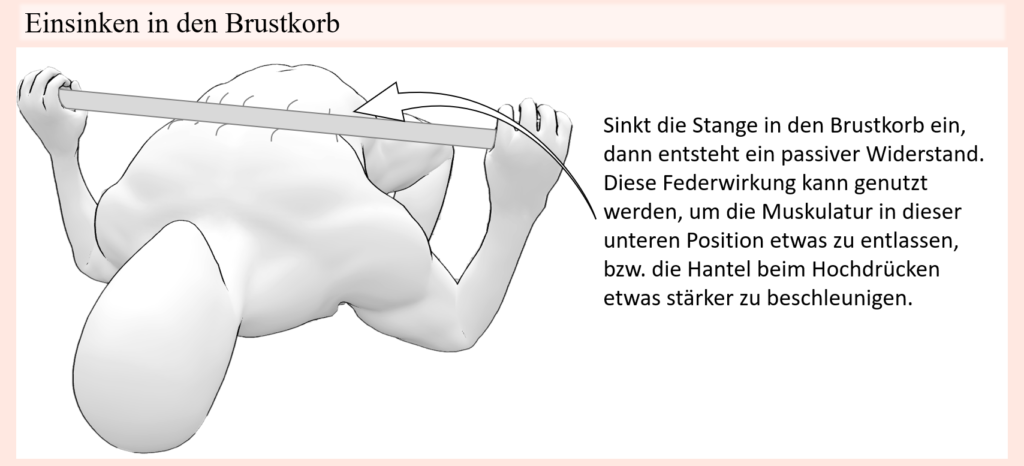
Suboptimaler Hantelpfad

Kommen wir nun zu guter Letzt noch auf einen Faktor zu sprechen, welcher weniger mit einer Kompensationsbewegung zu tun hat, aber die Ursache sein kann, warum eine Kompensation auftritt, bzw. eine jeweilige Last nicht überwunden werden kann. In Bezug des Kreuzhebens und der Kniebeugen ist der Bewegungspfad, insofern keine Kompensationsbewegung stattfindet und der Schwerpunkt über dem Mittelfuß gehalten wird, mehr oder weniger vorgeschrieben. Beim Bankdrücken kann dieser stärker variieren, was andererseits bedeuten kann, dass es in diesem Falle vielleicht eine größere Rolle spielt, eine mechanisch vorteilhaftere Ausführung anzutrainieren und nicht nur die Agonisten zu stärken, wenn das Ziel ist, hohe Lasten zu bewegen. Das beste Beispiel hierfür ist die weiter oben angesprochene Beobachtung, dass gerade Trainingsanfänger oftmals einen mechanisch unvorteilhafteren Bewegungspfad einschlagen. In den angeführten Videoframes ist dies deutlich zu erkennen. Der Trainierende bewegt die Hantel in Richtung Ablagepunkt, drückt diese aber fast senkrecht von dort nach oben. Aus mechanischer Sicht macht er sich hiermit die Bewegung schwieriger als nötig. Würde die Hantel im Laufe der Konzentrik zügiger in Richtung Schultern gebracht werden, könnte von den entsprechenden Vorteilen profitiert werden.

Bei vielen anderen Trainingsmaschinen bleibt der Betrag der Kraft, die auf den Trainierenden einwirkt, konstant, wie auch in einigen den obigen Beispielen ersichtlich wurde. Worauf schon an anderen Stellen ausdrücklich hingewiesen wurde, bedeutet dies aber keineswegs, dass der Widerstand für die Bewegung auch gleichermaßen konstant wäre, weil sich die Hebelarme auf beteiligte Gelenke trotzdem verändern können. Aus diesem Grund bieten freie Gewichte oder auch simple Kabelzüge, bei denen der Betrag einwirkender Kräfte konstant bleibt, bei den meisten Bewegungen keineswegs einen konstanten Widerstand. Dies ist wohl der häufigste Fehlglaube, wenn es um Widerstandsprofile und Kraftkurven geht. Ein weiterer ist, dass Kraft- und Widerstandsprofile unveränderlich sind, sprich eine bestimmte Bewegung hat eine jeweilige Kraftkurve und einer Hantel oder einer Trainingsmaschine ist ein ganz bestimmtes Widerstandsprofil zuzuweisen. In Realität ist dies aber nicht wirklich so, weil sie drastisch von Aspekten wie Geschwindigkeit und Beschleunigung beeinflusst werden. Wenn beispielsweise eine 100 kg Langhantel angehoben wird, geht man im Allgemeinen davon aus, dass die auf den Körper einwirkende Kraft 100 kg beträgt und dass diese Langhantel über den gesamten Bewegungsbereich einen Widerstand von 100 kg ausübt. Wenn sich die 100 kg Langhantel jedoch bewegt, kann der Widerstand, den sie bietet, von mehr als 100 kg bis zu weniger als 100 kg variieren, abhängig von der Beschleunigung der Bewegung. Das Gleiche gilt auch für Trainingsmaschinen. Gewissermaßen wird dies von Trainierenden auch oftmals unbewusst oder auch bewusst ausgenutzt, indem in einem Teil der Bewegung eine stärkere Beschleunigung stattfindet, umfolglich einen anderen, anspruchsvolleren Teil der Bewegung besser oder überhaupt überbrücken zu können. Das heißt nicht nur Positions- und Bewegungsänderung sowie Konstruktionselemente wie Kurvenscheiben und Hebel vermögen es Widerstandsprofile zu verändern. Und was Kraftkurven angeht, sind auch diese keineswegs Konstanten, sondern neben Aspekten wie Hebel, welche auf die Gelenke einwirken, und Längenpositionen der jeweiligen Muskeln beeinflusst, auch die Kontraktionsform und Geschwindigkeit, als auch muskuläre Ermüdung jeweilige Kraftkurven. So kann ein Trainierender bei einer regulären Bankdrück-Bewegung in der Regel im oberen Bereich der Bewegung, wo die Arme zunehmend gestreckter sind, mehr Gewicht bewegen, sodass der anspruchsvollste Abschnitt sich im unteren Teil befindet. Führt der Trainierende nun aber viele Wiederholungen aus und nähert sich dem Muskelversagen an, dann stellt man klassischerweise fest, dass die Hantel über den unteren Teil der Bewegung zwar bewegt werden kann, es jedoch am Lockout scheitert. Diese Unbestimmtheit, wenn es um Kraft- und Widerstandsprofile geht, zieht sich aber noch weiter, wenn es um die Frage geht, ob es überhaupt sinnvoll bzw. notwendig ist, Widerstandsprofile an Kraftkurven anzupassen. Diese Frage wird hier nicht genauer beleuchtet, weil es dabei vielmehr darum geht, ob abgestimmte Kraft- und Widerstandsprofile Vorteile hinsichtlich des Trainingseffektes mit sich bringen oder nicht, was nicht ins Thema des vorliegenden Abschnittes fällt. Trotzdem sei gesagt, dass eine Maschine oder Trainingsübung, deren Widerstandsprofil schlechter an jeweilige Kraftkurven angepasst ist, deswegen nicht zugleich auch minderwertiger wäre.

Fassen wir also einige gängige Missverständnisse bzw. falsche Annahmen rund um Kraft und Widerstandsprofile nochmals kurz zusammen:

Freie Gewichte und Kabel stellen einen konstanten Widerstand dar.
Das „Variations-Profil“ hinsichtlich des Betrages der auf den Trainierenden einwirkenden Kräfte ist gleich das Widerstandsprofil einer Trainingsmaschine.
Das Widerstandsprofil wird nicht durch Beschleunigung beeinflusst.
Eine Trainingsübung hat ein ideales Widerstandsprofil.
Wenn Widerstandsprofil und Kraftkurve nicht übereinstimmen, handelt es sich um eine „schlechte“ Trainingsübung.
Kraftkurven beziehen keinen Widerstand mit ein, sondern beschreiben die Krafterzeugungseigenschaften der Muskeln.
Kraftkurven sind konstant und verändern sich nicht.

Spezielles Trainingsequipment

Die bis zu diesem Punkt aufgezeigten Bauweisen von Trainingsmaschinen decken den absoluten Großteil der gängigen Trainingsmaschinen ab. Das heißt aber nicht, dass es nicht auch andere Bauweisen und Arten von Trainingsmaschinen gibt. Die mechanischen Grundlagen bleiben natürlich generell gültig, worin sich gewisse Trainingsmaschinen bzw. Trainingsequipment jedoch unterscheidet ist die Widerstandsquelle. Die bis zu diesem Punkt besprochenen Maschinen funktionieren über Gewichtsscheiben oder Blöcke deren Gewichtskraft direkt oder über Verbindungsglieder auf den Trainierenden einwirkt. Das heißt, dies sind gewissermaßen alles Maschinen die, wie auch freie Hanteln, auf Gravitationskräften beruhen. Und auch wenn dies die Regel ist, gibt es mittlerweile Trainingsmaschinen, welche etwas anders funktionieren. Darunter sind hydraulische sowie vor allem pneumatische Trainingsmaschinen.

Bei pneumatischen Maschinen wird der Bewegungswiderstand durch Luftdruck erzeugt. Das Funktionsprinzip beläuft sich kurz gesagt auf einen Kompressor, welcher Luft in einen Zylinder pumpt, der mit einem Kolben ausgestattet ist, der die Luft während der konzentrischen Phase weiter komprimiert und von der Luft während der exzentrischen Phase der Bewegung wieder herausgedrückt wird. Da die Luft während der konzentrischen Bewegungsphase weiter komprimiert wird, erhöht sich dabei der Widerstand. Der Trainierende kann den Widerstand aber auch mit Handtasten oder Fußpedalen steuern, die den Widerstand während der Bewegung erhöhen, indem mehr Luft eingepumpt oder verringern, indem Luft herauslassen wird. Denn dadurch, dass der Widerstand auf den Luftdruck basiert, bedeutet ein höherer Luftdruck einen größeren Widerstand und ein geringerer Luftdruck einen geringeren Widerstand. Diese Form des Widerstands könnte durchaus einige Vorteile mit sich bringen. Zum einen unterliegt sie nicht den Beschränkungen der Masse und ihrer Trägheitseigenschaften, wodurch das Widerstandsprofil auch weniger von Beschleunigung beeinflusst wird. Ebenso verzichtet man dadurch auf große und schwere Gewichtswiderstände, spart Zeit, Platz und kann den Widerstand, ohne auf gewisse Gewichtsabstufungen beschränkt zu sein, per Knopfdruck variieren, sogar währenddessen eine Bewegung ausgeführt wird.

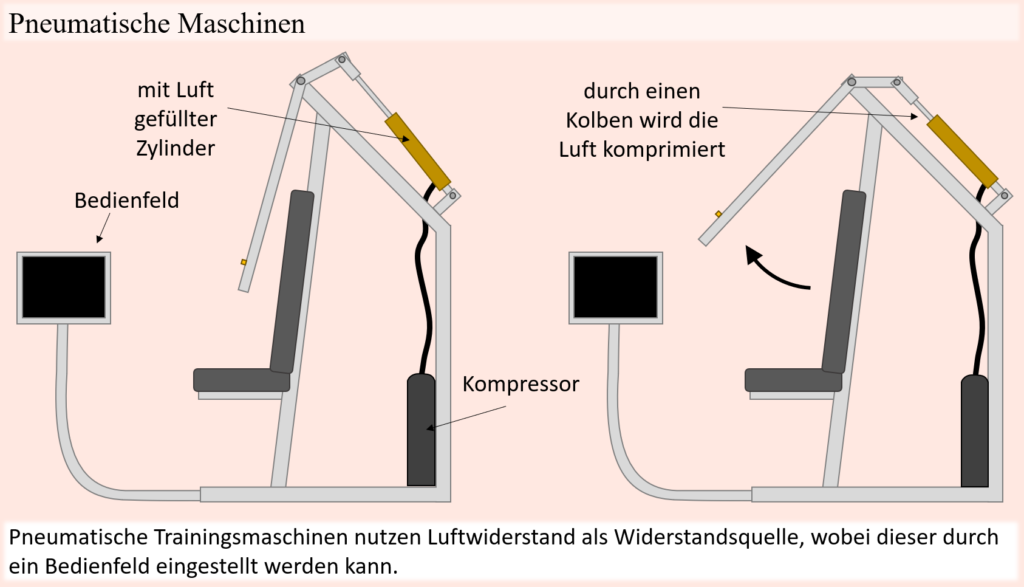
Es gibt viele Trainingsgeräte, die mit dieser pneumatischen Widerstandstechnologie entwickelt wurden, wobei im Grunde jede erdenkliche Trainingsmaschine, welche mit Gewichtswiderständen konstruiert ist, auch auf pneumatischer Basis konstruiert werden könnte. Wenn man sich also pneumatische Trainingsmaschinen ansieht, dann funktionieren sie im Wesentlichen gleich, nur dass der Widerstand eben von einem mit Luft gefüllten Zylinder ausgeht. Und auch wie im Falle Gewichts-basierter Trainingsmaschinen gibt, es hier ebenso die Möglichkeit Kabel und Umlenkrollen zu integrieren, die so eingestellt werden können, dass sie den Widerstand in die gewünschte Richtung umleiten. Ebenso gibt es Power-Racks, die so konzipiert sind, dass sowohl Masse als auch Luftwiderstand integriert werden können, indem an einer Langhantel, welche ganz normal mit Gewichtsscheiben beladen werden kann, zusätzlich Kabel befestigt werden können, sodass neben der Gewichtskraft der Hantel durch pneumatische Elemente auch ein Luftwiderstand miteinbezogen werden kann. Dabei kann Masse und Luftwiderstand im beliebigen Verhältnis kombinieren werden.

Eine andere Form des Widerstands, welche der Pneumatik stark ähnelt, verwendet hingegen eine Flüssigkeit (Öl), um den Widerstand zu erzeugen. Dabei spricht man von hydraulischen Trainingsmaschinen. Bei dieser Form des Widerstands treibt die Bewegung einen Kolben an, der die Flüssigkeit durch eine kleine Öffnung drückt und so den Widerstand erzeugt. Der Unterschied zwischen pneumatischem und hydraulischem Widerstand liegt in der Kompressibilität der Flüssigkeit, die für den Widerstand verwendet wird. Die beim pneumatischen Widerstand verwendete Luft ist komprimierbar und daher werden die Kräfte, die beim Komprimieren während der konzentrischen Phase aufgewendet werden, während der exzentrischen Phase zurückgegeben. Das beim hydraulischen Widerstand verwendete Öl ist im Wesentlichen inkompressibel und daher bietet der hydraulische Widerstand keinen exzentrischen Widerstand während der Bewegung, was natürlich ein Nachteil sein kann.

Eine weitere Kategorie von Trainingsmaschinen sind sogenannte isokinetische Maschinen, wobei man solche meist wohl eher bei Forschungszwecken und weniger im Studio nebenan finden wird. Isokinetische Maschinen ermöglichen es, die Kontraktionsgeschwindigkeit über einen bestimmten Bewegungsradius hinweg konstant zu halten. Bewerkstelligt wird dies, indem im Laufe der Ausführung einer Übung der Muskelanstrengung des Trainierenden ein proportionaler Widerstand entgegengesetzt wird, der die Kontraktionsgeschwindigkeit aufrechterhält. Im Gegensatz zu anderen Krafttrainingsgeräten sind isokinetische Geräte computergesteuert und können so programmiert werden, dass sie über einen bestimmten Bewegungsrahmen funktionieren oder nur konzentrischen oder exzentrischen Widerstand bieten. Aber aufgrund der hohen Kosten und erforderlichen Kenntnissen hinsichtlich Computerprogrammierung werden isokinetische Maschinen normalerweise nur in klinischen, Rehabilitations- und Laborumgebungen eingesetzt. Darüber hinaus handelt es sich hierbei vorwiegend um eher einfache Maschinen, welche eingelenkige bzw. vorwiegend zweidimensionale Bewegungen zulassen (zum Beispiel Bizepscurl oder Leg-Extension).

Einfache Mittel für variablen Trainingswiderstand

Neben speziell konstruierter Trainingsmaschinen gibt es auch ganz simple und äußerst gängige Möglichkeiten vorhandene Trainingswiderstände zu beeinflussen. So werden schon lange elastische Widerstände in Form von unterschiedlich steifen Widerstandsbändern verwendet, um Widerstandsprofile beim Training mit zum Beispiel Langhanteln zu manipulieren. Solche Gummibänder bieten während einer Bewegung unterschiedlich viel Widerstand, da das Gummiband umso mehr Kraft erzeugt, je stärker es gedehnt wird. Je nachdem wie solche Widerstandsbänder nun integriert werden, kann damit dieser elastische Widerstand unterschiedlich eingesetzt werden. Dasselbe gilt natürlich für Trainingsmaschinen, denn auch hier kann, wenn gewollt, mit etwas Fantasie meistens ein elastischer Widerstand zum regulären Widerstand addiert werden.

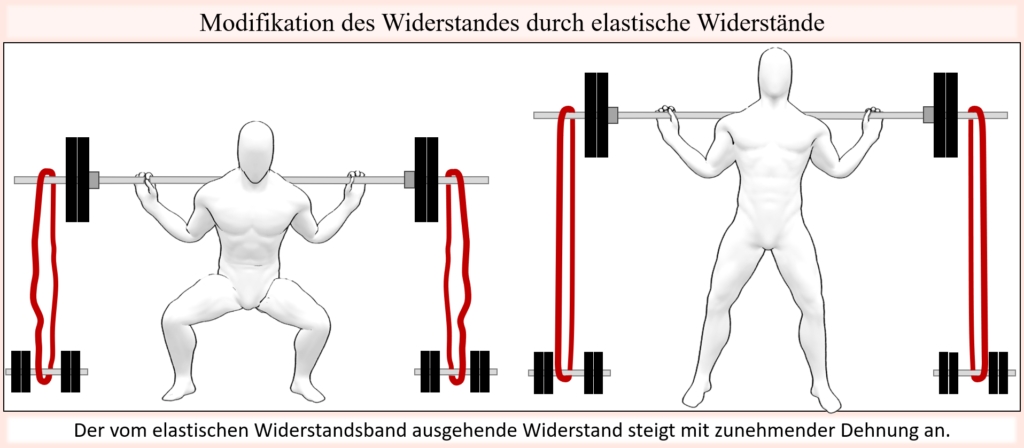
Neben elastischen Widerständen wird auch häufig die Masse der Last in unterschiedlichen Bereichen der Bewegung variiert, um folglich den Widerstand zu variieren, der aus der Gewichtskraft jener Massen entsteht. Bei herkömmlichen Hantelscheiben oder Gewichtsblöcken ist dies nicht besonders praktikabel, jedoch gibt es hierfür simple Lösungen. So werden schon lange, zusätzlich zu jeweiligen Gewichtswiderständen durch Scheiben und Hanteln z.B. lange Ketten verwendet, welche mit einem Ende z.B. an der Langhantel befestigt sind. Wird nun beispielsweise eine Kniebeuge ausgeführt, dann lastet das Gewicht der Hantel und der Gewichtsscheiben über die gesamte Bewegung auf dem Trainierenden. Das Gewicht der Kette liegt aber nur zum Teil auf der Hantel und damit dem Trainierenden, bzw. der relative Anteil variiert je nach Bewegungsposition. Denn je nachdem in welchem Abschnitt der Bewegung sich der Trainierende befindet, liegt ein unterschiedlich großer Anteil der Kette auf dem Boden auf, wodurch in tieferen Beugepositionen die Gesamtlast, die auf den Trainierenden einwirkt, verringert ist.

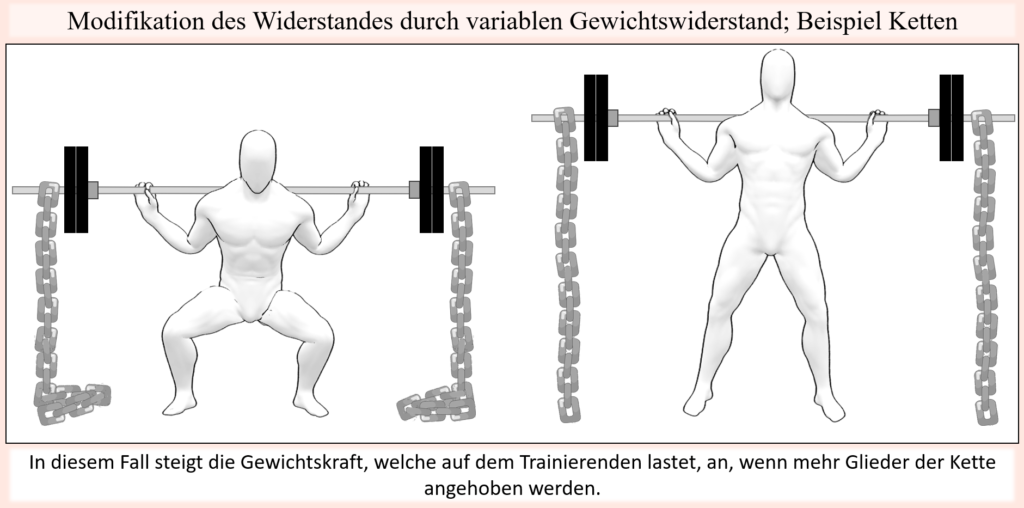
Kinematische Ketten

Wie groß ist der Betrag einer auf den Körper einwirkenden Last? Wo ist deren Kraftangriffspunkt? Wohin verläuft die Kraft und ausgehend davon in welchen Gelenken erzeugt dies wie starke Drehmomente? Das sind Fragen, welche man sich im Kontext der biomechanischen Wirkung einer Trainingslast stellen muss. Im Allgemeinen kann man hieraus dann auch die muskuläre Belastung abschätzen, also folgern welche Muskeln überhaupt bei entsprechender Bewegung beteiligt sind und grob auch in welchem Ausmaß diese Muskeln aktiv sind, als Schlussfolgerung darauf, wie viel Kraft sie denn erzeugen müssen. Dies funktioniert besser bei simplen eingelenkigen Bewegungen, weil hierbei die Wirkung einer einwirkenden Kraft in Bezug auf dieses eine Gelenk und hierfür zuständige Muskeln einfacher nachzuvollziehen ist. Bei komplexeren Bewegungen wird dies schon etwas schwerer, aber auch hier, wenn man solch eine Bewegung herunterbricht und sich ansieht, wie sich die einzelnen Gelenke bewegen und wie die einwirkenden Kräfte diese Gelenke belasten, dann kann man auch hier einigermaßen gut die muskuläre Belastung und Beteiligung schlussfolgern. Dies funktioniert aber nur, wenn sich die jeweiligen Gelenke unabhängig voneinander bewegen. Und damit kommen wir in den Bereich der kinematischen Ketten. Hier geht es um ein aus dem Ingenieurswesen entlehntes Konzept, welches, übernommen in die Biomechanik bei einer mehrgelenkigen Bewegung, die Bewegung der einzelnen Glieder bzw. Gelenke in den Kontext der jeweils anderen Glieder und Gelenke stellt. Dabei unterscheidet man zwei Arten, nämlich offenen sowie geschlossenen kinematischen Ketten:

offene kinematische Kette: die einzelnen Glieder bzw. Gelenke bewegen sich unabhängig voneinander.
geschlossenen kinematische Kette: die einzelnen Glieder bzw. Gelenke bewegen sich zusammen, sprich die Bewegung eines bestimmten Gelenkes hat zugleich auch die Bewegung anderer Gelenke zur Folge.

Das Konzept der kinematischen Ketten geht auf den deutschen Ingenieur Franz Reuleaux (1829–1905) zurück, der das „Link-Konzept“ erstmals 1876 vorschlug. Ursprünglich sollte dies zur mechanischen Beschreibung und Funktionsweise von Maschinen dienen, weil mechanische Gesetzmäßigkeiten aber genauso für Bewegungen biologischer Systeme gelten, hat es sich mittlerweile zu einem allgemein akzeptierten Prinzip in der Biomechanik entwickelt.

Reuleaux folgerte zu seiner Zeit, dass in einem Verbindungssystem einer Reihe überlappender starrer Segmentente folglich auf das Einwirken einer externen Kraft jedes Segment Kraft aufnimmt und auf das benachbarte Segment überträgt, wodurch eine Kettenreaktion entsteht. Dadurch führt die Bewegung an jedem Gelenk zu einem vorhersehbaren Bewegungsmuster an allen anderen Gelenken in der Kette. Solch ein System beschreibt man heute als geschlossene kinematische Kette. Die Übertragung dieses Konzeptes auf die Analyse menschlicher Bewegungen wurde dann im 20. Jahrhundert, genauer gesagt in den 1930er Jahren vorgeschlagen, bis es dann schließlich in den 50er Jahren von Artur Steindler populär gemacht wurde. Steindler schlug vor, sich den menschlichen Körper als System starrer, überlappender Segmente vorzustellen. Er definierte die kinetische Kette als eine Kombination mehrerer hintereinander angeordneter Gelenke, die eine komplexe motorische Einheit bilden. Zum Beispiel kann jedes knöcherne Segment der unteren Extremität, wie Fuß, Unterschenkel, Oberschenkel und Becken, als starre Verbindung betrachtet werden, wobei die Knöchel-, Knie- und Hüftgelenke als Verbindungsgelenke fungieren. In späteren Schriften kategorisierte Steindler das Konzept der kinetischen Kette je nachdem, wie sich das terminale Segment verhält als offen oder geschlossen. Dabei entspricht eine offene kinematische Kette einer Kombination nacheinander angeordneter Gelenke, in denen sich das Endsegment frei bewegen kann, sprich ein freies Endglied vorhanden ist. Eine geschlossene kinematische Kette hingegen entspricht demnach einen Zustand oder eine Umgebung, in der das distale Segment auf erheblichen äußeren Widerstand trifft, der seine freie Bewegung verhindert oder einschränkt.

Was den Namen angeht, so ist zunächst zu erwähnen, dass man unter Kinetik die Untersuchung von Kräften versteht, welche die Bewegung eines Körpers beeinflussen. Im Gegensatz dazu ist die Kinematik die Untersuchung der räumlichen und zeitlichen Eigenschaften einer Bewegung ohne Berücksichtigung der verursachenden Kräfte. Steindler selbst verwendete den Begriff „kinetisch“ (Kräfte), während Ingenieure den Begriff „kinematisch“ (Bewegung) verwenden, auch wenn oftmals über dasselbe gesprochen wird. Der Ausdruck „Kinetische Kette“ wird in der Technik oder Robotik aber nicht verwendet, da kinematische Kette die technisch korrekte Bezeichnung ist. Dennoch wird der Begriff „kinetische Kette“ im biomechanischen Kontext auch häufig verwendet.

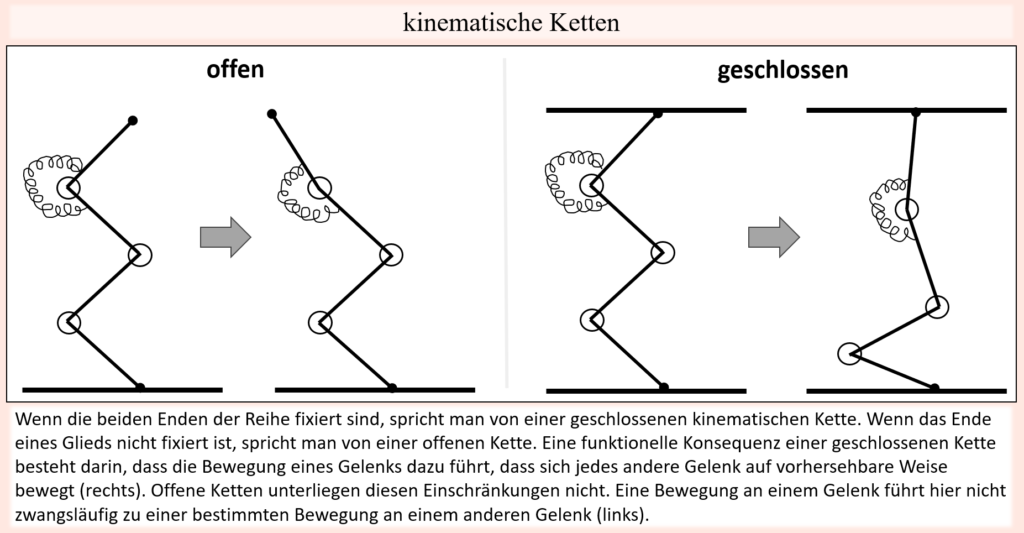
Betrachtet man verschiedene alltägliche oder auch sportliche Bewegungen des Menschen, dann wird man feststellen, dass einige davon geschlossen, andere offen und wieder andere zum Teil geschlossen bzw. offen sind. Hebt man zum Beispiel einfach nur den Arm an, dann ist dies offensichtlich eine offene kinematische Kette, schließlich bewegt sich der Arm frei im Raum und das Endsegment (also die Hand) ist nirgendwo fixiert bzw. wird anderweitig in seiner Bewegungsfreiheit eingeschränkt. Als Beispiel einer geschlossenen Kette wird hingegen oftmals eine frei ausgeführte Kniebeuge angeführt, wobei man hierbei aufpassen muss, weil die Kniebeuge mechanisch gesehen keineswegs einer gänzlich geschlossenen kinematischen Kette entspricht. Aber darauf kommen wir gleich zurück, wenn wir entsprechende Kniebeuge mit einer Beinpresse, einer tatsächlich geschlossenen kinematischen Kette, vergleichen. Tatsächlich sind Körperbewegungen meistens nicht gänzlich geschlossen, was wohl auch der Grund dafür ist, warum die Definition für offene und geschlossene kinematischen Ketten oft etwas unpräzise ist. So ist eben nicht wirklich klar, was es bedeutet, wenn dem Endsegment ein „erheblicher Widerstand“ entgegensteht. Für unsere Zwecke präzisieren wir diese Definition also, indem wir die obig erwähnte Unterscheidung verwenden, also davon ausgehen, dass in einer wirklich geschlossenen Bewegungskette die Bewegung eines Gelenkes zwangsweise auch bestimmte Bewegungen der anderen Gelenke mit sich zieht. Was diese Definition nämlich ermöglicht, ist es die funktionelle Rolle bestimmter Muskeln innerhalb der jeweiligen Bewegung besser nachzuvollziehen. Denn sogleich die Bewegung einzelner Gelenke in geschlossenen Ketten mit der Bewegung der anderen Gelenke in Verbindung steht, so gilt dies dementsprechend auch für Muskeln, sodass ein Muskel, welcher in einer offenen kinematischen Kette gemäß seinem anatomischen Verlauf lediglich die Bewegung eines bestimmten Gelenkes beeinflusst, in einer geschlossenen Kette auch die anderen Gelenke beeinflusst. Aber was bedeutet das? Nun, im Grunde erschwert es ausgehend von einer Bewegung und einwirkenden Kräften auf die muskuläre Belastung und Beteiligung zu schließen, weil die in einer offenen Bewegungskette vorherrschend klare Abgrenzung von Muskeln und Muskelfunktionen, bei geschlossenen Ketten nur noch bedingt gegeben sind. Aber sehen wir uns hierzu besagtes Beispiel einer Beinpresse an, denn damit sollte das Prinzip dahinter deutlich ersichtlich werden. In vorangehenden Abschnitten wurde anhand einer Kniebeuge bereits beispielhaft aufgezeigt, inwiefern eine unterschiedliche Bewegungsausführung Hebelverhältnisse, vor allem zwischen Hüftgelenke und Kniegelenke, verändern kann, was sich dann eben auch in der muskulären Beteiligung im Laufe der Bewegung zeigt. Steigt also der Hebelarm, den die Schwerelinie des Körpers auf die Kniegelenke ausübt, dann steigt hier auch das erzeugte „Flexions-Drehmoment“, weswegen der Quadrizeps als Kniestrecker ein entsprechend starkes Drehmoment erzeugen muss, um den Widerstand zu überwinden. Gleiches gilt für die Hüftmuskulatur. Wenn wir hierbei nun erstmal die zweigelenkigen Muskeln, welche sowohl über Knie-als auch Hüftgelenke ziehen, nämlich der Rectus femoris sowie die Hamstring-Gruppe, außen vorlassen, denn diese können Knie und Hüfte auch unabhängig von der kinematischen Kette bis zu einem gewissen Grad verbinden (worauf an einem späteren Punkt eingegangen wird), dann agieren Hüft- und Kniemuskeln anatomisch gesehen erstmal getrennt voneinander. Sprich, vor allem der Gluteus sorgt durch seine Kontraktion für eine Hüftstreckung und der Quadrizeps für eine Kniestreckung. In einer ganz normalen Kniebeuge ist das dann der Grund, weshalb die muskuläre Belastung bzw. Beteiligung grob abgeschätzt werden kann, indem die jeweilige Gelenkbelastung (bzw. das „Widerstandsdrehmoment“) betrachtet wird. Was nun aber bei einer geschlossenen Bewegungskette passiert, ist, dass die Gelenke, bei einer Beinpresse eben vor allem Hüft- und Kniegelenke, Teil einer Kettenreaktion werden. Dies wird ersichtlich, wenn man sich vor Augen führt, dass kein Endglied frei bewegt werden kann, sondern beide fixiert sind. Wenn der Trainierende z.B. in einer Beinpresse sitzt, dann ist sein Oberkörper durch den Sitz der Maschine fixiert und bewegt sich nicht. Gleiches gilt für die Füße, welche an der Beinablage fixiert sind. Um nun nachzuvollziehen, dass es sich tatsächlich um eine geschlossene kinematische Kette handelt, stellt man sich vor, dass der Trainierende bei besagter Beinpresse lediglich die Knie streckt oder lediglich die Hüftgelenke beugt. Dadurch, dass die Füße als auch der Oberkörper fixiert sind, erzeugt eine alleinige muskelinduzierte Hüftstreckung, gleichermaßen auch eine Kniestreckung und eine alleinige Kniestreckung auch eine Hüftstreckung.

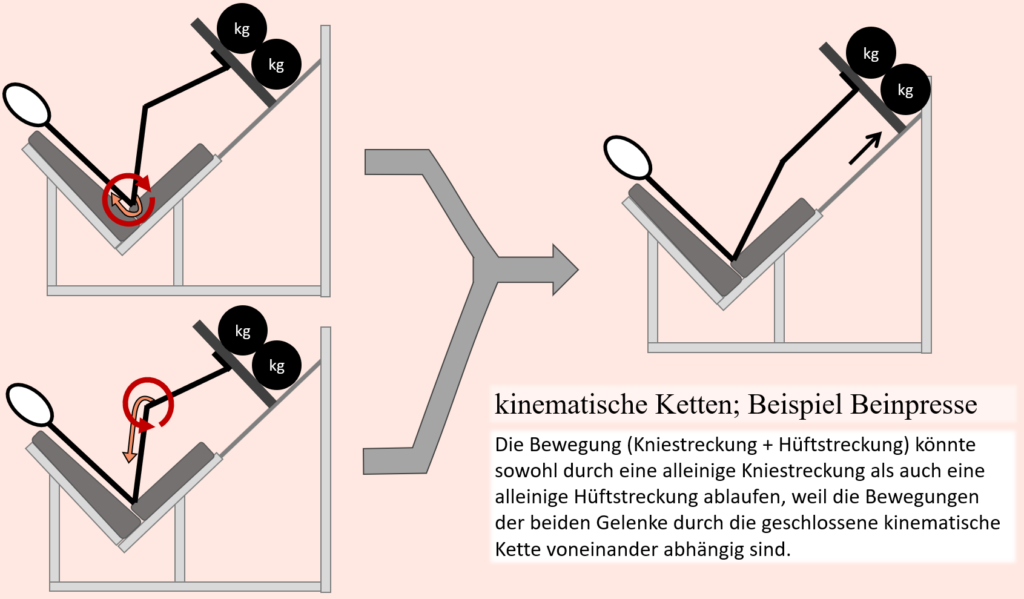
Hier wird dann auch ersichtlich, weshalb eine freie Kniebeuge keine gänzlich geschlossene Kette ist. Denn bei einer frei ausgeführten Kniebeuge sind zwar die Füße am Boden fixiert, der Oberkörper kann sich aber frei bewegen. Dies wird auch ersichtlich, wenn man sich hier mal vorstellt, dass der Trainierende nur die Knie oder nur die Hüfte aktiv bewegen würde, denn wohingegen dies im Falle der Beinpresse trotzdem zur gänzlichen Bewegung führen würde, ist dies bei einer freien Kniebeuge nicht, bzw. nur sehr begrenzt der Fall. So wird dem Oberkörper zwar ein gewisser Widerstand entgegengebracht, jedoch geht die Bewegung von Knie oder Hüfte eben nicht zwangsweise auch mit einer bestimmten Bewegung in den jeweils anderen Gelenken einher. Würde der Trainierende am Beginn der Konzentrik, also in der Hocke beispielsweise ausschließlich die Knie strecken, dann hätte dies keine Hüftstreckung zur Folge, sondern der Oberkörper würde schlichtweg nach vorne kippen. Um auch die Hüfte zu strecken, muss somit auch die Hüftmuskulatur involviert sein, welche jene Gelenkbewegung ermöglicht. Diesem Umstand kommt dann auch zu Schulden, dass bei besagter Beinpresse im Gegensatz zur Kniebeuge die muskuläre Involvierung weniger gut von der Bewegung abgelesen werden kann.

Wohlgemerkt bedeutet dies natürlich nicht, dass Hebelverhältnisse bei solch geschlossenen Ketten keine Rolle spielen würden, denn auch hier wird die Beteiligung der Muskeln wahrscheinlich damit grob korrelieren, vor allem wenn die Hebelverhältnisse sehr einseitig sind.

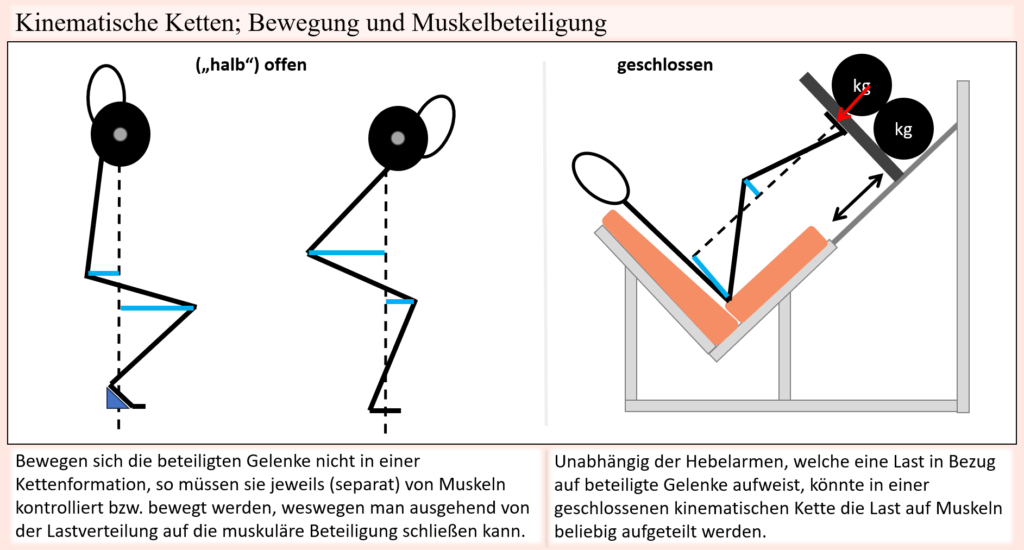
Nun ist dieses Thema rund um kinematische Ketten vor allem im Kontext von Trainingsmaschinen interessant, weil hierbei die Bewegung des Menschen eben oftmals von der Maschine vorgegeben wird, sodass gleichermaßen eine geschlossene Bewegungskette entsteht. Aber auch im Kontext von freien Hanteln finden sich vereinzelt geschlossene kinematische Ketten. Ein Beispiel hierfür wäre das Langhantelbankdrücken, wo sich unter Umständen ein Teil der Bewegung als kinematisch geschlossene Kette erweisen kann. Beginnen wir hierzu aber mit einer Betrachtung von Kurzhantel-Bankdrücken, denn hierbei handelt es sich um eine offene Bewegungskette. Der Grund hierfür ist auch ziemlich ersichtlich. So liegt der Trainierende zwar mit dem Rücken fixiert auf einer Bank, jedoch bewegen sich die Arme frei im Raum, wobei auf Händen unabhängig voneinander eine Last in Form einer Kurzhantel lastet. Die bei der Bewegung involvierten Gelenke, nämlich vor allem das Schulter- und Ellbogengelenk bewegen sich unabhängig, bzw. müssen getrennt von jeweiligen Muskeln kontrolliert werden. So sorgt vor allem der Pectoralis major für die horizontale Abduktion der Schulter, währenddessen die Ellbogenmuskulatur den Ellbogen stabilisiert und je nach Position verhindert, dass der Arm von der Last nicht ungewollt gestreckt oder gebeugt wird.

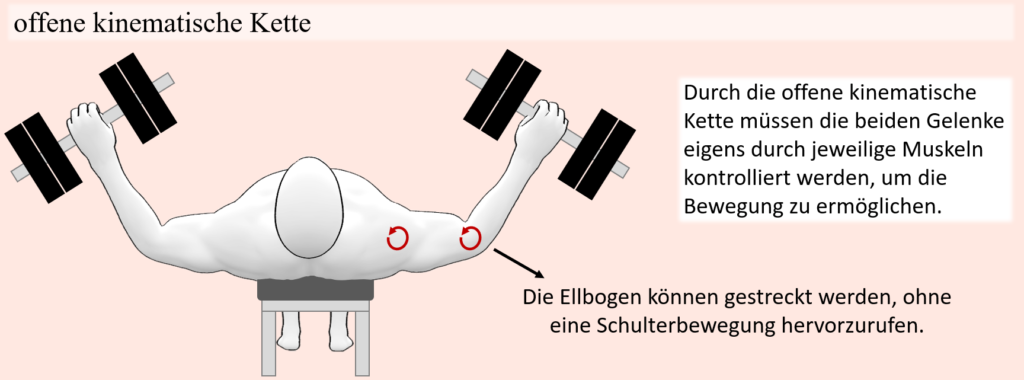
Wird die Bewegung nun aber mit einer Langhantel ausgeführt, dann sind zugleich beide Hände durch die Stange verbunden. Die Griffposition der Hände verändert sich dabei auch nicht und dadurch dass die Stange mit beiden Händen in Verbindung steht, können die Hände auch nicht wie etwa bei den Kurzhanteln unabhängig nach lateral bewegt werden, mit anderen Worten, die Hände sind an der Stange fixiert. Nun können sich die Hände samt Hantel an und für sich trotzdem relativ frei im Raum bewegen. Würde der Trainierende am Beginn der Konzentrik, also wenn die Stange auf der Brust aufliegt, nur die Ellbogen strecken, denn würden die Hände samt Stange Richtung Beine wandern, ohne dass eine Bewegung im Schultergelenk stattfindet (je nach Ausführung ist dies nicht zwingend der Fall, es wird aber die Regel sein). Das zeigt, dass die Bewegung zumindest meistens nicht gänzlich geschlossen ist. In einer ganz bestimmten Situation aber, nämlich genau dann, wenn sich die eine Bewegungsachse des Ellbogens in etwa auf eine Linie mit der Hantel und den Schultergelenken befindet, dann entsteht eine geschlossene kinematische Kette, in der eine Ellbogenstreckung gleichzeitig auch mit der horizontalen Abduktionsbewegung des Oberarmes einhergeht und umgekehrt. In diesem speziellen Fall nämlich würde eine Ellbogenstreckung die Hände nach lateral, also nach außen Bewegen, dadurch dass diese aber an der Hantel fixiert sind, kann die Ellbogenstreckung nur erfolgen, wenn auch eine horizontale Adduktionsbewegung stattfindet und umgekehrt. Dementsprechend kann in dieser Situation der Brustmuskel die Streckbewegung des Ellbogens hervorrufen, bzw. diese unterstützen und umgekehrt der Trizeps die horizontale Adduktionsbewegung des Schultergelenkes. Dabei ist es einigen wenigen Athleten sogar möglich, über die gesamte Bewegung hinweg diese geschlossene Kette aufrechtzuerhalten.

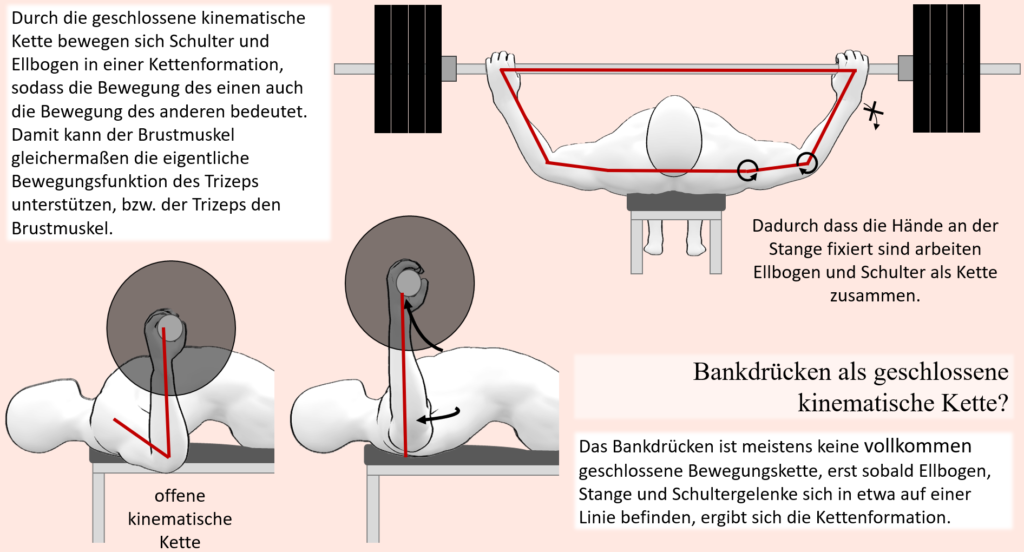
Auch im Falle des weiter oben angesprochenen sumo-Kreuzhebens bzw. sumo-Kniebeugens kann zumindest zum Teil eine geschlossene Bewegungskette entstehen. Und zwar können durch den breiten Stand, was gleichermaßen eine Außenrotation der Beine mit sich zieht, die Knie und die Hüftgelenke in eine Kettenformation gebracht werden, sodass die Kniestreckung, weil die Füße am Boden fixiert sind, auch eine Hüftstreckung mit sich ziehen und umgekehrt eine Hüftstreckung zugleich eine Kniestreckung erzeugen kann. Wohlgemerkt handelt es sich hierbei aber keineswegs um eine mechanisch vollkommen geschlossene kinematische Kette, was ersichtlich wird, wenn man die Bewegung von der Seite betrachtet.

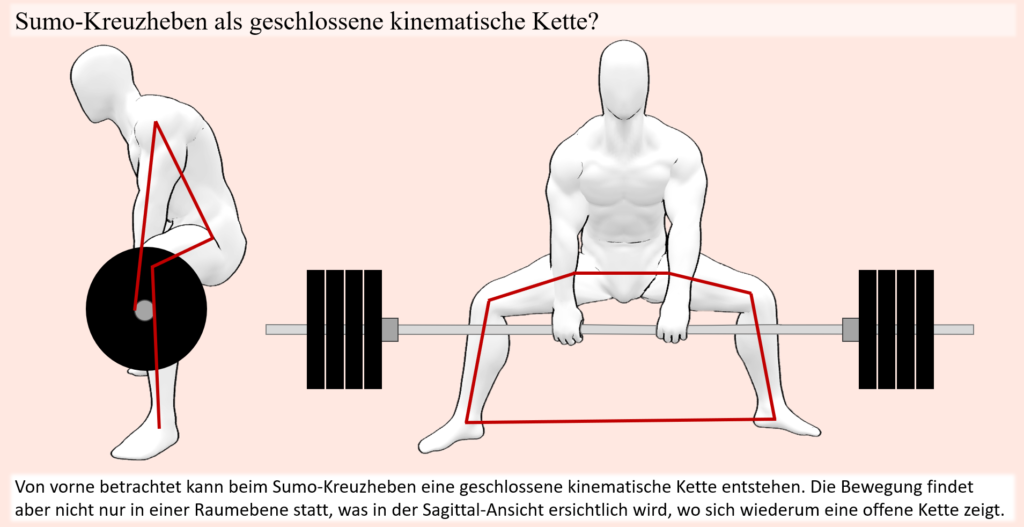
Architektur des Skelettmuskels (Fiederungswinkel)

Die grundlegenden Krafterzeugungseigenschaften der Muskelfaser samt den entsprechenden Mechanismen im Hintergrund wurden in obigen Abschnitten bereits aufgezeigt, wie aber im Kontext der Muskel-Sehnen-Einheit bereits kurz angesprochen, sind diese Muskelfasern in Muskeln zusammengefasst. Die mechanischen Eigenschaften des Muskels entsprechen aber keineswegs einfach nur der schlichten Summe seiner Bestandteile, sondern vielmehr ebenso in der Art und Weise, wie der Muskel aufgebaut ist. Genauer gesagt geht es vor allem auch darum, wie die Muskelfasern innerhalb eines Muskels orientiert sind. Zunächst würde man vielleicht vermuten, dass die einzelnen Fasern eines Muskels immer von Muskelursprung Richtung Muskelansatz verlaufen, was auch bei einigen Muskeln der Fall ist. In den meisten Fällen aber sind die Muskelfasern in einem bestimmten Winkel im Verhältnis zur Muskelachse (gedachte Linie zwischen Muskelansatz und Muskelursprung) orientiert. Und diese Orientierung hat direkt Auswirkungen auf die mechanischen Eigenschaften des Muskels. Vereinfachend unterscheidet man also zwischen zwei Faseranordnungen. Muskeln, deren Fasern (annähernd) in Richtung der Wirkungslinie der Muskelachse ausgerichtet sind, werden als parallel faserige Muskeln bezeichnet. Muskeln, deren Fasern hingegen einen Winkel mit der Achse bilden, werden als gefiederte Muskeln bezeichnet.

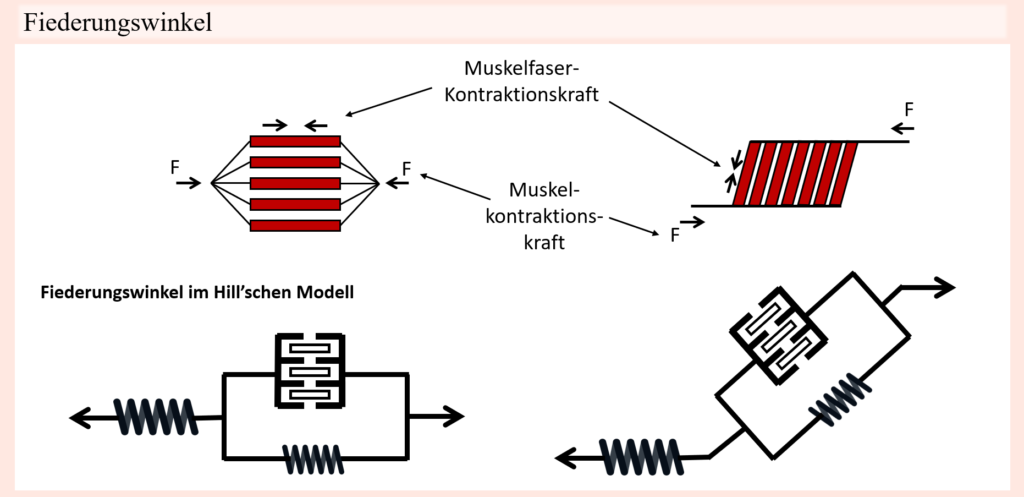
Im Grunde kann man hieraus auch bereits wesentliche mechanische Auswirkung solch einer Fiederung im Vergleich zu keiner (bzw. sehr geringer) Fiederung ableiten. Verlaufen die Fasern, welche den Muskel bilden, entlang der Muskelachse, so beschreibt die Längenänderung des Muskels gleichermaßen die Längenänderung der Fasern und die aktive Kraft des Muskels ist gleich die Summer der Kräfte der Fasern. Die mechanischen Eigenschaften gefiederter Muskeln sind hingegen komplexer, da die geometrische Anordnung das Verhältnis zwischen Längenänderung der Fasern und Längenänderung des gesamten Muskels beeinflusst. Auch bei gefiederten Muskeln wirkt die Muskelkraft entlang der Achse, also in Sehnenrichtung, verlaufen die einzelnen Fasern aber in einem Winkel dazu, dann wirkt nur ein Teil der von ihnen erzeugten Kraft in jene Richtung.

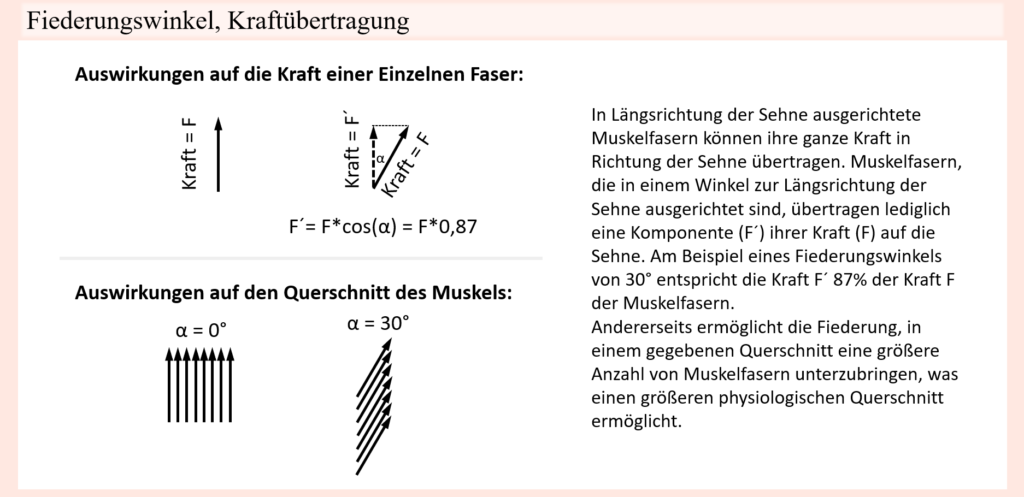
Dementsprechend ist die in Richtung der Sehne wirkende Kraft eines gefiederten Muskels immer kleiner als die Kraft seiner Muskelfasern. Das wiederum bedeutet aber nicht, dass gefiederte Muskeln schwächer wären, ganz im Gegenteil. Denn was ist überhaupt der Grund für diese Fiederung, wenn daraus folgt, dass ein Teil der entwickelten Kraft für die Kraft des Muskels nicht genutzt wird? Die Antwort ist ziemlich einfach, nämlich Platz. Muskeln des menschlichen Körpers sind im Regelfall mechanisch benachteiligt, was deren Hebelarm im Vergleich zum Hebelarm der gegen wirkenden Lasten betrifft. Daraus folgt, dass Muskeln meistens deutlich mehr Kraft erzeugen müssen als die Kraft, der sie eigentlich entgegenwirken. Und wie schafft man es, dass ein Muskel viel Kraft erzeugt? Richtig, durch viele parallel ablaufende Querbrücken, was durch viele parallele Fasern erreicht wird. Bei einem Fiederungswinkel gleich null gäbe es dementsprechend oftmals Schwierigkeiten, genügend kräftige Muskeln unterzubringen, weil mit einer großen Zahl von parallel zur Längsachse des Muskels angeordneten Fasern der anatomische Querschnitt unzulässig groß werden würde (mehr parallel/nebeneinander vorhandene Fasern machen den Muskel dicker). In gefiederten Muskeln, wo die Fasern hingegen einen Winkel mit der Sehne bilden, kann eine variable Zahl von Fasern längs einer Sehne ansetzen, ohne den anatomischen Querschnitt überaus zu erhöhen. Die Fiederung reduziert folglich die Größe des erforderlichen anatomischen Querschnitts auf Kosten der Kraftentfaltung. Die größere Anzahl an Fasern, die untergebracht werden kann, sorgt aber dann dafür, dass gefiederte Muskeln letztlich in Summe trotzdem mehr Kraft entfalten können, auch wenn nicht die vollständige Kraft der einzelnen Fasern zur Kontraktion in Richtung der Längsachse verwendet wird. Genau aus diesem Grund ist der anatomische Querschnitt allein kein besonders guter Messwert, um hiervon auf mechanischen Eigenschaften, wie die Muskelkraft zu schließen. Um die Abmessungen eines Muskels tatsächlich mit der Kraft in Verbindung zu bringen, bedarf es des sogenannten physiologischen Querschnittes eines Muskels. Dieser beschreibt die Summe der Flächen aller (senkrecht zu ihrer Länge geschnittenen) Muskelfasern eines Muskels und bezieht damit tatsächlich den Querschnitt der einzelnen Fasern mit ein. Dementsprechend ist der physiologische Querschnitt eines Muskels auch proportional zu dessen maximalen tetanischen Kraft.

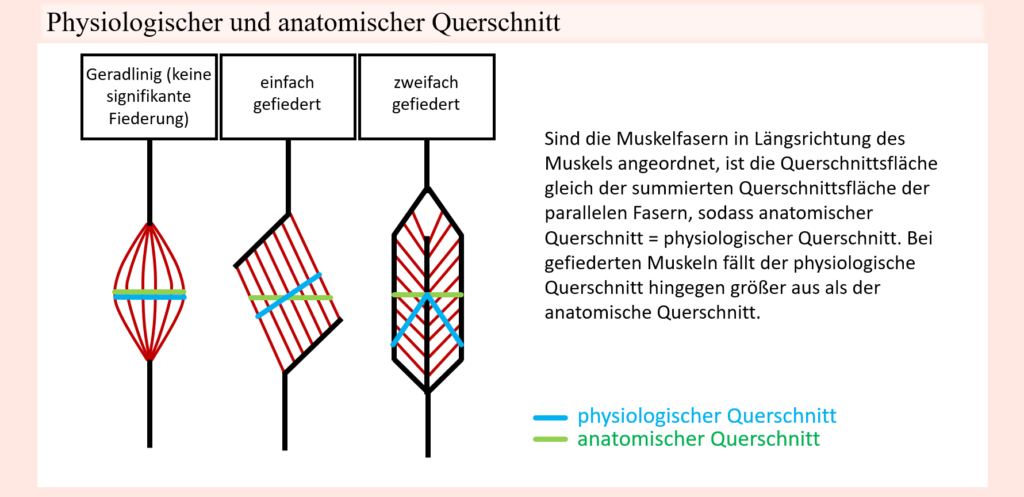
Bei Vernachlässigung feinerer Unterschiede kann man hierbei einige allgemein gültige Aussagen treffen. Muskeln mit einem größeren Fiederungswinkel bestehen im Allgemeinen aus mehr Fasern und können folglich größere Kräfte entfalten. Muskeln mit einem kleinen Fiederungswinkel haben hingegen den Vorteil einer besseren Kraftausbeute bei der Übertragung der Faserkraft auf die Sehne. Ebenso sind Muskelfasern, welche entlang der Längsachse verlaufen, in der Regel länger als Fasern von gefiederten Muskeln. Muskeln mit langen Muskelfasern wiederum haben einen großen Bereich der Längenänderung, da der Bereich der Längenänderung proportional zur Faserlänge wächst, schließlich geht dies direkt auf die Anzahl hintereinander (seriell) angeordneter Sarkomere zurück. Die Längenänderung wächst damit mit abnehmendem Fiederungswinkel an. Im Allgemeinen ist die Architektur der Muskeln an die jeweiligen mechanischen Erfordernisse angepasst. So weisen gerade Muskeln mit langem Hebelarm längere Muskelfasern auf, denn bei einer Gelenksdrehung um ein gegebenes Winkelintervall ändert sich die Länge des Muskels mit kleinem Hebelarm nämlich aus rein geometrischen Gründen weniger als die Länge des Muskels mit großem Hebelarm.

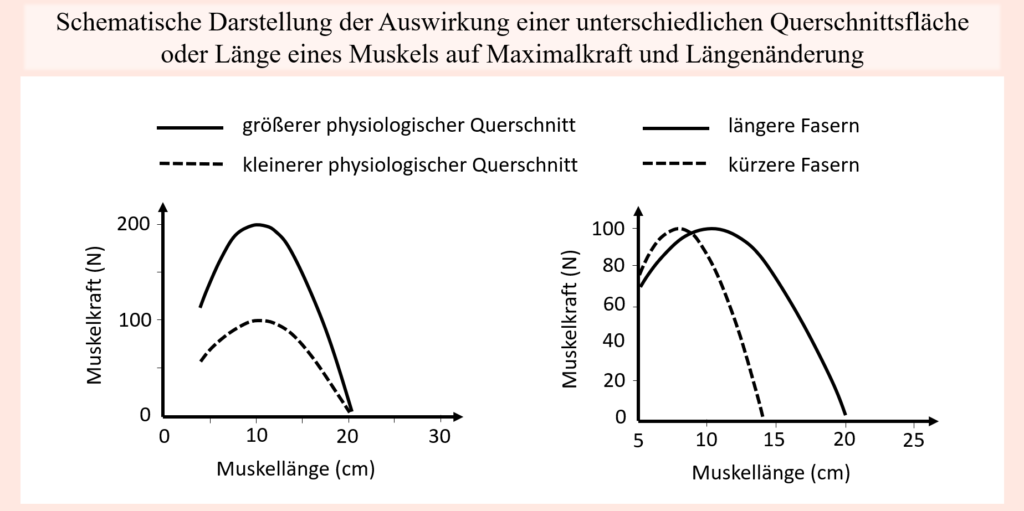
Was die Verkürzungsgeschwindigkeit angeht, verkürzen längere Muskelfasern der höheren seriellen Sarkomeranzahl wegen schneller als kürzere, jedoch überträgt sich dies nicht einfach so auf gefiederte und nicht-gefiederte Muskeln, weil die Fasern eines gefiederten Muskels im Laufe der Kontraktion rotieren, sodass der Fiederungswinkel ansteigt. Hierbei entsteht ein Weggewinn, wobei die Längenänderung des ganzen Muskels größer ausfällt als die Längenänderung der Fasern, ein Phänomen welches man als „muscle gearing“ bezeichnet. Die Faserrotation verringert die Ausgangskraft eines Muskels, erhöht aber die Geschwindigkeit, indem sie es dem Muskel ermöglicht, in einem höheren Übersetzungsverhältnis (Muskelgeschwindigkeit/Fasergeschwindigkeit) zu arbeiten. Das Ausmaß der Faserrotation und damit das Übersetzungsverhältnis hängen davon ab, wie der Muskel seine Form im Laufe der Kontraktion ändert.

Orientierung der Fasern in Bezug zur Muskel-Längsachse

funktionelle Merkmale

annähernd parallele Anordnung der Fasern,

Fiederungswinkel <10°

Übertragung der gesamten Faserkraft auf die Sehne
größerer Bereich der Längenänderung
Muskelfaser- intrinsisch höhere Verkürzungsgeschwindigkeit.

Faserrichtung abweichend

von Muskelrichtung,

Fiederungswinkel >20°

Größerer physiologischer Querschnitt und damit größere Kraft
„muscle gearing“ verschafft schnellere Muskelverkürzung im Vergleich zur Faserverkürzung

Laterale Kraftübertragung

Muskelfasern haben intrinsische Krafterzeugungseigenschaften, welche sich aus Eigenschaften wie der Menge an parallelen und seriellen Sarkomeren ergeben. Diese Eigenschaften, auch wenn sie die Grundlage der muskulären Kraftproduktion bilden, lassen sich aber nicht einfach auf den Muskel übertragen. Ein wesentlicher Grund dafür, neben dem Fiederungswinkel, welcher besagt wie die einzelnen Fasern innerhalb des Muskels orientiert sind, ist auch die Art und Weise wie die von den Sarkomeren erzeugten Kräfte weitergeleitet werden. Dazu werden die in den Sarkomeren erzeugten Kräfte über die Sarkomere in Reihe sowie das intramuskuläre Bindegewebsnetzwerk auf den myotendinösen Übergang übertragen. Dort sind die im Bindegewebe eingebetteten Muskelfasern ineinandergreifend mit den Kollagenfasern verbunden, die schließlich die Sehne bilden. Anders als man vielleicht meinen mag, werden die Kräfte einer Muskelfaser dabei nicht nur längs ihrer Achse übertragen, sondern Kräfte werden ebenso lateral auf extrazelluläre Bindegewebsstrukturen übertragen und von dort aus weitergeleitet. Diese laterale Kraftübertragung erfolgt durch das Zusammenspiel von Zwischenfilamenten, wie Desminfilamenten, welche Myofibrille innerhalb einer Faser quervernetzen und durch die Verbindungen der außen gelegenen Myofibrillen zu sogenannten Costameren, die sich in der Muskelzellmembran befinden und die Kraftübertragung auf die extrazelluläre Matrix ermöglichen. Die ersten Hinweise auf diese laterale Kraftübertragung und deren funktionelle Rolle für die Muskulatur ergaben sich durch Beobachtungen, in denen in Experimenten die direkten Verbindungen von einem gewissen Teil der Muskulatur von der Gelenksehne durchtrennt wurden, daraufhin die Kraft in Relation zur Kraft eines intakten Muskels, aber nicht verhältnismäßig dazu abfiel, sondern erstaunlich hochgehalten wurde. Heute scheint es so, dass die laterale Kraftübertragung sogar einen größeren Teil (70-80 %) ausmacht als die in Längsrichtung übertragene Kraft und dass sie eine biomechanische Notwendigkeit ist, um die Muskelintegrität aufrechtzuerhalten und die Kontraktionseffizienz zu verbessern. Erstens trägt es dazu bei, die Kontraktionskräfte über die gesamte Oberfläche der Muskelfasern zu verteilen, weil die einzelnen Myofibrille ihre Kraft so auch auf andere Myofibrille weitergeben, was die mechanische Belastung reduziert und die Fasern vor Überdehnung schützt. Zweitens trägt die laterale Kraftübertragung durch Costamere dazu bei, einheitlichere Sarkomerlängen aufrechtzuerhalten. Das gilt auch für Sarkomere in anderen Muskelfasern. Wenn eine Muskelfaser aktiv kontrahiert und eine benachbarte nicht, dann helfen die lateralen Querverbindungen dabei, dass sich auch diese zweite Muskelfaser verkürzt. Ebenso bietet die laterale Kraftübertragung einen Mechanismus, mit dem weiterhin Kraft von Muskelfasern erzeugt und übertragen werden kann, die aufgrund von Mikrotrauma oder während des Muskelwachstums unterbrochen sind.

Die mechanischen Eigenschaften der Skelettmuskulatur hängen also sowohl von den Eigenschaften der Muskelfasern und der extrazellulären Matrix als auch von der Wechselwirkung zwischen den beiden ab. Kontraktile Kräfte werden seitlich im intramuskulären Bindegewebe auf das Epimysium und dann auf die Sehne übertragen.

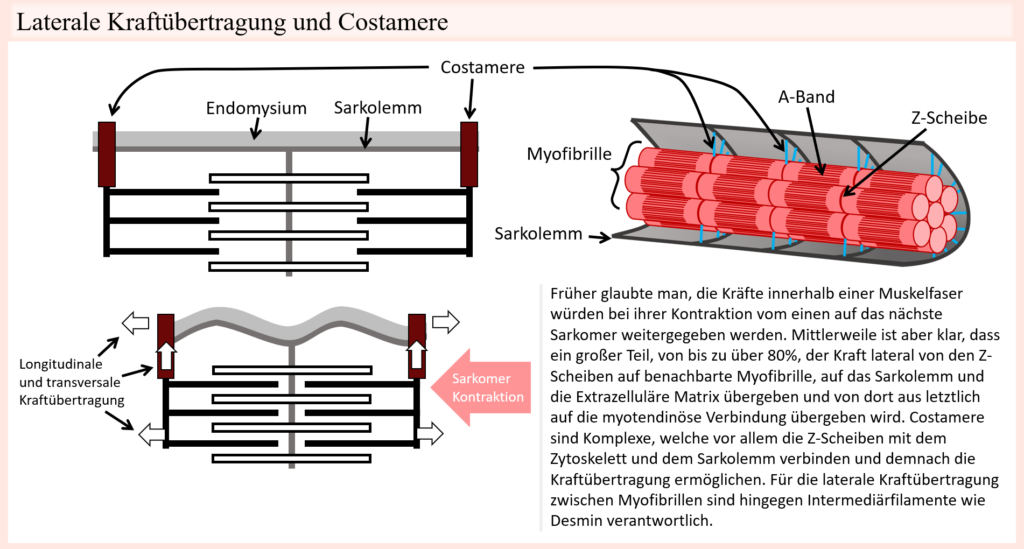
Die laterale Kraftübertragung wirkt sich auch positiv auf die maximale Krafterzeugung aus. Normalerweise tragen die Sarkomere einer Kette nämlich nicht zur Maximalkraft bei, weswegen es die erzeugbare Maximalkraft auch nicht beeinflusst, wenn mehr oder weniger Sarkomere in Serie geschaltet sind. Wird nun aber die generierte Kraft eines in Sarkomers innerhalb einer Reihe lateral auf andere Myofibrille und schließlich auf die extrazelluläre Matrix und von dort auf die Sehne übertragen, dann kann dies die Kraft durchaus steigert. Die Kraft wird quasi aus der Kettenformation herausgenommen, und zieht über die extrazelluläre Matrix und anderen Myofibrillen parallel zur Kraft, welche in Längsrichtung auf die Sehne weitergegeben wurde. Das bedeutet, durch laterale Verbindungen über Costamere wird quasi eine zusätzliche Ebene der parallelen Kraftübertragung erreicht, was vermutlich ähnliche Effekte mit sich zieht wie tatsächlich mehr parallel angeordnete Sarkomere, welche die Maximalkraft anheben.

Andererseits reduziert die laterale Kraftübertragung wohl auch etwas die Verkürzungsgeschwindigkeit. Aufgrund der erhöhten seitlichen Verbindungen stoßen die Myosinköpfe nämlich auf größeren Widerstand, wenn sie versuchen, Querbrückenzyklen zu durchlaufen. Durch diesen zusätzlichen Widerstand nimmt die Muskelkontraktionsgeschwindigkeit ab.

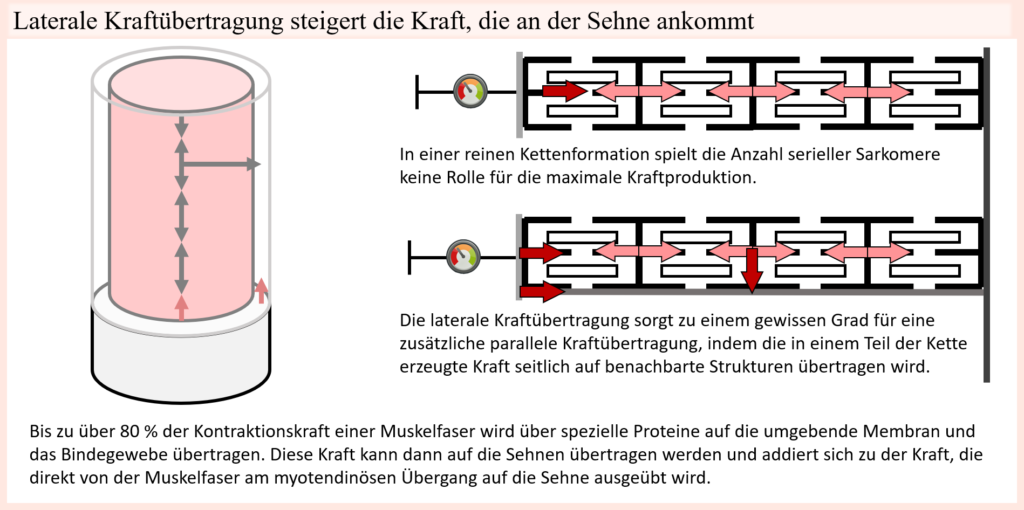
Aufgaben der Skelettmuskulatur und Kontraktionsformen

Skelettmuskeln erfüllen im Bewegungsapparat in enger Zusammenarbeit mit anderen Elementen, wie den Sehnen, die Aufgabe, Bewegungen zu kontrollieren. Kontrollieren bedeutet hier zum einen natürlich das Auslösen bzw. Initiieren von Bewegungen, andererseits aber ebenso das Abbremsen oder Verhindern von Bewegungen, wenn von außen auf den Körper einwirkenden Kräften entgegengehalten werden muss. Um diese Aufgabe zu erfüllen, produzieren sie Kraft, indem sie aktiv kontrahieren, wobei in den obigen Abschnitten die wesentlichen Mechanismen hinter dieser Kontraktion, der mechanische Aufbau, als auch vor allem die daraus resultierenden mechanischen Eigenschaften und Funktionen beschrieben wurden. All diese beschriebenen Aspekte und Mechanismen tragen letztlich ihren Teil bei, dass die Skelettmuskulatur so funktioniert, wie sie es tut. Wohlgemerkt lag hierbei der Fokus auf der zugrunde liegenden Muskel-Mechanik, weswegen auf Aspekte wie die Aktivierung, Kraftdosierung, Fasertypen oder gar Anpassungen nicht weiter eingegangen wurde. All diese Aspekte haben dann entweder kleinere Änderungen, bzw. Anpassungen der hier aufgezeigten mechanischen Elemente zur Folge, oder bestimmen darüber, in welchem Ausmaß diese verwendet werden.

Auch wenn das Skelettmuskelsystem selbst durchaus komplex ist und auch ein einzelner Muskel aus mechanischer Sicht einen vielschichtigen Komplex darstellt, so ist die Arbeitsweise von Skelettmuskeln ziemlich simpel. Durch ihre Kontraktion üben sie Kraft auf Sehnen und Knochen aus und kontrollieren damit Bewegungen. Diese Kontraktionskraft wirkt entlang der Muskelachse und wirkt immer verkürzend für den Muskel. Das bedeutet natürlich nicht, dass ein Muskel sich auch immer verkürzt, wenn er kontrahiert, sondern dass die erzeugte Kraft immer in jene Richtung gerichtet ist. Ein Muskel kann also nicht an einem Knochen drücken, indem er sich ausdehnt, sondern er übt stets Zugkraft aus. Die Summe der auf das Skelett einwirkenden Kräfte entscheidet dann im Grunde darüber, ob überhaupt und, wenn ja, was für eine Bewegung resultiert und ob sich der Muskel dann tatsächlich verkürzt, seine Längenposition beibehält, oder sogar verlängert wird.

In diesem Sinne können Muskeln entweder statisch oder dynamisch arbeiten. Unter statischer Muskelarbeit versteht man eine Kontraktion, bei der ein Muskel seine Länge nicht ändert, wohingegen man unter dynamischer Muskelarbeit eine Kontraktion versteht, bei der ein Muskel seine Länge ändert. Muskelkontraktionen lassen sich in drei Klassen einteilen:

Isometrische Kontraktion: Wenn ein Muskel Kraft erzeugt, dies jedoch keine Bewegung erzeugt, also der Muskel seine Länge nicht verändert, besteht ein statisches Gleichgewicht. Eine solche Kontraktion wird als isometrisch bezeichnet. Meistens wird diese Bezeichnung auch im erweiterten Sinne verwendet, sodass es auch als isometrische Kontraktion bezeichnet wird, wenn keine Gelenksbewegung stattfindet und somit die Muskel-Sehnen-Einheit ihre Länge beibehält. In diesem Fall verkürzt sich der Muskel jedoch sehr wohl, während sich seine Sehne entsprechend verlängert.
Konzentrische Kontraktion: Wenn der Muskel durch seine Kontraktion in der Lage ist sich zu verkürzen, wird es als konzentrische Kontraktion bezeichnet. Bei konzentrischen Kontraktionen ist, der Verkürzungsgeschwindigkeit wegen, die Muskelkraft immer geringer als die maximale isometrische Kraft. Arbeitet der Muskel gegen einen kleinen Widerstand, sodass das vom Muskel erzeugte Drehmoment im Gelenk deutlich stärker ist als das Drehmoment einer eventuellen Last, dann kann sich der Muskel mit größerer Geschwindigkeit verkürzen. Das bedeutet, je geringer der Widerstand, desto höher die Verkürzungsgeschwindigkeit, wobei maximale Kontraktionsgeschwindigkeit bei kleinstmöglichen Widerstand erreicht wird.
Exzentrische Kontraktion: Wenn der Muskel kontrahiert, also Kraft erzeugt, er dadurch aber nicht seine Länge vermindern oder konstant halten kann, also der kontrahierende Muskel gedehnt wird, dann spricht man von exzentrischer Kontraktion. Bei einer exzentrischen Kontraktion kann die Kraft auf den Muskel erheblich größer sein als die maximale isometrische Kraft F. Dies liegt daran, dass der Muskel der äußeren Kraft nicht nur seine aktiv erzeugte, sondern vielmehr die Summe seiner aktiven Kraft und der passiven, durch die Dehnung verursachten Rückstellkräfte entgegensetzen kann.

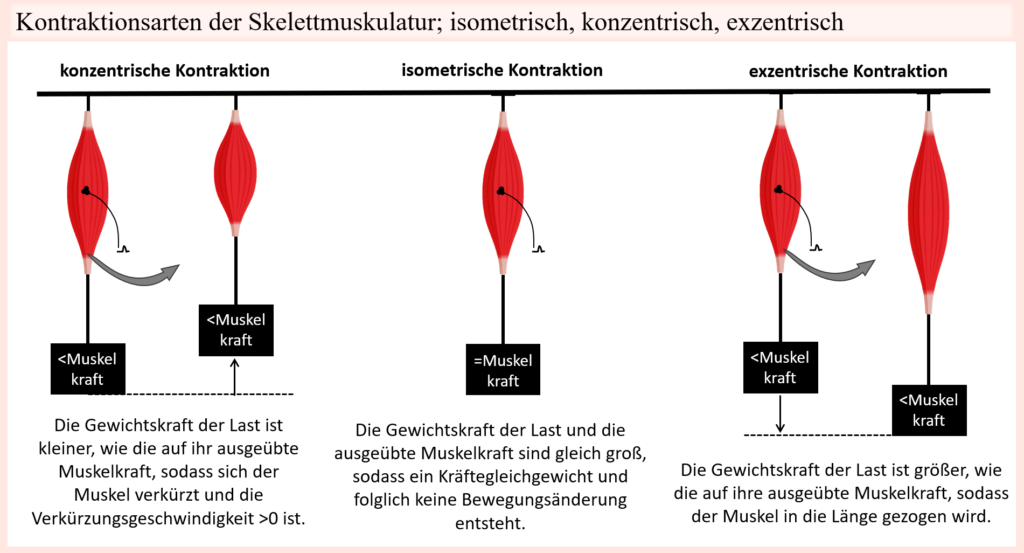
Vereinzelt werden zudem noch weitere Kontraktionsformen mit bestimmten Eigenschaften unterschieden.

Eine isotonische Kontraktion tritt auf, wenn ein Muskel bei konstanter Kraftentwicklung seine Länge ändert.
Eine isokinetische Kontraktion erfolgt, wenn der Muskel mit konstanter Geschwindigkeit kontrahiert.
Bei einer auxotonischen Kontraktion ändert sich die Länge und die Kraft.
Und bei der plyometrischen Kontraktion handelt es sich um eine explosive konzentrische Kontraktion, der unmittelbar eine exzentrische Kontraktion vorausgeht.

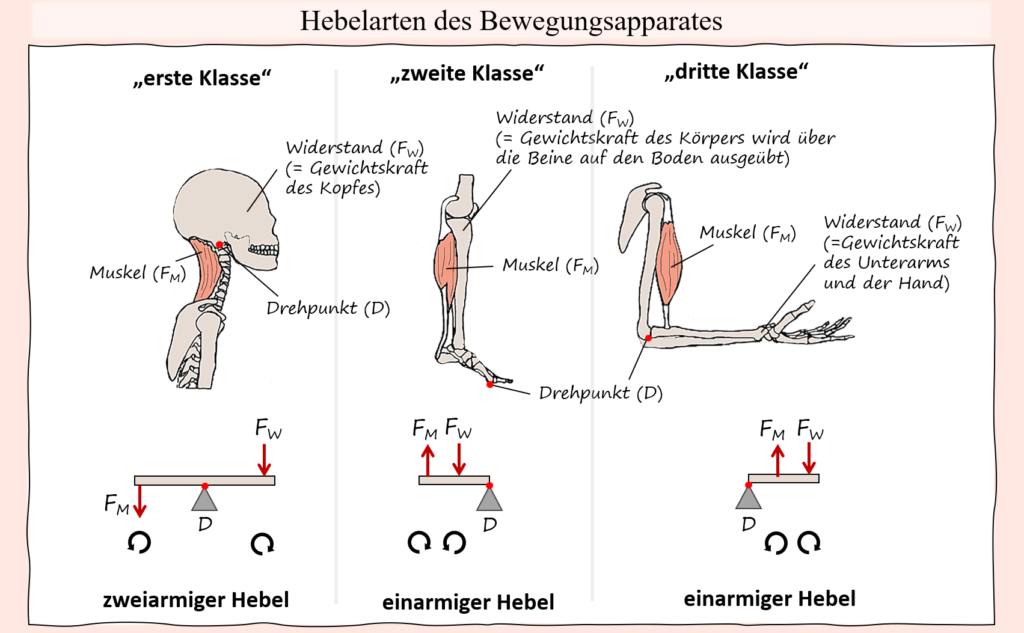
Alternativ kann auch eine Differenzierung in ein- und zweiarmigen Hebeln gemacht werden. Bei einem einarmigen Hebel greifen Muskelkraft und Last auf derselben Seite an, wohingegen bei einem zweiarmigen Hebel, die Muskelkraft und die Last auf gegenüberliegenden Seiten des Drehzentrums angreifen.

Die auf ein Gelenk einwirkenden Kräfte (seien es Muskel- und Bandkräfte oder z.B. Körpergewicht bzw. Schwerkraft) bewirken in diesem Sinne eine Gelenkbewegung (über das Drehmoment), wenn sie außerhalb des Drehzentrums, über einen Hebelarm, angreifen. Ebenso erzeugen sie aber auch eine translations-Kraft (was als Gelenkdruck wirken kann). Das ist nicht nur der Fall, wenn die Kräfte durch den Drehpunkt verlaufen, sondern auch bei einer, abseits vom Drehpunkt einwirkenden Kraft kann per Kräftezerlegung die Teilkraft ermittelt werden, die durch den Drehpunkt wirkt. Ein Sonderfall dabei sind sogenannte Kraftpaare, oder „force couples“, welche ausschließlich eine Drehbewegung auslösen. Das Kräftepaar besteht aus zwei gleich großen Kräften, die zueinander parallel sind, aber in zwei entgegengesetzte Richtungen wirken. Die Folge ist, dass ein Kräftepaar, das auf einen starren (nicht deformierbaren) Körper wirkt, dessen Massenmittelpunkt nicht verschieben kann, weil die translatorisch wirkende, resultierende Kraft gleich null ist, stattdessen können sie den Körper nur drehen. Im Allgemeinen sind Muskeln des Bewegungsapparates für die Erzeugung von Kräften und Drehmomenten verantwortlich, was sowohl zu Translations- als auch zu Rotationsbewegungen führt. Es gibt jedoch Beispiele im menschlichen Körper, in denen zwei oder mehr Muskeln zusammenarbeiten, um ein Drehmoment zu erzeugen, wie zum Beispiel der obere Trapezius und der Serratus anterior. Obwohl diese Muskeln keine identische Größe oder Ausrichtung haben, wird diese Situation häufig näherungsweise als Kräftepaar bezeichnet.

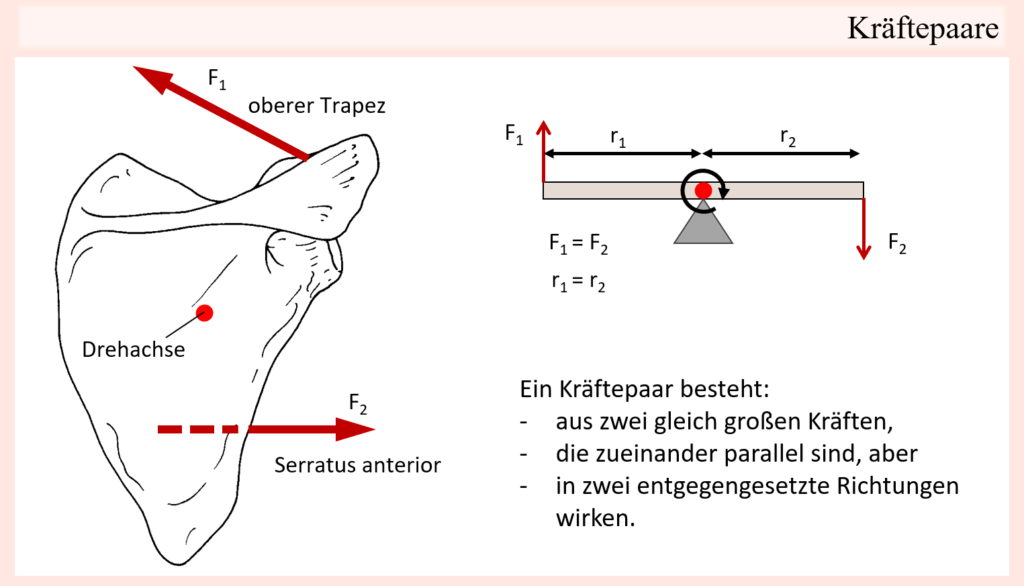
Muskeln und Drehmomente

Die Muskelkraft ist eine der zentralen Größen, wenn es um die Bewegungsfunktion und Effizienz (im Sinne des erzeugten Drehmoments) eines Muskels geht. Dabei gilt es im Wesentlichen drei wichtige Parameter zu berücksichtigen:

Kraftrichtung
Größe (Betrag der Kraft)
Angriffspunkt

Mit einer gewissen Sorgfalt ist es möglich, Orientierung und Wirkungslinie anhand von Leichen oder bildgebenden Verfahren wie der Magnetresonanztomographie (MRT) und der Computertomographie (CT) zu messen. Diese beiden Variablen sind für die Biomechanik besonders wichtig, weil anhand hiervon auf den Hebelarm eines Muskels in Bezug auf ein Gelenk geschlossen werden kann. Ebenso kann daraus geschlossen werden, inwiefern sich der Hebelarm und damit das vom Muskel erzeugte Drehmoment bei unterschiedlichen Gelenkwinkeln verändert, worauf wir weiter unten nochmal zurückkommen werden. Wohlgemerkt braucht man keine solchen aufwändigen Mittel zur Hand ziehen, um Angriffspunkte, Wirkungskraftlinien und folglich Hebelarme von Muskeln abschätzen zu können, aber gewisse Feinheiten können dadurch deutlicher gemacht werden. Wenn man beispielsweise zwei Muskeln betrachten, welche zur Abduktion des Armes beitragen, nämlich der seitliche Teil des Deltoids sowie der Supraspinatus. Beide Muskeln überspannen das Gleonohumeralgelenk und unterstützen bei ihrer Kontraktion die seitliche Abspreizung des Armes. Der Supraspinatus verläuft als Teil der Rotatorenmanschette aber unterhalb des Deltoids, weswegen man auch einen entsprechend kürzeren Hebelarm auf das Schultergelenk vermuten könnte. Bezieht man nun aber die Angriffspunkte, also die Ansatzpunkte der Muskeln am Oberarmknochen, sowie der Wirkungslinie mit ein, dann wird man feststellen, dass die beiden Muskeln vergleichbar lange Hebelarme aufweisen. (Der Muskelgröße wegen wird der Supraspinatus aber weniger Kraft erzeugen können, weswegen der seitliche Deltoid letztendlich trotzdem mehr zur Abduktion beiträgt.)

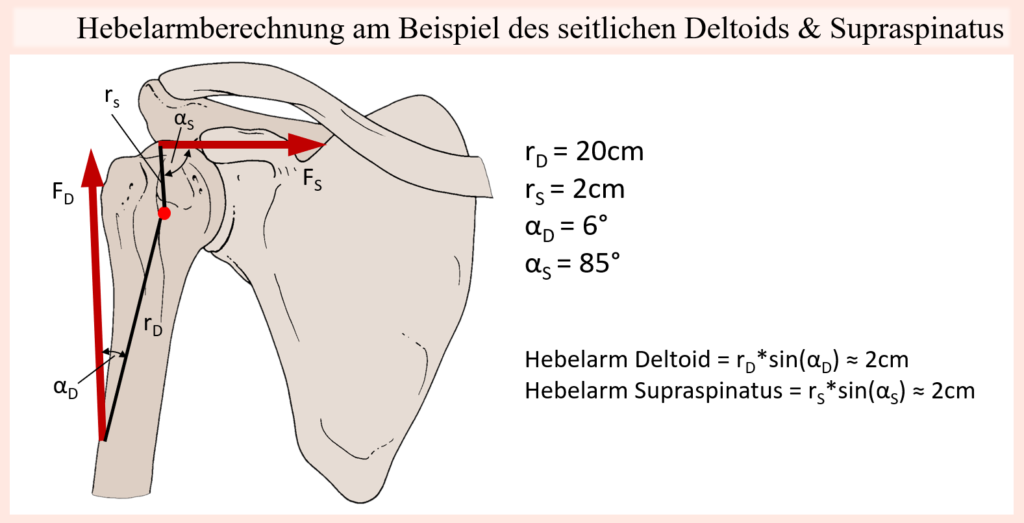
Was hingegen den Betrag der Muskelkraft angeht, ist das Ganze schon schwieriger, weil es sich hierbei um einen variablen Betrag handelt. Und variabel bedeutet hier nicht nur zwischen Individuen, sondern dass die Krafterzeugung beim selben Muskel in unterschiedlichen Gelenkpositionen und Kontraktionseigenschaften variiert. So variiert zum einen die von einem Muskel erzeugte Kraft nach dem Grad der Aktivierung, schließlich kann man mit einem Skelettmuskel bewusst mehr oder weniger Kraft erzeugen, aber auch die maximal mögliche Kontraktionskraft variiert je nach Längenposition und Kontraktionsgeschwindigkeit. Obwohl Muskelkräfte durch invasive Methoden mittels Kraftsensoren, Arthroplastiksystemen (künstliche Gelenksysteme) oder Simulationen in Leichenmodellen gemessen werden können, gibt es derzeit keine nichtinvasiven experimentellen Methoden, mit denen die In-vivo-Kraft intakter Muskeln gemessen werden kann. Ausgehend von muskelphysiologischen Modellen der Kontraktion, auf welche an einem anderen Punkt eingegangen wird, und einfachen mechanischen Konzepten können demnach Muskelkräfte nur näherungsweise bestimmt bzw. verhältnismäßig angegeben werden.

Gelenkmechanik

Die Gelenkmechanik funktioniert also nach den Hebelgesetzen. Wie viel Kraft dabei ein Muskel auf ein Gelenk übertragen kann, hängt von der Länge des jeweiligen Hebelarms ab. Dieser ergibt sich aus dem senkrechten Abstand vom Muskel bzw. seiner Sehne (Wirkungskraftlinie) zum Drehzentrum. So ergeben sich für verschiedene Muskeln entsprechende Hebelarme, mit welchen sie auf Gelenke einwirken, die sie überziehen und im Falle einer Kontraktion zur Drehung bringen können.

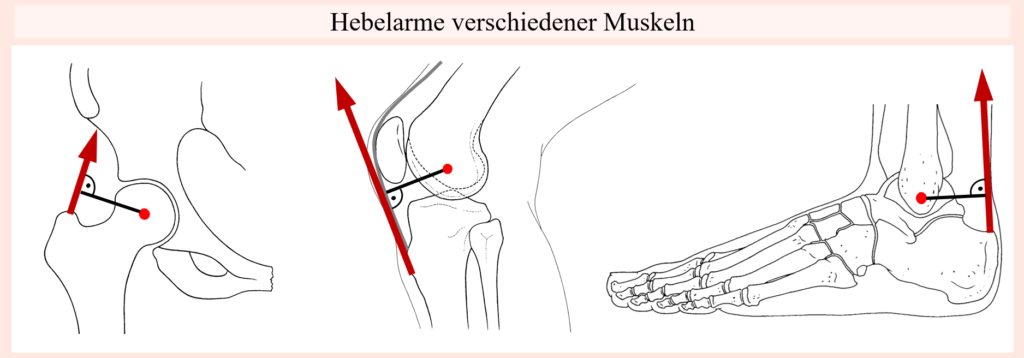
Bedenkt man, dass die Anatomie der Muskeln logischerweise erhalten bleibt, also sowohl Ursprung als auch Ansatzpunkt gleich bleiben, aber die Gelenkwinkelposition verändert werden kann, dann hat dies zur Folge, dass auch die Wirkungskraftlinie von Muskeln in Bezug auf den Drehpunkt je nach Gelenkwinkelposition variiert und damit ebenso der Hebelarm von Muskeln auf das Gelenk verändert wird. Das bedeutet, dass, selbst wenn die erzeugte Muskelkraft gleich bleiben würde, ein Muskel abhängig von der Gelenkwinkelposition ein unterschiedlich starkes Drehmoment an der Drehachse verursacht. Dies gilt wohlgemerkt für die meisten Skelettmuskeln, besonders anschauliche und einfache Beispiele sind dabei der Gluteus maximus und sein Hebelarm bei gestreckter im Vergleich zu gebeugter Hüfte, als auch der Biceps brachii (siehe Grafik) bei unterschiedlichen Flexionswinkeln des Ellbogens.

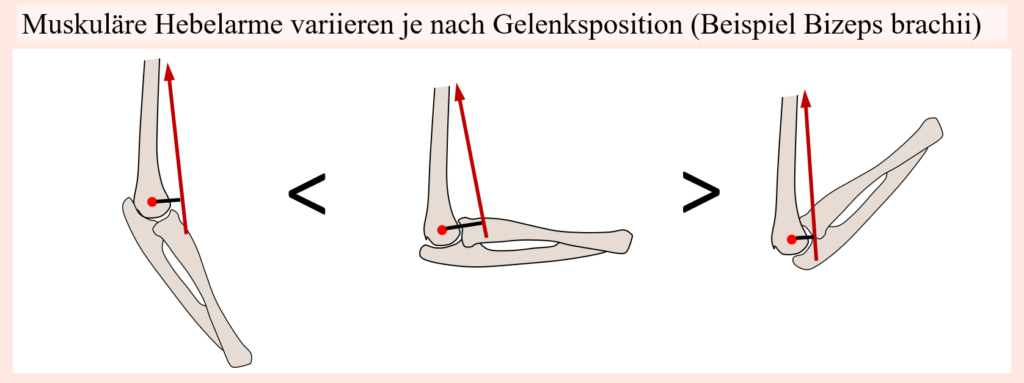
Die Muskelkraft ist wohlgemerkt nur eine der Kräfte, welche auf das Skelettsystem und die Gelenke einwirken. Die allgegenwärtigste dieser einwirkenden Kräfte ist die Schwerkraft, welche hier auf der Erde alle Körper Richtung Erdmittelpunkt zieht. Dadurch, dass die Schwerkraft unaufhörlich wirkt, sind wir dieser auch ununterbrochen ausgesetzt. So wirkt sowohl auf unseren Körper, samt all seinen Bestandteilen, deren Gewichtskraft, so wie auch auf allen anderen Körper. Im Sinne der Gelenkbelastung wirken natürlich auch diese Kräfte auf die Drehachsen unseres Körpers ein und können dabei translatorische Bewegungen sowie Drehbewegungen durch die Entstehung von Drehmomenten auslösen.

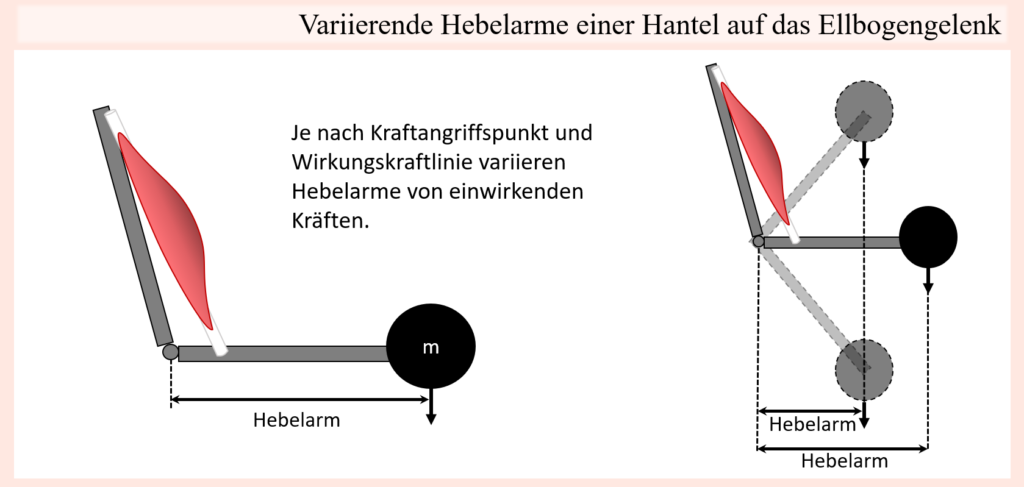
Das Prinzip hinter den Effekten, welche auf den Körper einwirkende Kräfte erzeugen, ist immer dasselbe, egal ob es um die Gewichtskraft der eigenen Gliedmaßen, um einen Gegenstand, den man in der Hand hält, die eigene Muskulatur, oder um ein Seil, an dem man zieht, geht. Insofern eine Kraft am Bewegungsapparat einwirkt, entscheidet deren Angriffspunkt, Wirkungslinie, Betrag, sowie eventuelle Muskelkräfte, welche dieser Kraft vielleicht entgegenwirken, über die mechanische Belastung der Gelenke und der daraus folgenden Bewegung.

Oftmals wird hierbei auch zwischen zwei Arten von Kräften unterschieden, einerseits die vom Bewegungsapparat erzeugte Muskelkraft und andererseits auf den Körper einwirkende Kräfte wie die Schwerkraft, welche als „Last“ bezeichnet werden. Des Weiteren wird dann auch oft zwischen „Lastarm“, als Hebelarm, einer Last in Bezug auf eine Drehachse, und „Kraftarm“, als Hebelarm eines der Last gegenübergestellten Muskels unterschieden. Diese unterschiedliche Bezeichnung war eigentlich gedacht, um mehr Ordnung in die Sache zu bringen, führt aber vereinzelt dazu, dass geglaubt wird, es handle sich hierbei um verschiedene Größen. Dem ist wohlgemerkt nicht so, vielmehr handelt es sich dabei immer schlicht um eine Kraft und einen Hebelarm, die Bezeichnung „Lastarm“ oder „Kraftarm“ sind keine eigentlichen physikalischen Größen, sondern sollen nur aufzeigen, welcher Kraft entsprechender Hebelarm zuzuschreiben ist.

statisches Gleichgewicht

Die von der Skelettmuskulatur erzeugte Kraft dient vor allem dazu, anderen Kräften, wie der Schwerkraft entgegenzuwirken. Zieht also zum Beispiel die Gewichtskraft des Unterarms und der Hand diese nach unten (durch ein erzeugtes Drehmoment, welches den Ellbogen zur Extension verleitet), dann kann die ellbogenbeugende Muskulatur wie der Bizeps hier durch ihre Kontraktion ein entgegengesetztes Drehmoment erzeugen. Nach dem 2. Newtonschen Gesetz wissen wir, dass die Änderung des Bewegungszustandes gleich der Summe aller einwirkenden Kräfte ist. Um die obige Terminologie zu nutzen, ergibt sich in diesem Falle die wirkende Kraft also durch das Produkt aus Muskelkraft*Kraftarm bzw. Last*Lastarm. Wenn Last*Lastarm = Kraft*Kraftarm, also beide Drehmomente identisch sind, befindet sich das Gelenk in Ruhestellung, weil die Summe der Kräfte, bzw. Drehmomente gleich 0 ist. Gleiches ist auch der Fall, wenn gegensätzliche Muskeln kontrahieren und ein gleich hohes Drehmoment erzeugen. Wenn z.B. das vom Trizeps erzeugte Drehmoment, welches den Ellbogen zur Streckung verleitet, und das vom Bizeps erzeugte Drehmoment, welches den Ellbogen zur Beugung verleitet, identisch sind und keine weiteren relevanten Kräfte einwirken, dann bleibt das Gelenk in Ruhe.

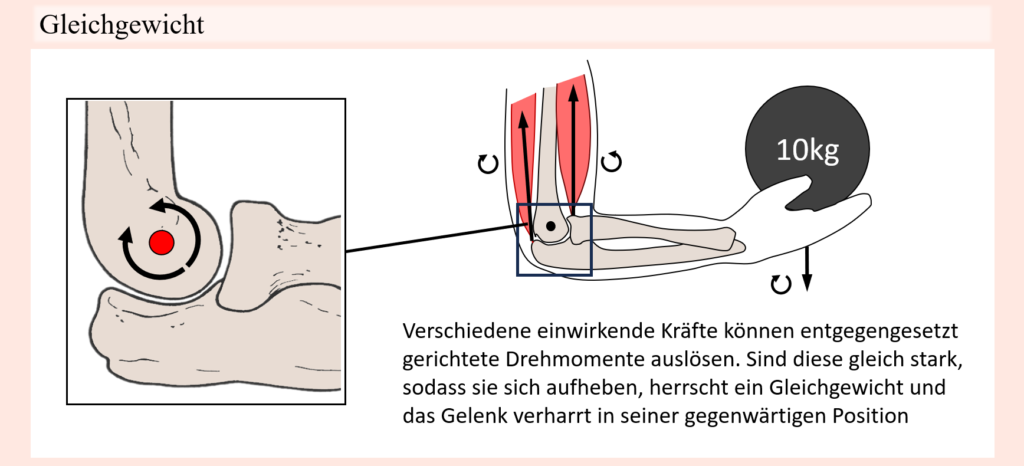
Was das Gleichgewicht angeht, gilt also der Satz: „Ein Körper befindet sich im statischen Gleichgewicht, wenn er keine beschleunigte geradlinige Bewegung (Translation) und keine beschleunigte Drehbewegung (Rotation) erfährt“. Nach der heutigen Definition des physikalischen Kraftbegriffes ist dies auch logisch, denn wenn die Addition aller einwirkenden Kräfte nicht 0 ergäbe, würde in der Summe eine Kraft auf den Körper wirken und der Körper würde sich unter dem Einfluss dieser Kraft beschleunigt fortbewegen, ergo wäre er dann nicht im statischen Gleichgewicht. Das analoge Argument gilt für die Summe der Drehmomente. Wenn die Summe aller einwirkenden Drehmomente nicht 0 ergäbe, so würde noch ein Drehmoment auf den Körper wirken und der Körper würde sich beschleunigt drehen und wäre folglich ebenfalls nicht im statischen Gleichgewicht.

Aus biomechanischer Sicht sind Kräftegleichgewichte vor allem deswegen so wichtig, weil hierdurch unbekannte Variablen berechnet werden können. Denn selbst wenn die Muskelkraft selbst nicht bekannt ist, so ist im statischen Gleichgewicht, also wenn keine beschleunigte Drehbewegung stattfindet, die Summe aller Drehmomente gleich null. Möchte man so zum Beispiel die Muskelkraft des Bizepses berechnen in einer Position berechnen, wo der Ellbogen in gebeugter Stellung, samt einer 10 kg Hantel in der Hand gehalten wird, dann geht dies ganz einfach, wenn wir einige Faktoren idealisieren.

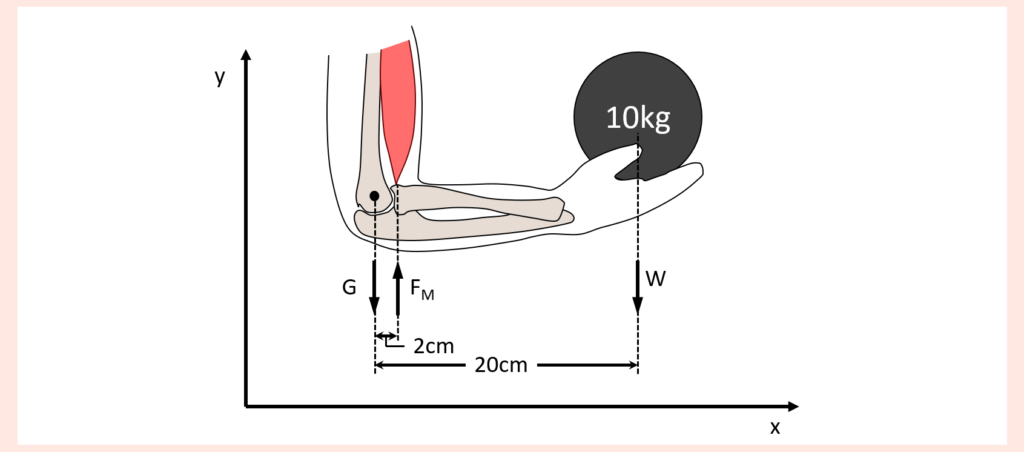
Das Ellenbogengelenk ist 90° gebeugt, die auf der Hand gehaltene Masse von 10 kg übt eine Gewichtskraft von rund 100 N (W für Widerstand) senkrecht nach unten aus. Zur Erhaltung des Gleichgewichts wird der Bizeps angespannt und erzeugt eine entgegengesetzte Kraft nach oben (F_M). Bezogen auf das XY-Koordinatensystem verlaufen Gewichtskraft und Muskelkraft in diesem vereinfachten Modell parallel zur y-Achse. Für die Hebelarme der Last und des Bizeps werden gerundete Werte von 20 cm und 2 cm angenommen. Die Muskelkraft F_M ist hingegen unbekannt. Aus dem Kräftegleichgewicht folgt nun aber:

-F_M*2 cm + 100 N * 20 cm = 0 Ncm

Daraus ergibt sich, dass die Kraft des Bizeps 1000 N beträgt, denn im Gleichgewicht müssen sich die nach unten gerichtete Kraft und die nach oben gerichtete Kraft aufheben.

Gelenkbelastung

Als Belastung eines Gelenks bezeichnet man die Kraft, die zwischen den knöchernen Gelenkpartnern wirkt. Kenntnis über das Ausmaß jener Belastung der Gelenke ist von großer praktischer Wichtigkeit, wenn es um das Vorgehen bei der Rehabilitation, um die Entwicklung künstlicher Gelenkersatze und natürlich die Erforschung der Ursachen von Erkrankungen geht. In Einzelfällen ist es wie gesagt möglich zum Beispiel mittels Leichenpräparaten z.B. mithilfe eines instrumentierten, künstlichen Gelenkersatzes Gelenkbelastungen direkt zu messen, meist ist man jedoch auf biomechanische Modellrechnungen angewiesen. Solch ein „Modell“ entspricht dabei definitionsgemäß einer gewissen Simplifizierung, weswegen entsprechende Rechnungen auch Annahmen, bzw. Annäherungen entsprechen.

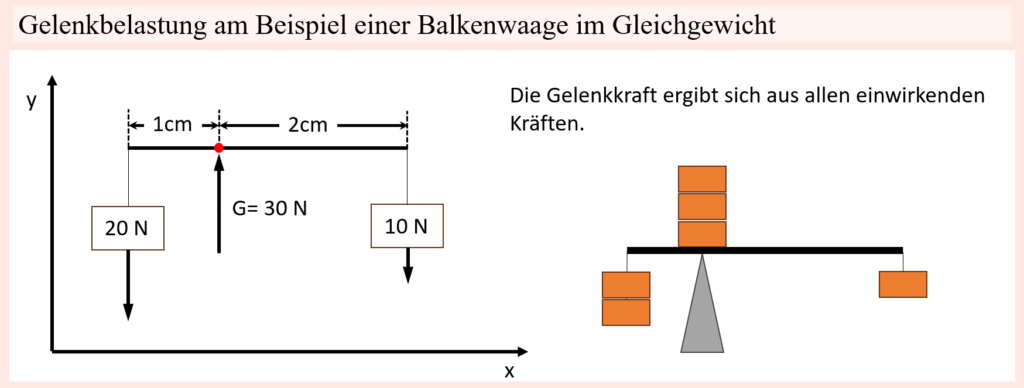
Um die Gelenkbelastung zu ermitteln, werden lediglich alle Kräfte zusammengefasst, die auf das Gelenk wirken. Das Prinzip dahinter wird durch eine Balkenwaage deutlich.

Im obigen Beispiel, beim Kräftegleichgleichgewicht des gebeugten Armes haben wir also in diesem Sinne zwei Kräfte, welche einmal in die +y Richtung und einmal in die -y Richtung laufen. Dadurch, dass es sich um ein Kräftegleichgewicht handelt, folgt, dass Muskelkraft + Last + Gelenkkraft = 0 ergeben und weil wir die Werte für die Muskelkraft und Last wissen, ergibt sich auch die Gelenkbelastung:

G + 1000 N – 100 N = 0 N

G = -900 N

Die Gelenkkraft (G) hat den Betrag 900 N. Ihr negatives Vorzeichen bedeutet, dass die Gelenkkraft G in negative y-Richtung weist. Mit anderen Worten, der Humerus wird mit einer Kraft von 900 N gegen die Ulna gedrückt. Man erkennt ebenso, dass die Muskelkraft des Bizeps den größten Anteil zur Gelenkkraft beiträgt.

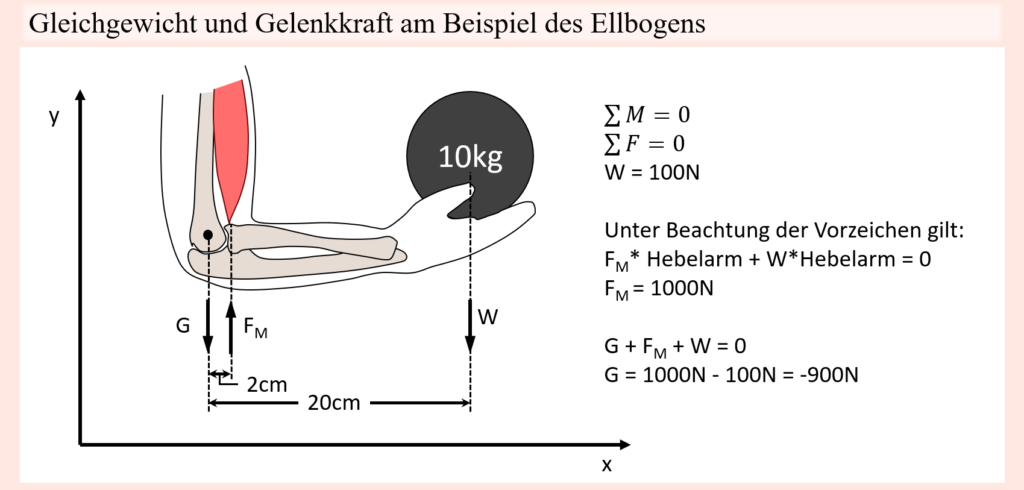
In diesem Beispiel wurde wohlgemerkt lediglich der Bizeps als muskuläre Komponente miteinbezogen. In Realität sind neben Agonisten aber auch immer zu einem gewissen Teil Antagonisten einer Bewegung beteiligt. Wenn also in dieses Beispiel noch der Trizeps mit einberechnet wird, dann entspricht dies einer weiteren in +y Richtung verlaufenden Kraft.

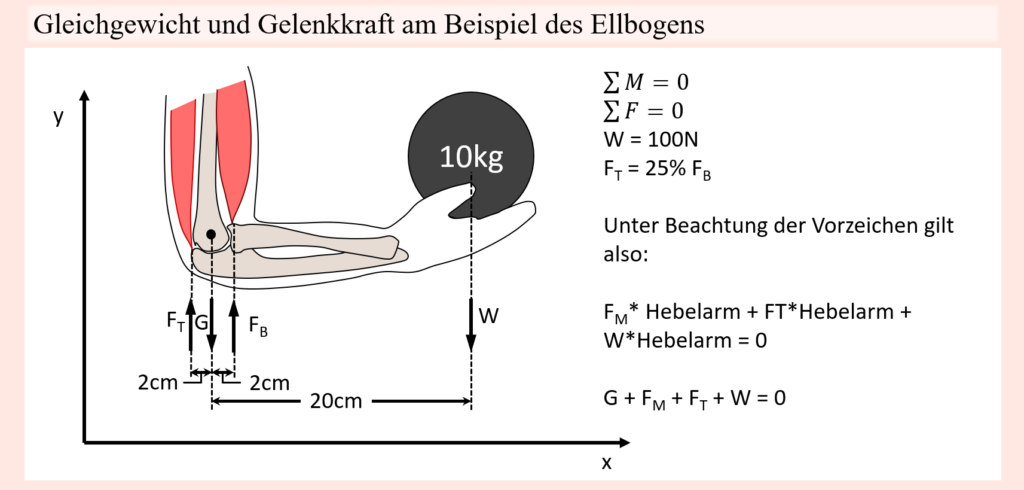
Nehmen wir, für dieses Beispiel nun an, die Kraft des Trizeps entspräche 25 % der Kraft des Bizeps, also 0,25F_B (Anhand der gegebenen Werte muss solch eine zusätzliche Annahme erfolgen, weil man die zwei Variablen ansonsten nicht auflösen kann), dann folgt im Kräftegleichgewicht (unter Beachtung der Vorzeichen):

-F_B*2 cm + 100 * 20 cm + 0,25F_B*2cm = 0 Ncm

Die vom Bizeps erzeugte Kraft beträgt damit 1333,3 N und die Kraft des Trizeps 333,3 N und für die Gelenkskraft (G) folgt:

G + 1333 N + 333 N – 100 N = 0 N

G = -1566 N

Durch die Inbezugnahme des Trizeps steigt also sowohl die Gelenkbelastung als auch die Kraft, welche der Bizeps aufbringen muss, was ja auch logisch ist, schließlich muss der Bizeps nicht nur der externen Last, sondern noch dazu dem Trizeps entgegenwirken. In bestimmten Situationen ist eine erhöhte Antagonistenaktivität durchaus vorteilhaft, weil durch die erhöhte Gelenkbelastung die Unempfindlichkeit der Haltung gegenüber äußeren Störungen erhöht wird, mit anderen Worten das Gelenk stabilisiert wird. Muss jedoch ein Muskel gegen starken Widerstand eines Antagonisten eine Haltung oder Bewegung erzwingen, so können sehr hohe Gelenkbelastungen resultieren.

Andere klassische Beispiele für die Veranschaulichung von der Gelenkbelastung sind die Belastung des Hüftgelenks beim Einbeinstand, sowie das Femoropatellargelenk bei Kontraktion des Quadrizeps und unterschiedlichem Kniewinkel. Letzteres beschreibt die Kniescheibe (Patella) und die Kraft, mit der diese und der Oberschenkel zusammengedrückt werden. Als Sesambein ist die Patella in der Quadrizeps- bzw. Patellasehne eingebettet. Hier fungiert sie als Abstandhalter für die Sehne zum Drehzentrum des Kniegelenkes, wodurch der Hebelarm des Quadrizeps vergrößert wird. Durch den Zug des Quadrizeps und der Quadrizepssehne auf der einen und dem Gegenhalt der Patellasehne, welche am Schienbein befestigt ist, auf der anderen Seite entsteht eine Gelenkresultierende welche durch das Drehzentrum des Femoropatellargelenkes verläuft. Das Ausmaß hiervon ist ein Maß für die auf das Gelenk einwirkenden Kräfte und lässt sich gut durch die geometrische Addition der Vektoren im Kräfteparallelogramm darstellen. Durch vermehrte Anspannung des Quadrizeps bei Kniebeugung sowie den kleineren Winkel β ist die Resultierende in Beugestellung größer als in Streckstellung, d. h. mit zunehmender Beugung und vermehrter Anspannung des Quadrizeps vergrößert sich die Gelenkbelastung im Femoropatellargelenk. Im Kräftegleichgewicht ist natürlich auch hier die Summe aus Muskelkraft, Patella-Kraft und Femoro-patellare Kraft = 0.

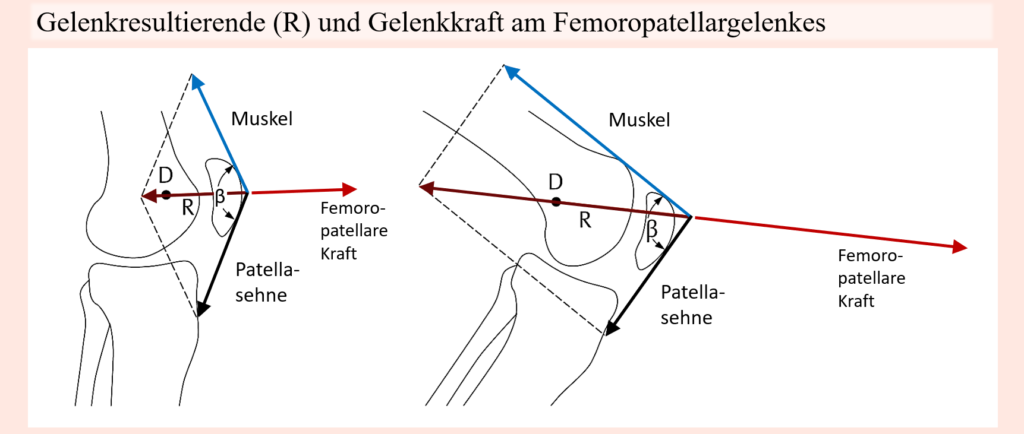
Im aufrechten Stand auf beiden Beinen wird die Last des Oberkörpers gleichmäßig auf beide Hüftgelenke und zudem sind im Vergleich zum Einbeinstand weniger Muskelkräfte zum Stabilisieren nötig.

Beim Einbeinstand oder während des Gehens in der Standbeinphase verlagert sich der Teilkörperschwerpunkt (S) wegen des angehobenen Beines aber auf die gegenüberliegende Seite des Standbeines, sodass das Teilkörpergewicht (K) deutlich medial des Hüftgelenks wirkt. Hieraus resultiert ein Drehmoment der Last, welches dazu tendiert, das Becken, bzw. den Körperteil oberhalb des Gelenks zur Seite des angehobenen Beines hin abzukippen. Damit dies nicht passiert, darf in Summe kein Drehmoment entstehen, wofür die Muskulatur sorgt, indem sie der Gewichtskraft entgegenwirkt (indem ein gegensätzliches Drehmoment erzeugt wird). In diesem Falle liefert diese Kraft vor allem die Muskelkraft (M) der Hüftabduktoren (Gluteus medius/minimus). Im Vergleich zur Kraft des Teilkörpergewichts greift diese Muskelkraft aber mit einem etwa dreimal kürzeren Hebelarm am Hüftgelenk an, das bedeutet der Hebelarm der Muskelkraft und der Hebelarm des Teilkörpergewichts stehen im Verhältnis von etwa 1:3. Zur Stabilisierung der Hüfte muss die Muskelkraft demnach so hoch ausfallen (in diesem Fall etwa das Dreifache), dass die Resultierende durch das Hüftgelenk verläuft. Die auftretende Gelenkbelastung ergibt sich dann wiederum aus der Summe aus Muskelkraft und Last.

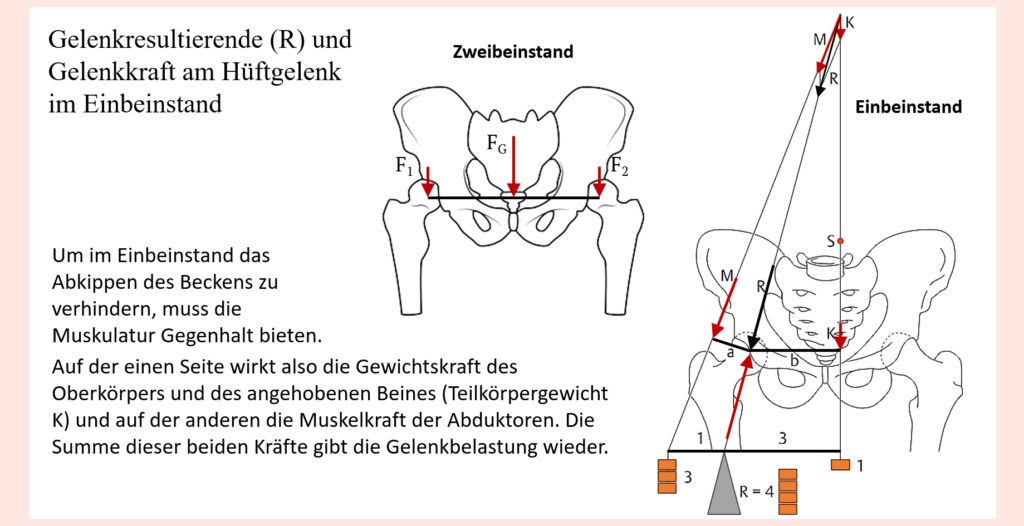
Im Gegensatz zur reinen Belastung eines Gelenkes, welche lediglich alle einwirkenden Kräfte zusammenfasst, wird bei der Gelenkbeanspruchung die funktionelle Kontaktfläche miteinbezogen. Das bedeutet, mechanisch gesehen entspricht die Beanspruchung dem Druck.

Druck beschreibt, wie eine Kraft von einem Körper durch eine Grenzfläche auf einen anderen Körper übertragen wird und ist definiert als senkrecht durch eine Fläche hindurchtretende Kraft, geteilt durch die Fläche, also kurz Kraft pro Fläche (N/m²). Je größer die kraftaufnehmende Fläche, desto besser verteilt sich die einwirkende Kraft und umso geringer ist der Gelenkdruck bzw. Gelenkbeanspruchung und umso höher der Druck, je kleiner die Fläche.

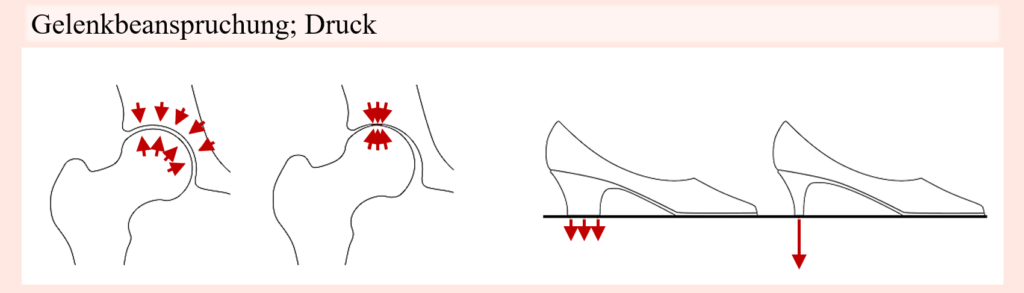
Beispiel einer mechanischen Analyse anhand zwei einzelner Muskeln

Im Folgenden werden wir anhand zwei einzelner Beispiele einige wesentliche der oben dargestellten biomechanischen Prinzipien einsetzen, um die wirkenden Kräfte am Schultergelenk zu identifizieren. Dabei beschränken wir uns auf eine zweidimensionale Analyse mit nur einem Muskel. Ebenso wird das Modell idealisiert, sprich es wird angenommen, dass kein Gewebe sich verformt, keine Reibung im System vorhanden ist und keine Beschleunigung stattfindet. Hierbei knüpfen wir an die weiter oben bereits aufgegriffene Gegenüberstellung des seitlichen Deltoids und des Supraspinatus an. Im entsprechenden obigen Abschnitt wurde hierbei lediglich aufgezeigt, dass jene beiden Muskeln frontal betrachtet ähnlich große Hebelarme in Bezug auf das Schultergelenk besitzen. Bei einer etwas genaueren Auseinandersetzung wird man aber durchaus gewisse Unterschiede feststellen können.

Beginnen wir also mit dem Supraspinatus. Zur besseren Veranschaulichung erstellen wir hierzu ein Freikörper-Diagramm, wobei wir den Körper, um den es geht, isolieren und mittels Pfeilen alle relevanten wirkenden Kräfte einzeichnen. Der Körper, um den es in diesem Fall geht, ist der Oberarmknochen, bzw. Oberarmkopf, wobei das Schulterblatt der Übersichtlichkeit halber ebenso eingezeichnet ist. Wie gesagt wird angenommen, dass keine Beschleunigung gegeben ist, das heißt wir haben es mit einem Kräftegleichgewicht zu tun. Das wiederum können wir nutzen, um unbekannte Variablen aufzulösen, indem wir zuallererst die am Drehzentrum wirkenden Kräfte gleich 0 setzten. Damit die Schulter statisch gehalten wird, erzeugt der Supraspinatus in diesem Modell genau so viel Kraft F_S, um die Wirkung der Last F_G aufzuheben. Ebenso können wir die resultierende Gelenkkraft F_R in x und y Richtung berechnen, indem wir auch die Summe, der in x und y wirkenden Kräfte gleich 0 setzen, denn auch hier müssen sich die einwirkenden Kräfte und die Gelenkkräfte auflösen, damit das Gleichgewicht möglich ist. In diesem Beispiel beläuft sich der Betrag der Supraspinatuskraft also auf 725 N und die Gelenkreaktionskraft beträgt gemäß Newtons 3. Gesetz nach lateral 203 N und nach superior 100 N.

Die gleiche Berechnung kann nun auch mit dem seitlichen Deltamuskel an Stelle des Supraspinatus gemacht werden. Dabei beläuft sich der Betrag der Muskelkraft auf etwa 694 N und die Gelenkreaktionskraft beträgt nach lateral rund, 531 N und nach superior rund 345,8 N. Weil die Hebelarme der Muskeln vergleichbar sind, ist auch die benötigte Muskelkraft, um der Last entgegenzuwirken und ein Kräftegleichgewicht zu erreichen, ähnlich (Supraspinatus, 725 N vs. Deltamuskel, 694 N), jedoch erzeugt der Deltamuskel im Vergleich eine deutlich höhere Kraft nach superior und der Supraspinatus eine höhere Kraft nach medial.

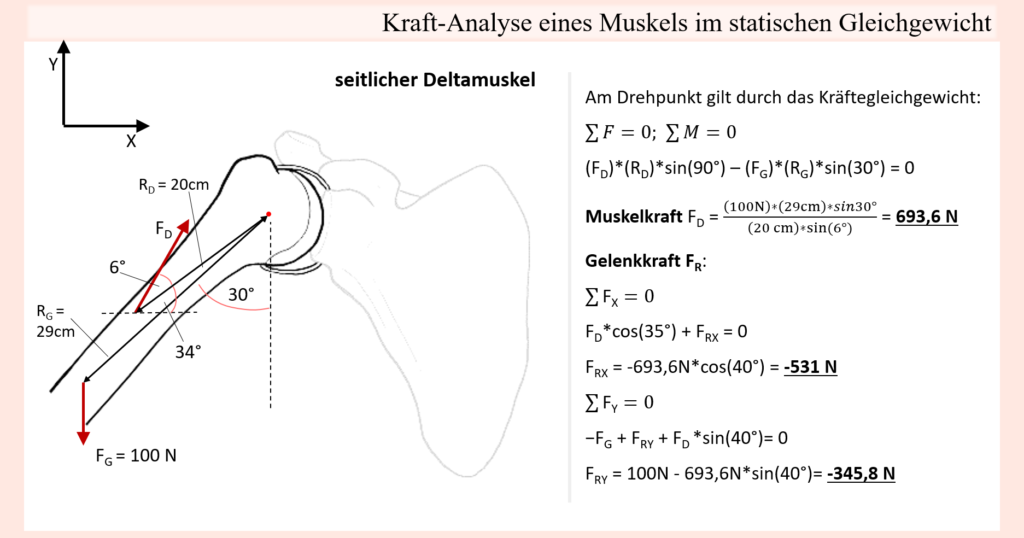
Befindet sich ein System im statischen Gleichgewicht, gibt es keine äußeren Kräfte, da es keine Beschleunigung gibt, und die Summe der äußeren Kräfte gleich null gesetzt werden kann. Wenn ein Objekt jedoch beschleunigt wird, dann bedarf es einer Kraft, welche die Trägheit überwindet, und eine Bewegungsänderung hervorruft (Beschleunigung), weswegen die Summe der Kräfte nicht mehr gleich 0 ist. Um dies zu verdeutlichen, können wir auch wieder ein einfaches Modell betrachten.

Nehmen wir an, man hebt einen Körper mit einer Masse von 15 kg senkrecht nach oben. Hält man den Körper einfach nur statisch in der Luft, dann herrscht ein Kräftegleichgewicht, was bedeutet, dass die Gewichtskraft des Körpers und die entgegengerichtete Kraft nach oben sich gegenseitig aufheben, sodass der Körper in jener Position verharrt. Mit anderen Worten, um den Körper so zu halten muss eine der Schwerkraft entgegengesetzte Kraft ausgeübt werden, welche gleich groß ist, wie die Gewichtskraft des Körpers. Die Gewichtskraft ergibt sich aus der Masse des Körpers, also 15 kg und der Erdbeschleunigung von 9,81 m/s². Insofern eine Abweichung von 2 % vernachlässigbar ist, was bei einfachen mechanischen, bzw. biomechanischen Berechnung meist Fall ist, kann man die Erdbeschleunigung auch auf 10 m/s² aufrunden. Der Körper wird also mit rund 10 m/s² senkrecht nach unten beschleunigt, wobei auf ihn eine Gewichtskraft von 15 kg * 10 m/s² = 150 N wirkt. Um den Körper also statisch in der Luft zu halten, braucht es eine entgegengesetzte Kraft von 150 N. Und auch wenn es genau genommen nicht ganz akkurat ist, kann man auch bei langsamen Bewegungen statische Gleichgewichtsbedingungen anwenden, weil die geringe Beschleunigung hierbei vernachlässigt werden kann. Wenn der Körper aber mit einer höheren Beschleunigung von sagen wir 5 m/s² angehoben wird, dann ist die Summe der Kräfte nicht gleich 0, sondern entspricht dem Produkt aus der Masse des Körpers und der entsprechenden Beschleunigung, also in diesem Fall 15 kg * 5 m/s². Diese Kraft muss der Kraft addiert werden, welche benötigt wird, um der Schwerkraft entgegenzuwirken (Masse*Erdbeschleunigung), wodurch sich eine erforderliche Gesamtkraft von 225 N ergibt, um den Körper entgegen der Schwerkraft mit 5 m/s² nach oben zu beschleunigen.

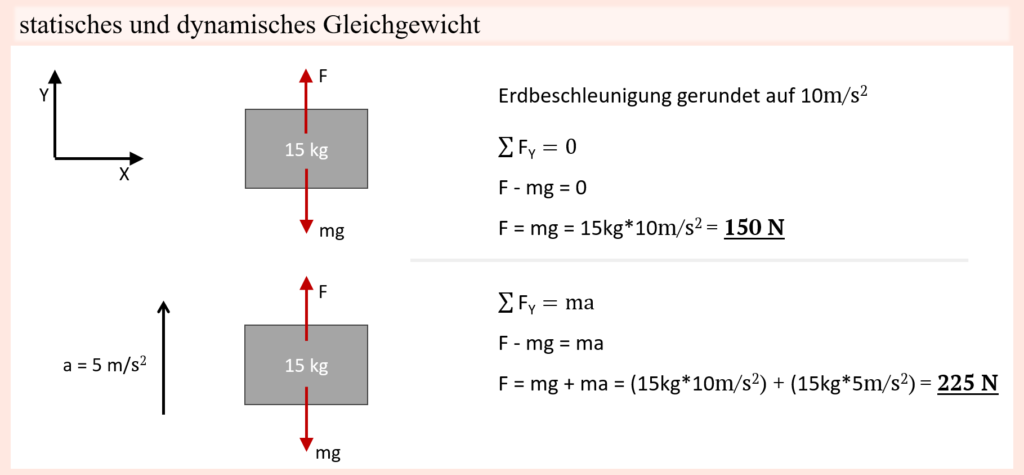
Für Rotationsbewegungen gilt eine analoge Beziehung nur eben in Bezug auf das Trägheitsmoment und der Winkelbeschleunigung. Denn genauso wie die Masse ein Maß für den Widerstand gegen lineare Beschleunigung ist, ist das Trägheitsmoment ein Maß für den Widerstand gegen Winkelbeschleunigung. Es gilt also auch hier, dass die Summe der Drehmomente proportional zum Trägheitsmoment und zur Winkelbeschleunigung (α) dieses Körpers ist, wobei das Trägheitsmoment größer ist, je weiter die Massenpunkte vom Drehzentrum entfernt sind. Beispielsweise reduziert eine Eiskunstläuferin so bei einer Pirouette ihr Trägheitsmoment, indem sie ihre Arme nahe an den Körper bringt, wodurch ihre Winkelbeschleunigung zunimmt.

3. Gesetz von Newton; actio – reactio

Also gut, einwirkende Kräfte sorgen also für Bewegungsänderungen, mit anderen Worten Kräfte entsprechen äußeren Einflüssen. Doch woher kommen diese Einflüsse?

Unsere unmittelbare Erfahrung zeigt, wie auch schon von Aristoteles dargelegt, dass Kräfte auf einen Körper von anderen Körpern ausgehen. Zwei Körper können sich also gegenseitig beeinflussen (der Beweger und der Bewegte). Das kann zum einen durch direkte Berührung erfolgen, was natürlich die offensichtlichste Möglichkeit ist und lange Zeit auch als die einzige Möglichkeit verstanden wurde. Dies zeigt sich daran, dass vor Newton die Gravitationskraft, sei es im Falle der Himmelskörper, welche sich auf Kreisbahnen bewegen oder aber der Stein, der wie von allein Richtung Boden fällt, nicht mit „erzwungenen“ Bewegungen gleichgestellt wurde (bzw. man nicht daran dachte es zu versuchen). Sogar der offensichtliche Einfluss, den die Sonne auf die sie umkreisenden Planeten ausübt, hat man sich durch so einen direkten Einfluss versucht zu erklären, vermittelt durch eine Art von Medium, auch „Äther“ genannt. Erst Newton verzichtete auf diesen Äther und formulierte sein Gravitationsgesetz als unmittelbare Fernwirkung zwischen den Himmelskörpern. Wie diese Fernwirkung über den leeren Raum aber funktioniert, das wusste Newton nicht und wurde erst von Einstein mit seiner allgemeinen Relativitätstheorie entschlüsselt, nämlich durch die Krümmung von Raum und Zeit.

Aber unabhängig von der genauen Art und Weise der Beeinflussung gehören zu einer Kraft immer zwei, ein Körper, auf den die Kraft wirkt, und ein Körper, von dem die Kraftwirkung ausgeht. Newton erkannte aber noch etwas Entscheidendes, nämlich Wechselwirkungskräfte, welche er in seinem dritten Bewegungsgesetz etwa folgendermaßen formulierte:

Zwei Körper üben aufeinander betragsmäßig gleiche, aber entgegengesetzt gerichtete Kräfte aus (actio gleich reactio). Übt A eine Kraft auf B aus, so übt B eine gleich große, entgegengesetzt gerichtete Kraft auf A aus.

Auch wenn es so aussieht, als gehe allein von einem der Körper eine Kraftwirkung aus (actio), so ist diese Kraft doch immer begleitet von einer Kraft, die der andere Körper ausübt (reactio). Historisch werden jene beiden Kräfte oft als Aktionskraft (actio) und Reaktionskraft (reactio), oder einfach Kraft und Reaktionskraft bezeichnet. Doch dies könnte zu Missverständnissen verleiten, weil es impliziert, dass die eine der beiden Kräfte die Ursache der anderen ist oder der anderen vorausgeht. In Wahrheit treten aber immer beide gleichzeitig auf, das heißt keine geht der anderen voraus. Vielmehr ist keine ohne die andere denkbar, wie etwa, um eine Metapher zu nutzen, zwei Seiten derselben Medaille. Aus diesem Grund ist wohl die Bezeichnung „Wechselwirkungskräfte“ besser geeignet. Jede Wirkung von einem Körper auf einen anderen Körper ist also mit einer entgegengesetzten Wirkung verknüpft. Besonders anschaulich ist das zum Beispiel beim Ziehen an einem Gummiband, wobei das Gummiband zurückzieht. Das knüpft natürlich auch an der weiter obig getätigten Aussage an, dass Kraft keine Eigenschaft eines Körpers ist, eben weil ein einzelner Körper aus sich heraus weder eine Kraft ausüben noch eine Kraftwirkung erfahren kann. Wohlgemerkt ist es nicht gerade verwunderlich, dass vor Newton, bzw. zu Zeiten vor Galilei dieses Wechselwirkungsprinzip nicht erkannt wurde, weil es oftmals so erscheint, als ob viele Kräfte einzeln auftreten würden. So wird ein massereicher Körper offensichtlich von der Masse der Erde angezogen, wie der Stein, der zu Boden fällt. Wo ist denn hier die zugehörige Gegenkraft? Tatsächlich wird auch die Erde im genau selben Maße vom Stein angezogen, wie der Stein von der Erde. Wenn man den Stein also in die Luft wirft, so wird nicht nur der Stein wieder herunterfallen, sondern auch die gesamte Erde wird spiegelbildlich eine entsprechende Gegenbewegung ausführen, nur mit sehr viel geringerer Beschleunigung, da sie eine viel größere Massenträgheit als der Stein besitzt. Die Bewegung der Erde ist deswegen also gegenüber der Bewegung des Steins nicht wahrnehmbar, aber sie existiert. Hier wird ersichtlich, dass das dritte Newtonsche Gesetz eben nicht besagt, dass zwei wechselwirkende Körper im gleichen Maße beschleunigt werden. Dies kann man sich auch mit einem anschaulicheren Beispiel verständlich machen. Man stelle sich vor, zwei Personen mit der gleichen Masse stehen je auf einem Skateboard und sind mit einem Seil, welches sie in den Händen halten, verbunden. Wenn man darüber hinaus annimmt, dass sie auf einer ebenen, horizontalen Fläche stehen und die Skateboards, auf denen sie stehen, dieselben Eigenschaften aufweisen, dann werden sich beide in die Richtung des jeweils anderen bewegen, egal, wer am Seil zieht. Auf beide wirkt dieselbe Kraft und durch ihre gleiche Masse folgt, dass sie auch gleich stark beschleunigen. Wenn nun aber eine Person eine bedeutend größere Masse aufweist, dann wird zwar immer noch dieselbe Kraft auf beide einwirken, diese wird bei der massereicheren Person aber eine geringere Beschleunigung hervorrufen.

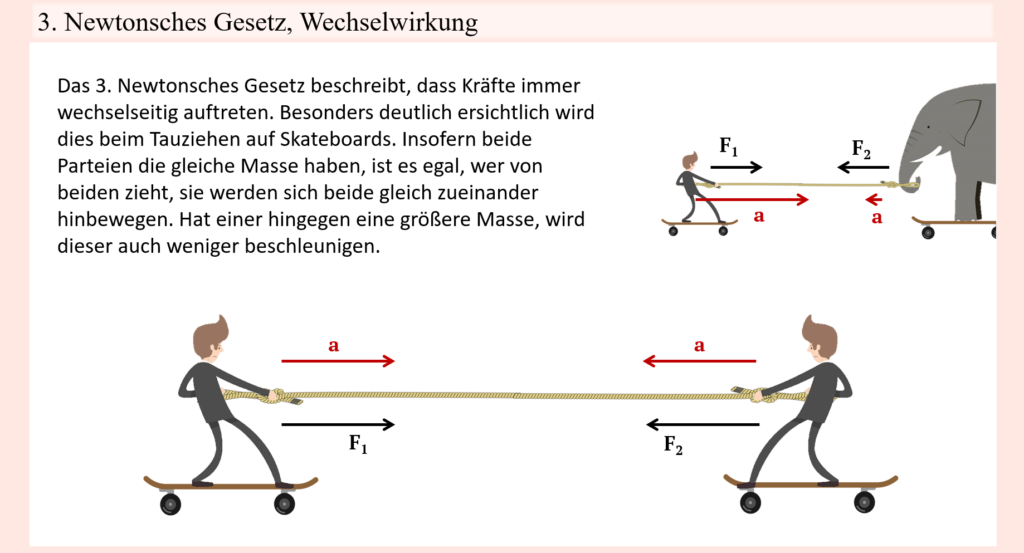
Wenn man genauer darüber nachdenkt, wird ersichtlich, wie allgegenwärtig das 3. Gesetz von Newton tatsächlich ist.

Wie vorhin erwähnt, erzeugen wir durch das Gaspedal im Auto eine Antriebskraft nach vorne (wenn der Vorwärtsgang eingelegt ist), welche dafür sorgt, dass wir uns auch nach vorne bewegen. Na ja, das stimmt nicht ganz, bzw. wir haben einen wesentlichen Zwischenschritt übersprungen. Tatsächlich werden durch die Motorkraft die angetriebenen Räder so gedreht, dass sie eine Kraft nach hinten auf den Boden (Körper A) ausüben. Gleichzeitig mit ihr wirkt aber die Reaktionskraft auf den Reifen (Körper B) und ist entgegengesetzt, also nach vorn gerichtet. Diese Reaktionskraft drückt letztlich das Auto nach vorne. Das Gleiche gilt wie gesagt für alle Kräfte. Springt man in die Luft, so übt man durch seine Muskelkraft eine Kraft nach unten in den Boden aus, erst die Reaktionskraft nach oben sorgt dafür, dass man nach oben springt.

Ein Missverständnis, welches im Kontext dieser Wechselwirkungskräfte durchaus aufkommen kann, ist die Verwechslung mit dem obig angesprochenen Kräftegleichgewicht, welches auftritt, wenn die auf einen Körper einwirkenden Kräfte sich gegenseitig aufheben (zum Beispiel zwei gegensätzliche Kräfte mit gleichem Betrag). Dies ist wohlgemerkt bei Wechselwirkungskräften nicht der Fall, weil diese je auf verschiedene Körper einwirken, ein Kräftegleichgewicht aber nur entsteht, wenn alle Kräfte, die auf ein und demselben Körper einwirken, sich aufheben, sodass F = 0.

Drehbewegungen

Nun gut, damit hätten wir die drei Newtonschen Gesetze und zugleich auch die Grundlage der klassischen Mechanik, nämlich die kausale Verbindung von Kräften und Bewegungen, samt der eigentlichen Bedeutung des Kraftbegriffs geklärt. Doch wenn man sich etwas weiter damit beschäftigt, wird man schnell merken, dass dies allein noch nicht ausreicht. Man stelle sich zum Beispiel einen Schraubenschlüssel vor, den man dazu benutz, eine festgezogene Mutter zu lockern. Dazu setzt man den Schraubenschlüssel auf den Kopf der Mutter und übt eine Kraft in die Drehrichtung aus. Genau hier wird man nun aber etwas Wesentliches feststellen, wenn man einmal die Kraft am Beginn des Schraubenschlüssel-Griffs, also nahe am Kopf ausübt und einmal dieselbe Kraft am hinteren Teil des Griffs. Trotz des gleichen Betrags der Kraft, welche auf den Schraubenschlüssel ausgeübt wird, fällt das Lockern der Schraube mit letzterer Methode bedeutend einfacher. Offenbar hängt die Bewegung des Schraubenschlüssels, bzw. der festgezogenen Mutter nicht nur von der Richtung und dem Betrag der Kraft, sondern auch von ihrem Angriffspunkt ab. Genauer gesagt, sie hängt nicht nur von der Größe der Kraft ab, sondern auch vom Abstand ihres Drehpunkts von der Wirkungslinie der Kraft. Und dies können wir sogar mathematisch ausdrücken, indem wir sagen, dass die gleiche Wirkung erfolgt, wenn das Produkt von Kraft F und besagtem Abstand den gleichen Wert hat. Somit spielt hier eine neue Größe eine Rolle, die als Drehmoment (M) bezeichnet wird, das Produkt aus dem Abstand (allgemein als „Hebelarm“ bezeichnet) und der Kraft F ist und somit die Einheit Nm (Newtonmeter) hat.

Im Vergleich zu den Bewegungsbeispielen und behandelten Sachverhalten bis zu diesem Punkt fällt hier etwas Entscheidendes auf, nämlich war bis zu diesem Punkt nie die Rede von Drehungen, sondern lediglich Bewegungen, in denen sich alle Punkte eines Körpers gleich im Raum bewegen. Hierbei spricht man von sogenannten Translationsbewegungen. Zu den Translationsbewegungen kommen aber auch Dreh- bzw. Rotationsbewegungen hinzu, wobei unterschiedliche Punkte eines Körpers unterschiedliche Wegstrecken zurücklegen. Aus diesen beiden Bewegungsformen setzt sich die Bewegung eines starren Körpers zusammen. Die besprochenen Bewegungsgesetze gelten aber wohlgemerkt für beide, nur dass gemäß der Tabelle unten charakteristische Größen der Translation mit analogen Größen der Drehbewegung ersetzt werden. Das heißt für jede Größe der linearen Bewegung gibt es eine korrespondierende Größe der Drehbewegung, wobei die Gleichungen für beide Bewegungsformen formal gleich sind. So beschreibt die Winkelgeschwindigkeit nichts anderes als die Winkeländerung pro Zeit, genauso wie die Geschwindigkeit die Ortsverschiebung pro Zeit beschreibt.

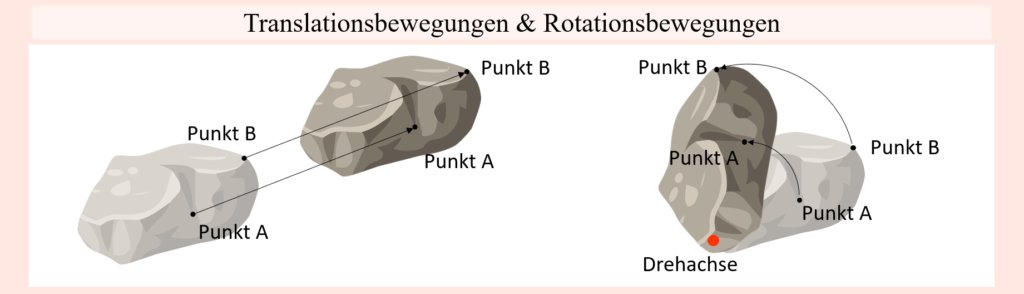
Translationsbewegung	Drehbewegung (Rotationsbewegung)
Ort (bzw. Weg, Verschiebung)	Drehwinkel
Masse	Trägheitsmoment
Geschwindigkeit	Winkelgeschwindigkeit
Beschleunigung	Winkelbeschleunigung
Kraft	Drehmoment

Ein wesentlicher Unterschied zu translatorischen Bewegungen ist der, dass jede Drehbewegung immer eine beschleunigte Bewegung ist, auch wenn der Betrag der Geschwindigkeit gleich bleibt, weil sich die Richtung ständig ändert. Aber bis auf das bleibt das Prinzip im Wesentlichen dasselbe. Um die Winkelgeschwindigkeit zu ändern, wird eine Winkelbeschleunigung benötigt, welche auch hier die zeitliche Änderung der Winkelgeschwindigkeit wiedergibt. Wohingegen die Masse Änderungen der Bewegung bei einer Translation entgegenwirkt (Trägheit), wirkt das Trägheitsmoment genauso Änderungen der Rotationsbewegung entgegen. Masse (Trägheit) und Trägheitsmoment sind also analoge Größen. Damit ein rotierender Körper also eine Winkelbeschleunigung erfährt, muss eine Kraft einwirken. Diese Kraft ist das Drehmoment. Ähnlich wie das zweite Newtonsche Gesetz sagt, dass ein Körper seine Bewegung nur dann ändert, wenn eine Kraft wirkt, so gilt im Falle der Rotation, dass sich eine Rotationsbewegung nur dann ändert, wenn ein Drehmoment wirkt.

Das Drehmoment ist also die Kraft, welche einen Körper zu einer Drehung verleitet, und ist somit bei Drehbewegungen (Rotationsbewegungen) eine zweckmäßigere Größe als eine alleinige Kraft. So wie wir obig eine Kraft definiert haben als die Ursache für eine Bewegungsänderung, also Beschleunigung, können wir das Drehmoment also auch folgendermaßen definieren:

Drehmomente verursachen eine Änderung der Drehbewegung.

Hebelgesetz und Drehmoment

Eine Rotationsbewegung erfolgt um eine Achse. Das kann eine feste Achse sein, die z.B. durch Lager festgehalten wird, wie man es bei Fahrrädern oder Autos kennt, oder aber eine „freie Achse“, wie wenn ein Fußball sich während seines Flugs nicht nur translatorisch bewegt, sondern sich auch um die eigene Achse dreht. Bei einem kugelförmigen Ball entspricht dabei jeder Durchmesser einer sogenannten Hauptträgheitsachse, um die eine Drehung erfolgen kann.

Als Hebel wiederum bezeichnet man einfach einen starren Körper, der sich um einen Drehpunkt dreht. In Modellform werden Hebel sehr oft als stabförmige Körper, die sich um eine feste Achse drehen, dargestellt (einer Wippe nachempfunden), wobei in Realität ein Hebel die unterschiedlichsten Formen haben kann. Von einer langen Stange wie bei einer Wippe, einem geknickten Hebel, einem einseitigen Hebel, einer Scheibe oder auch ganz anderen beliebigen Formen. Aus mechanischer Sicht fungieren Hebel als sogenannte Kraftwandler, mithilfe derer die Richtung und/oder den Betrag von Kräften geändert werden kann. So werden Heben beispielsweise dazu genutzt, um mit einer kleinen Kraft einen Körper mit großem Gewicht zu heben, oder durch einen längeren Schraubenschlüssel Muttern einfacher fester ziehen und einfacher lockern zu können. Die Funktionsweise dahinter wird vom Hebelgesetz aufgegriffen, welches erstmals in der Antike von Archimedes formuliert wurde. Beschreibungen von Hebeln finden sich aber bereits in früheren Schriften, aus der Schule des Aristoteles. Das Hebelgesetz besagt, dass die Krafteinwirkung am Drehpunkt (Drehmoment) umso größer ausfällt, je länger der Hebel ist. Archimedes formulierte dies in seinem berühmten Satz: Gebt mir einen festen Punkt, und ich hebe die Welt aus den Angeln.

Sobald ein Hebel durch eine definierte Kraft an einem Ende bewegt wird, erzeugt er am Drehpunkt eine messbare Kraft. Und diese erzielte Kraft wird wie gesagt als Drehmoment bezeichnet und in Newtonmeter (Nm) angegeben (1Nm = 1N Kraft, welche mit einem Hebelarm von 1 m Länge am Drehpunkt eines Körpers einwirkt). Ein Drehmoment M ist also bei einem drehbaren Hebel die Ursache für dessen Winkelbeschleunigung ∆ω/∆t. Diese ist zum Drehmoment M proportional. Die Bezeichnung als Kraftwandler kommt daher, weil nicht nur die Kraft, sondern eben auch der Kraftangriffspunkt darüber entscheiden, wie stark das erzeugte Drehmoment am Drehpunkt ist. So ist das Drehmoment M das Produkt aus Hebelarm und Kraft, was bedeutet, dass bei einer noch so kleinen Kraft ein theoretisch beliebig hohes Drehmoment erreicht werden kann, wenn nur der Hebelarm lang genug ist.

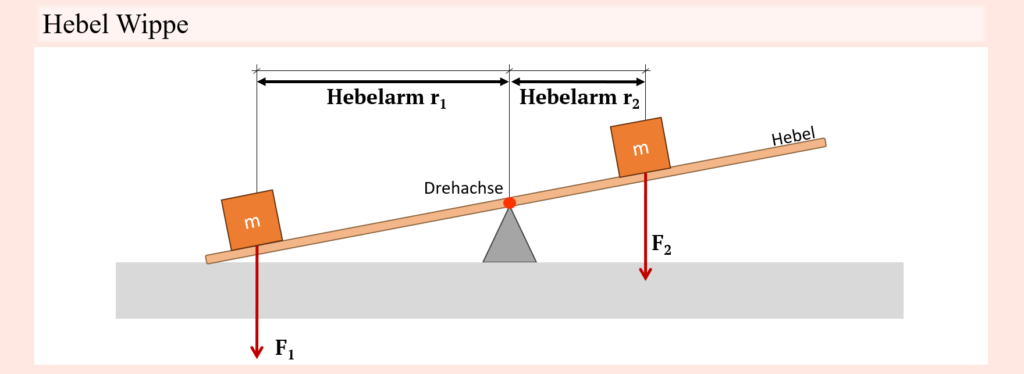
Wichtig zu beachten ist dabei aber, dass in das Drehmoment nicht der Abstand P des Angriffspunkts der Kraft vom Drehpunkt D eingeht, sondern der Abstand des Drehpunkts senkrecht zur Wirkungslinie der Kraft. Diesen Abstand nennt man Hebelarm (nicht zu verwechseln mit dem Hebel selbst), manchmal auch Kraftarm, manchmal auch Lastarm. Um keine Missverständnisse zu schüren, bleiben wir aber stets bei Hebelarm.

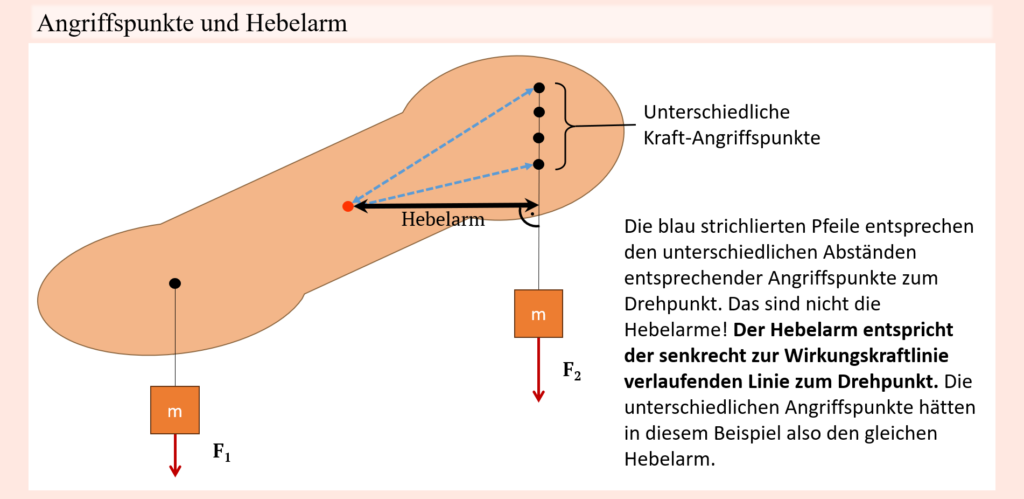
Das hat zur Folge, dass eine Kraft, die bei einem Körper, welcher sich um eine Drehachse dreht, an einem bestimmten Punkt angreift und in eine bestimmte Richtung verläuft, bei unterschiedlichem Drehwinkel einen verschieden langen Hebelarm aufweist und folglich ein unterschiedliches Drehmoment erzeugt. Genauer gesagt ist der Betrag des Drehmoments maximal, wenn die Kraft F senkrecht zur Strecke s zwischen Angriffspunkt und Drehachse auf den Körper einwirkt (sodass der Abstand des Kraftangriffspunkts zum Drehpunkt = der senkrechte Abstand von der Wirkungskraftlinie zum Drehpunkt). Wirkt die Kraft hingegen entlang dieser Verbindungslinie, so ist der Betrag des Drehmoments gleich null (der Körper wird in keine Drehung versetzt). Passiert dies im Falle eines freien Körpers, dann wird dieser durch jene Krafteinwirkung als Ganzes bewegt (translatorisch), wohingegen ein fixierter Körper sich nicht bewegt (evtl. verformt).

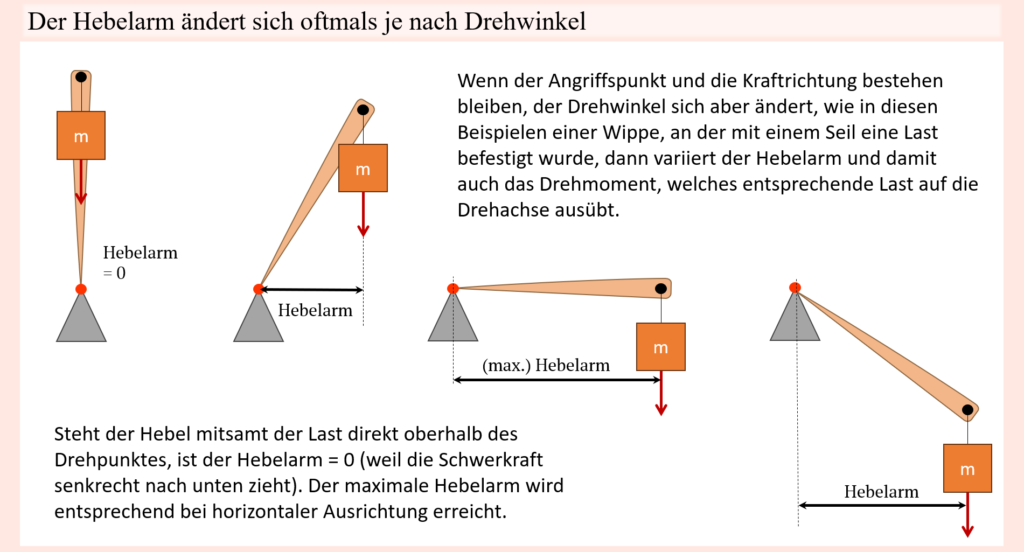
Mithilfe der Kräftezerlegung kann man jeden Kraftvektor, der mit einem Abstand x an einem starren Körper angreift, also grundlegend in zwei Kraftkomponenten zerlegen, die unterschiedliche Wirkungen haben:

Die Wirklinie der Kraftkomponente F₁geht durch den Drehpunkt. Diese Komponente übt zwar Kraft auf die Drehachse aus, bewirkt aber keine Drehung.
Im Unterschied dazu ist die Kraftkomponente F₁für die Drehung des starren Körpers zuständig.

Hier bestätigt sich dann auch nochmal die obige Behauptung, dass man nämlich für α = 90° maximales Drehmoment erhält, wohingegen für jeden anderen Winkel das Drehmoment kleiner ist und für α = 0° das Drehmoment schließlich null ist.

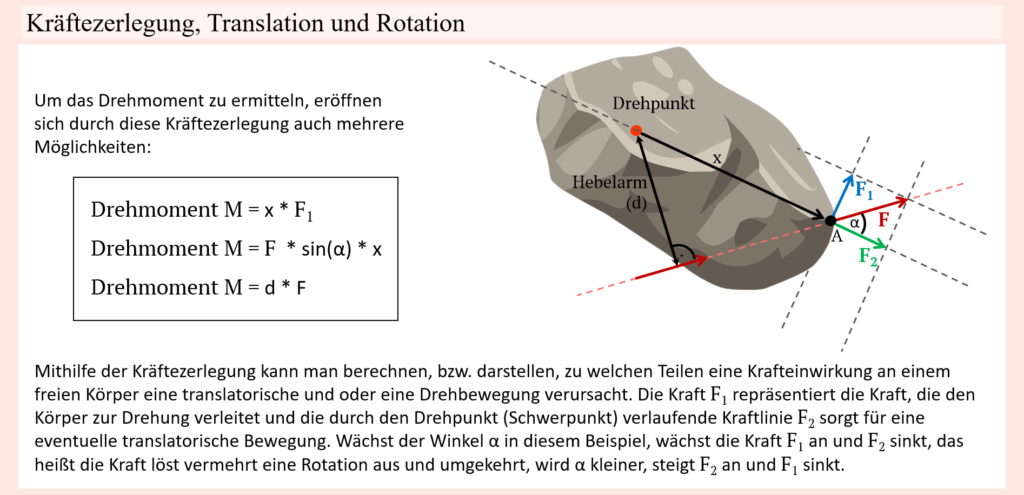
Richtung des Drehmoments

Auch wenn es um einen Körper geht, der über seine Drehachse(n) in verschiedenste Richtungen gedreht werden kann, wirkt ein einzelnes Drehmoment in einer einzelnen Ebene, weswegen es grundsätzlich ausreichend, diese Ebene zu betrachten. Das jeweilige Drehmoment kann dann durch eine einzelne Zahl angegeben werden, deren Vorzeichen den Drehsinn angibt. Je nach Richtung der angreifenden Kraft ergibt sich so eine rechtsdrehende oder linksdrehende Wirkung. Das Vorzeichen folgt der mathematischen Konvention für Drehrichtungen. Dabei gilt: eine Linksdrehung = positives Vorzeichen („gegen den Uhrzeigersinn“) und eine Rechtsdrehung = negatives Vorzeichen („im Uhrzeigersinn“). Dementsprechend könnte man auch von einem „linksdrehenden Drehmoment“ sprechen, wenn das Drehmoment einen ruhenden Körper in eine Drehung entgegen dem Uhrzeigersinn versetzt, und von einem „rechtsdrehenden Drehmoment“, wenn das Drehmoment einen ruhenden Körper in eine Drehung im Uhrzeigersinn versetzt.

Genau genommen sind diese Bezeichnungen aber eigentlich nicht ganz korrekt, weil ein Drehmoment weder nach links noch nach rechts dreht. Ähnlich wie eine Bewegung keine Kraft erfordert (wenn sie einmal in Gang gekommen ist), erfordert auch eine Drehung kein Drehmoment. Wie die Kraft für eine Beschleunigung ist das Drehmoment für eine Winkelbeschleunigung verantwortlich.

Einseitige und zweiseitige Hebel

An einem zweiseitigen Hebel liegen die Angriffspunkte der Kräfte, von der Drehachse aus betrachtet, auf verschiedenen Seiten des Hebels. Der Hebel ist im Gleichgewicht, wenn das Drehmoment auf der linken Seite des Hebels dem Drehmoment auf der rechten Seite des Hebels entspricht. Ist das wirkende Drehmoment auf der einen Seite größer als auf der anderen, so führt die Hebelstange eine entsprechende Rotation um die Drehachse aus.

An einem einseitigen Hebel liegt die Drehachse am Rand der Hebelstange, so dass die Angriffspunkte aller wirkenden Kräfte, von der Drehachse aus betrachtet, auf der gleichen Seite des Hebels liegen. Damit an einem einseitigen Hebel ein Gleichgewicht herrschen kann, muss wiederum die Summe der linksdrehenden Drehmomente gleich der Summe der rechtsdrehenden Drehmomente entsprechen. Dazu müssen die auf einen einseitigen Hebel einwirkenden Kräfte in entgegengesetzte Richtungen zeigen.

Drehmoment und Gleichgewicht

Das Drehmoment ist für Drehbewegungen wie gesagt so, wie die Kraft für translatorische Bewegungen. Wenn also mehrere Drehmomente auf einen drehbar gelagerten Körper einwirken, dann ist das Gesamtdrehmoment die Summe der einzelnen Drehmomente.

Im Sinne des Gleichgewichtes bedeutet dies, wie auch beim obig angesprochenen Kräftegleichgewicht, dass sich ein Hebel laut Hebelgesetz immer dann im Gleichgewicht befindet, wenn sich alle an ihm wirkenden Drehmomente gegenseitig ausgleichen, oder anders ausgedrückt linksdrehendes Drehmoment = rechtsdrehendes Drehmoment ist, sodass das insgesamte Drehmoment = 0.

Schwerpunkt und Auflagefläche

Ein gutes Beispiel, um die Rolle der Wirkungskraftlinie im Verhältnis zum Drehpunkt zu veranschaulichen, kann auch ein frei stehenden Körper sein. Ein frei stehender Körper, an dem keine Kräfte von außen einwirken, kippt nicht um, solange sich sein Schwerpunkt oberhalb der Auflagefläche befindet. Der Schwerpunkt fungiert hier wohlgemerkt als Wirkungskraftlinie. Physikalisch gesprochen ist der Schwerpunkt nämlich das mit der Masse gewichtete Mittel des Körpers und kann demnach als Wirkungslinie seiner Gewichtskraft angesehen werden.

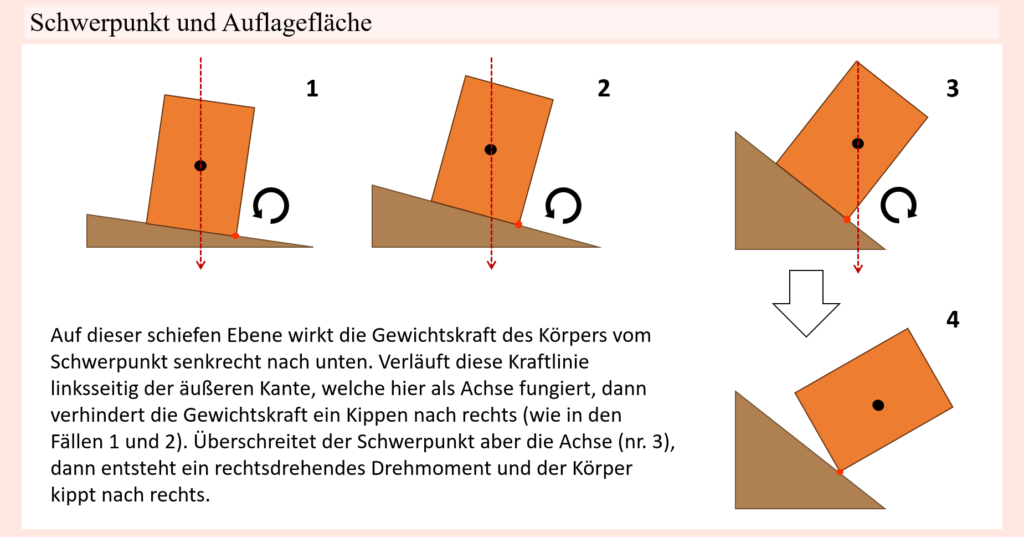
Neigt man den Körper nun (sei es durch simples Anheben oder z.B. durch einen schiefen Untergrund), dann kippt der Körper nicht um, solange der Schwerpunkt die Auflagefläche nicht überschreitet. Bei einer weiteren Auslenkung überschreitet die vom Schwerpunkt aus senkrecht nach unten gezogene Linie die Grenze der Auflagefläche. Sobald dies der Fall ist, kippt der Körper um, wobei die äußere Kante der Auflagefläche als Drehachse angesehen werden kann.

Ähnliches gilt, wenn eine horizontale Kraft auf einer bestimmten Höhe über der Standfläche des Körpers auf diesen einwirkt und dadurch ein „Kipp-Drehmoment“ erzeugt, wohingegen die Gewichtskraft im Schwerpunkt im entgegengesetzten Drehsinn ein „Stand-Drehmoment“ bewirkt. Ist das erzeugte „Kipp-Drehmoment“ größer als „Stand-Drehmoment“ kippt die einwirkende Kraft den Körper um.

Kraftwandler und Getriebe

Abschließend zum Thema rund um Drehmomente wollen wir noch kurz auf einige Anwendungszwecke eingehen, welche das Aufkommen von Hebeln und Drehmomenten in der Realität verdeutlichen, denn dies kann durch vorwiegende Betrachtung von Hebeln in Form von Wippen, welche hilfreich für das Verständnis der Funktionsweise sind, etwas untergehen. Grundsätzlich kann sich jeder Körper um bestimmte Achsen drehen, was zum Beispiel durch das obige Beispiel beim Umkippen eines Körpers ersichtlich wird. Aber auch steife Körper, die sich um fixe Achsen drehen, finden sich häufig. Das für uns wesentlichste Beispiel ist hier der menschliche Bewegungsapparat, wo sich die Knochen um Gelenke drehen, und somit Knochen als Hebel und Gelenke als Drehpunkte fungieren. Intrinsisch verursachte Bewegungen (durch Muskulatur) können nämlich nicht rein translatorisch ablaufen, weswegen die Bewegung von Tieren auch immer auf Rotationsbewegungen aufbaut.

Aber auch in unserem Alltag machen wir uns Hebel und Drehmomente oft zu nutzen, denn als Kraftwandler ist es damit möglich, die Richtung und/oder den Betrag von Kräften zu ändern. Neben Hebeln sind andere wichtige Beispiele für „Kraftwandler“ z.B. feste und lose Rollen, Flaschenzüge oder auch geneigte Ebenen. All diese Techniken werden in komplexeren Maschinen in vielfacher Weise miteinander kombiniert. Zusätzlich werden in Maschinen auch häufig Getriebe, insbesondere Zahnrad- und Riemengetriebe, eingebaut, welche als „Drehmomentwandler“ fungieren. Bei diesen Einrichtungen bleiben die Kräfte bei der Übertragung von einem Objekt zum nächsten unverändert. Die wirkenden Drehmomente und die erreichte Drehzahl ändern sich allerdings, da die rotierenden Objekte (normalerweise) unterschiedliche Radien aufweisen, sodass das erzeugte Drehmoment, die Drehzahl und teilweise auch die Drehrichtung nach Bedarf verändert werden können. Dies kennen wir zum Beispiel von Autos oder auch von einem herkömmlichen Fahrrad, wo jeweils zwischen dem Antrieb (Motor bzw. Fußpedale) und dem Antrieb im Sinne der rotierenden Räder, die das Fahrzeug bewegen, ein Getriebe zwischengeschaltet ist.

Werden mehrere Zahnräder miteinander kombiniert, so bezeichnet man die Konstruktion als Getriebe. Zwei Räder wirken dabei stets mit gleich großer Kraft aufeinander ein. Sind allerdings die Radien der Zahnräder unterschiedlich groß, so sind jeweils auch die wirkenden Drehmomente verschieden. Damit stehen die erzeugten Drehmomente im gleichen Größenverhältnis wie die Radien der aufeinander einwirkenden Zahnräder. Zusätzlich ist die Anzahl an Zahnungen ebenso proportional zum Radius. All das bedeutet, dass wenn zwei Zahnräder zusammenwirken, wobei das erste den doppelten Radius des zweiten Zahnrades aufweist, das erzeugte Drehmoment beim zweiten Zahnrad nur halb so groß ist, dieses sich aber doppelt so schnell dreht (da die Zahnräder ineinandergreifen, benötigt das Zahnrad mit nur halb so vielen Zähnen doppelt so oft).

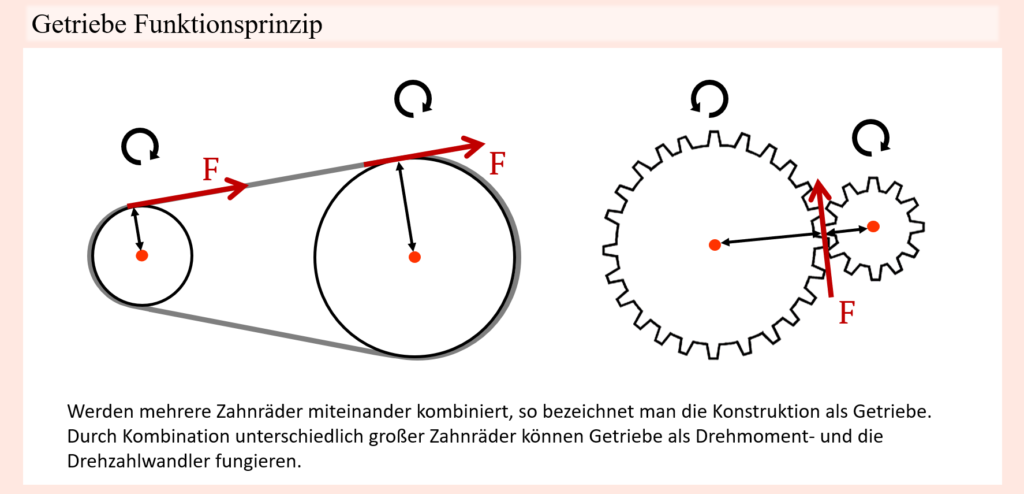
Beim Fahrrad macht man sich dies zu Nutze, um mit einer angemessenen Tretgeschwindigkeit trotzdem eine hohe Drehzahl des Antriebsrades zu erreichen. Würde man mit den Pedalen direkt das Hinterrad antreiben, dann müsse die Tretgeschwindigkeit gleich der Drehzahl des Hinterrades sein, man müsste also mit den Pedalen eine Umdrehung durchführen, um am Hinterrad eine Umdrehung auszulösen. Würde man nur im Schritttempo fahren, ginge das vielleicht noch grad so, aber wenn man mal annimmt man fährt mit 18 km/h, was umgerechnet 5 m/s sind und das Hinterrad sagen wir 2,5 Umdrehungen pro s dafür benötigt, dann würde das auch 2,5 Umdrehungen der Pedale pro Sekunde (150/min) erfordern, was alles andere als angenehm wäre. Dieses Problem wird durch das Getriebe gelöst, indem die Pedale ein größeres Zahnrad antreiben, welches wiederum mittels einer Kette in Verbindung mit einem kleinen Zahnrad an der Achse des Hinterrades steht. Auf diese Weise kann die Pedalumdrehung in eine höhere Drehzahl am Antriebsrad übersetzt werden. Wohlgemerkt reduziert man dabei das Drehmoment (geringerer Radius = geringerer Hebelarm), aber das ist sekundär, schließlich ist der wesentliche Zweck eine zumutbare Tretgeschwindigkeit bei einer vernünftigen Fahrgeschwindigkeit zu erreichen. Fährt man aber eine Steigung hoch, dann braucht man mehr Drehmoment, dies erreicht man durch das Einlegen eines anderen Ganges, wodurch der Radius am hinteren Zahnrad größer gewählt wird. So kommt man dann zwar leichter Bergauf, man muss bei gleicher Fahrgeschwindigkeit aber schneller treten.

Auch beim PKW macht man sich solch ein Getriebe zu Nutze, wobei die Gangschaltung es wie auch beim Fahrrad ermöglicht zwischen verschiedenen Übersetzungsverhältnissen zu wechseln. So erzeugt man im 1. Gang ein im Vergleich sehr großes Drehmoment an der angetriebenen Achse bei geringer Drehzahl, welches ermöglicht aus der Ruhe stark zu beschleunigen oder zum Beispiel eine starke Steigung hochzufahren. Und im 5. Gang erzeugt man hingegen ein kleineres Drehmoment an der angetriebenen Achse, aber bei hoher Drehzahl.

Mechanik der Erhaltungssätze

Physikalische Theorien sind wie gesagt daran versucht, immer zutreffendere Beschreibungen und daraus resultierende Vorhersagen der Natur zu geben. Dabei beziehen sie sich gemäß der Galileischen Methode auf bestimmte (messbaren) Eigenschaften, die einem Naturphänomen entnommen werden und stellen diese in einen generellen Kontext, so wie Newton es mit Bewegung, Beschleunigung und Kraft gemacht hat. Diese wissenschaftliche Methode hat gleichzeitig aber auch zu Folge, dass manche physikalischen Sachverhalte auf einige verschiedene Weisen erklärt werden können. Bis zu diesem Punkt haben wir dementsprechend vor allem die Newtonsche Mechanik als eine der Erklärungsmöglichkeiten von Bewegungen kennengelernt, wobei diese als Werkzeug in der Biomechanik auch meistens ausreicht. Dennoch ist es erwähnenswert eine andere Herangehensweise, nämlich über die „Mechanik der Erhaltungssätze“ zu betrachten, weil diese im Wesentlichen die Aussagen der Newtonschen Mechanik ebenso enthalten, nur eben übersetzt in andere Größen und dadurch sogar vermag einige Probleme zu lösen. Das Bemerkenswerte dabei ist, dass obwohl mit diesen sogenannten Erhaltungsgrößen teils das gleiche erklärt wird, dabei Beschleunigungen und Kräfte gar nicht vorkommen, vielmehr geht es um ganz andere Größen wie den Impuls p und die Energie E.

Wie „Mechanik der Erhaltungssätze“ bereits erahnen lässt, beruht diese Methode erstmals auf anderen Anhaltspunkten wie etwa die Newtonsche Mechanik, genauer gesagt baut sie auf der Beobachtung auf, dass bestimmte Größen innerhalb eines physikalischen Systems erhalten bleiben, sich also nicht ändern. Solche Größen kann man auch als Erhaltungsgrößen bezeichnen und für sie gelten die sogenannten Erhaltungssätze. Solche Erhaltungssätze geben Auskunft über ganz wesentliche Eigenschaften von physikalischen Systemen und ermöglichen dadurch Vorhersagen. So zum Beispiel der Energieerhaltungssatz und der Impulserhaltungssatz. Interagieren beispielsweise zwei Körper miteinander, dann verändern sich deren Zustandsgrößen im Laufe der Bewegung, wohingegen die Erhaltungsgrößen konstant bleiben. Diese Erhaltungsgrößen, welche sich aus den jeweiligen Zustandsgrößen berechnen, geben in diesem Sinne Rückschlüsse darauf, wie sich die Zustandsgrößen im Verhältnis zueinander verändern müssen. Wenn man das so liest, mag es vielleicht etwas un-aussagekräftig erscheinen, aber bei der Gegenüberstellung mit der Newtonschen Mechanik weiter unten sollte das Prinzip deutlich werden. Bevor wir aber dazu kommen, müssen wir kurz die beiden relevantesten Größen einführen, die hier jetzt hinzukommen, nämlich Energie und Impuls.

Die Energie ist eine fiktive Größe und gibt in der klassischen Mechanik die Fähigkeit eines Systems wieder, Arbeit zu verrichten. Doch was bedeutet das? Physikalische Arbeit ist das Produkt aus einer Kraft F über eine Strecke s und beschreibt, dass wenn man zum Beispiel einen Körper auf eine 1 m hohe Ladefläche eines Fahrzeuges anheben möchte, man eine gewisse Arbeit verrichten muss. Um dies zu erreichen, kann man verschiedenste Methoden anwenden. Man könnte den Körper schlichtweg in die Hand nehmen und senkrecht nach oben anheben, man könnte eine Rampe nutzen und ihn auf einem Rollbrett die schiefe Ebene hochziehen oder man könnte sogar einen Flaschenzug verwenden. All diese Methoden haben vor und Nachteile. Hebt man den Körper per Hand einfach hoch, dann muss man die kurz möglichste Strecke zurücklegen, andererseits muss man auch viel Kraft aufwenden. Würde man den Körper im Gegenzug eine schiefe Ebene hochziehen, dann müsste man nur noch die Hangabtriebskraft überwinden, welche, wie wir oben gesehen haben, ja geringer ausfällt, desto geringer der Steigungswinkel ist, andererseits würde dann aber die Strecke, welche zurückgelegt werden muss, proportional ansteigen. Selbes gilt im Falle eines Seilzuges, wo man sich durch mehrere tragende Seile, an denen man den Körper hochzieht, Kraft sparen kann, aber andererseits wieder mehr Strecke zurücklegen muss. In Summe, egal wie man es dreht und wendet, bleibt die physikalische Arbeit, die verrichtet werden muss bestehen, man kann zwar Kraft einsparen, aber diesen eventuellen Vorteil muss man sich durch einen längeren Weg erkaufen. Vielleicht genügt also die halbe Kraft, um den Körper über eine schiefe Ebene nach oben zu ziehen, aber dann legt man die doppelte Strecke zurück. So schön, so gut, aber wie kommen wir hiervon jetzt zur Energie?

Wenn wir z.B. einen Körper A auf eine bestimmte Höhe h anheben, dann müssen wir eine gewisse Menge an Arbeit hineinstecken, lässt man den Körper nun aber auf der Höhe h los, kehrt sich der Vorgang um, sprich der Körper fällt um die Höhe h herunter und kann dabei wieder Arbeit verrichten, indem er z.B. einen anderen Körper B bewegt (das Prinzip kann man sich z.B. mit einem Wasserrad vorstellen. Wasser wird zunächst durch einen Arbeitsaufwand an eine erhöhte Position gebracht und kann dann, wenn es wieder nach unten strömt, Arbeit an einem Wasserrad verrichten, dieses also antreiben). Dieses „etwas“, das den Körper dazu befähigt, Arbeit zu leisten, wird in der Physik als Energie bezeichnet. Durch das Anheben wurde Arbeit am Körper A verrichtet, die in dem Körper als zusätzliche Energie gespeichert wird. Beim Herunterfallen wird diese „Höhenenergie“ kontinuierlich in Bewegungsenergie umgewandelt. Hier werden auch die zwei wichtigsten Energieformen für die Mechanik ersichtlich, nämlich die sogenannte Lageenergie (Höhenenergie), welche die Energie eines Körpers in einer bestimmten Position im Raum beschreibt, vor allem seiner Höhe, sowie die kinetische Energie (Bewegungsenergie), welche daraus resultiert, dass ein Körper beschleunigt werden muss, um schneller zu werden, was dann als Bewegungsenergie im Körper gespeichert ist. Wie gesagt Energie ist eine fiktive Größe und steht stellvertretend für den jeweiligen Zustand des Körpers und seiner gegenwärtigen Fähigkeit Arbeit zu verrichten. Die Energie kann also als „gespeicherte Arbeit“ angesehen werden. So haben Arbeit und Energie auch dieselbe Einheit (Joule bzw. Newton-Meter) und Arbeit ist dementsprechend als eine Austauschform von Energie zu betrachten.

Der Energieerhaltungssatz besagt hierbei, dass in einem geschlossenen System die Menge an Energie konstant bleibt, also weder verbraucht noch gesteigert werden kann. Betrachtete man also zwei Körper als ein System, bedeutet dies, dass zwar Arbeit vom einen am anderen ausgeführt werden kann, dies aber vielmehr einem Energieaustausch von einem zum andern entspricht, sodass sich die Gesamtenergie sich nicht ändert.

So gesehen ist der Energieerhaltungssatz der wichtigste Erhaltungssatz der Physik. Für uns beschreibt er zum Beispiel, dass wir in unseren Muskeln chemische Energie von Nährstoffen in Bewegungsenergie umwandeln und diese nutzen, um Arbeit zu leisten. Ein sehr anschauliches mechanisches Beispiel des Energieerhaltungssatzes ist hingegen ein Pendel. Vernachlässigt man bei einem Pendel, die Reibung, dann ändert sich die Summe von Lageenergie und kinetischer Energie nicht mit der Zeit. Lenkt man das Pendel aus, so schwingt es zwischen zwei Umkehrpunkten und erreicht seine höchste Geschwindigkeit am Ort des Potentialminimums (geringste Lageenergie). An den Umkehrpunkten ist die kinetische Energie null und die Lageenergie maximal. Unabhängig von der Position des Pendels hat die Summe aus kinetischer Energie und Lageenergie den durch die anfängliche Auslenkung vorgegebenen Wert.

Nun gut, kommen wir zum Impuls. Der Impuls ist wiederum die mechanische Größe, die den Bewegungszustand eines Körpers der Masse m, der sich mit der Geschwindigkeit v bewegt, wiedergibt (Impuls p=mv) und analog zur Geschwindigkeit in Bewegungsrichtung zeigt (also auch ein Vektor ist). Der Impuls eines physikalischen Objekts ist also umso größer, je schneller es sich bewegt und je größer seine Masse (Trägheit) ist. Damit steht der Impuls für das, was in der Umgangssprache unscharf mit „Schwung“ bezeichnet wird (erinnert an den mittelalterlichen Begriff des Impetus). Und der Impulserhaltungssatz besagt, dass der Gesamtimpuls eines Systems konstant bleibt, wenn keine äußere Einwirkung stattfindet. (Auch hier gelten analoge Größen und Erhaltungssätze für Drehbewegungen, der Drehimpuls und Drehimpulserhaltung.)

Sehen wir uns hierzu einige Verbindungen zu der Newtonschen Mechanik an.

Das 1. Newton-Gesetz besagt, dass wenn keine äußeren Kräfte wirken, die Geschwindigkeit eines Körpers nach Betrag und Richtung konstant bleibt. Aus dem Impulserhaltungssatz wiederum folgt, dass der Betrag und die Richtung des Impulses erhalten bleibt, wenn das System geschlossen ist (also nichts von außen eine Impulsänderung verursacht). In beiden Fällen folgt also, dass sich ein bereits bewegender Körper geradeaus mit konstanter Geschwindigkeit weiterbewegt und ein ruhender Körper in Ruhe bleibt. Gibt man z.B. mit dem Auto kurz Gas, dann bewirken Reibungskräfte, dass der Impuls des Wagens langsam abnimmt, ohne Reibung und andere Kräfte bliebe er konstant und der Wagen würde seinen „Schwung“ nicht verlieren und in Bewegung bleiben (wie auch 1. bzw. 2. Gesetz von Newton). Ein konstanter Impuls ist demnach gleichzusetzen mit F = 0, bzw. eine Impulsänderung mit einer Krafteinwirkung, was man auch einfach ableiten kann, denn bei konstanter von 0 verschiedener Masse gilt nämlich ∆p/∆t = m ∆v/∆t = ma = F. Deswegen kann die Formel F = ma auch dargestellt werden als F = ∆p/∆t.

Diese Schreibweise des 2. Newtonschen Gesetzes ist heutzutage gängig, weil sie auch bei hohen Geschwindigkeiten gültig bleibt. Das ist wichtig, weil wir heute wissen, dass die Lichtgeschwindigkeit die Maximalgeschwindigkeit in unserem Universum ist. Nach der klassischen Formulierung des Aktionsprinzips, würde eine konstante Kraft aber auch eine konstante Beschleunigung bewirken, die nach einiger Zeit dazu führt, dass die Geschwindigkeit eines Körpers die Lichtgeschwindigkeit überschreitet. Das steht aber im Widerspruch zu Einsteins Relativitätstheorie, nach der sich nichts schneller als das Licht fortbewegen kann. Definiert man eine Kraft aber als F = ∆p/∆t dann kann dieses Problem gelöst werden, weil der Impuls im Gegensatz zur Geschwindigkeit beliebig hoch ansteigen kann (die Trägheit wird mit wachsender Geschwindigkeit aber auch immer größer, sodass das Objekt immer schwieriger ist, weiter zu beschleunigen und daher die Lichtgeschwindigkeit nie überschritten werden kann).

Aus dem dritten newtonschen Gesetz folgt, wenn Körper A mit einem anderen Körper B zusammenstößt und eine Kraft F₁ ausübt, der Körper B eine genau entgegengesetzte Kraft F₂ auf Körper A ausübt. Auch das stimmt mit dem Impulserhaltungssatz überein, welches ohne äußere Einwirkung besagt, dass der Impuls von Körper A p₁ + der Impuls von Körper B p₂ = konstant ist. Wenn die Körper zusammenstoßen bedeutet das, dass die dadurch ausgelösten Impulsänderungen ∆p₁/∆t + ∆p₂/∆t = 0 ergeben, was wiederum die beiden Kräfte F₁ und F₂ in Beziehung zueinander setzt, schließlich sind jene Kräfte die Ursache für die Impulsänderungen.

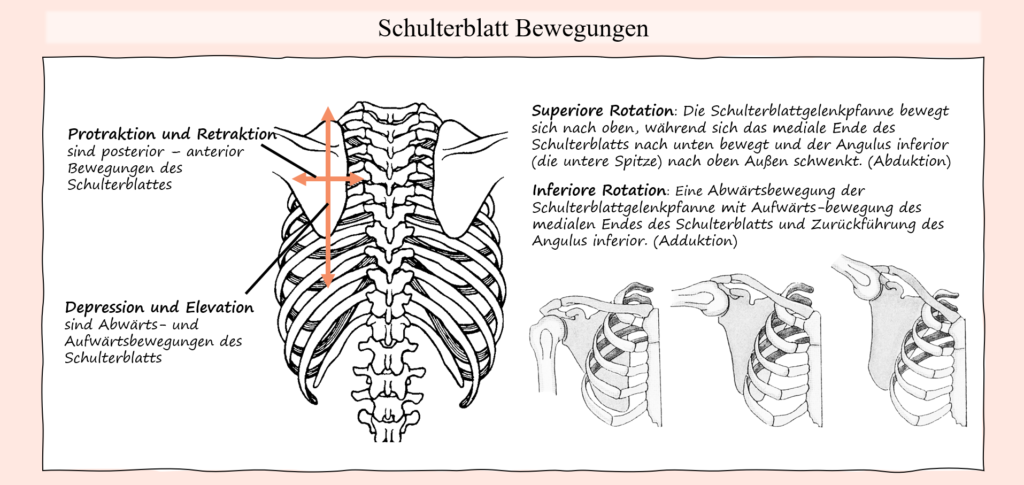
Ellbogen

Der Ellbogen ist die Verbindung des Oberarms mit dem Unterarm und setzt sich aus drei Knochen zusammen, dem Humerus (Oberarmknochen), der Ulna (Elle) sowie dem Radius (Speiche). Das Ellenbogengelenk als Ganzes hat die Aufgabe, die Beweglichkeit dieser Knochen gegeneinander zu gewährleisten.

Dabei entspricht das eigentliche Ellenbogengelenk einem klassischen, einachsigen Scharniergelenk, das vom Humeroulnargelenk (Oberarm-Ellen-Gelenk), der Verbindung zwischen Oberarmknochen und der Ulna, gebildet wird. Dieses Gelenk erfüllt die wesentliche Funktion des Ellbogens, nämlich die Flexion und Extension. Dennoch ist dies nicht die einzig mögliche Bewegung im Ellbogengelenk, denn schließlich sind wir auch dazu in der Lage unsere Hand, oder vielmehr unseren Unterarm zu rotieren (Pronation/ Supination). Um das zu gewährleisten, kommen zwei weitere Gelenke ins Spiel.

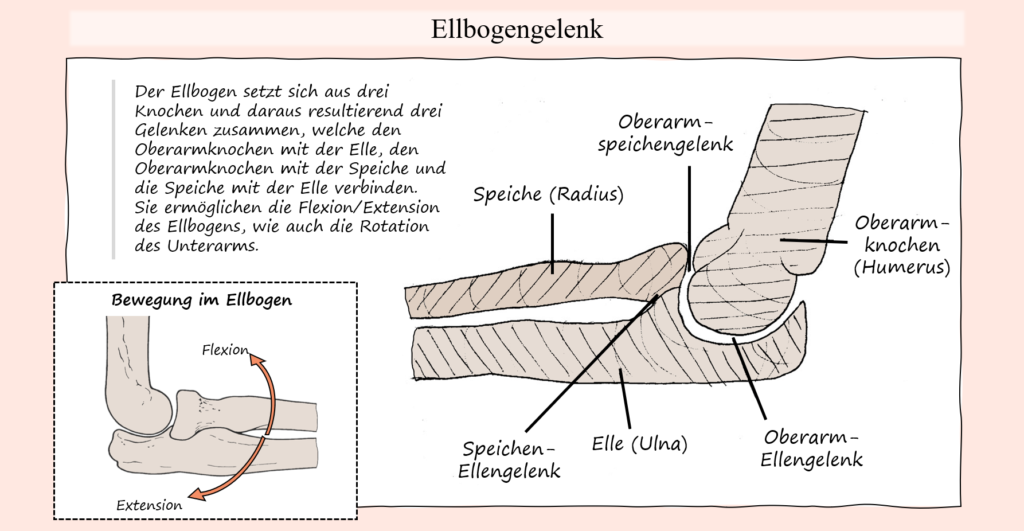
Mit dem Begriff „Ellenbogen“ sind demnach auch das Humeroradialgelenk (Oberarm, -Speichen-Gelenk) und das proximale Radioulnargelenk (Speichen-Ellen-Gelenk) verbunden, auch hier spricht man also von einem zusammengesetzten Gelenk. Alle drei dieser Gelenke sind von einer einzigen Gelenkkapsel umgeben.

Das Humeroradialgelenk erlaubt Supinations- und Pronationsbewegungen sowie Extension und Flexion). Dabei handelt es sich anatomisch um ein Kugelgelenk, wobei seitliche Bewegungen jedoch durch die Fesselung des Radius an der Ulna ausgeschlossen sind (sodass es funktionell nur noch eine Bewegungsachse hat).

Durch das Radioulnargelenk gleitet der Radius bei Pronationsbewegungen wie ein Rad in der entsprechenden Gelenkpfanne der Ulna. Die Pfanne dieses Gelenkes ist klein und ebenfalls überknorpelt, sie wird durch ein Band zu einem Ring ergänzt, in dem sich der Kopf um die Unterarmachse dreht.

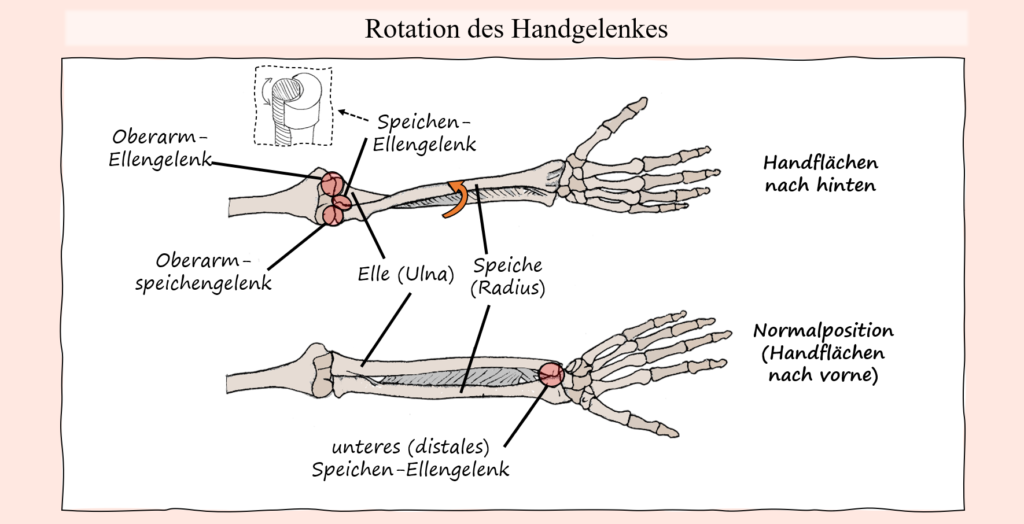
Handgelenk

Die menschliche Hand, inklusive des Handgelenks, der Handfläche sowie den Fingern, weist eine sehr hohe Bewegungsvielfalt auf. Dieses hohe Maß an Bewegung wird zum einen durch sehr viele Einzelteile, also vielen kleinen Knochen, aus denen sich die Hand zusammensetzt, und zum anderen durch viele Muskeln, die diese Knochen bewegen und sich nicht nur über die Hand, sondern auch den Unterarm ausbreiten, gewährleistet. Wie gesagt werden wir auf jene Muskeln nicht im Detail eingehen, aber das funktionelle Verhältnis der knöchernen Strukturen mit den sie umgebenden Muskeln bleibt natürlich auch hier dasselbe.

Aus welchen beiden Knochen der Unterarm besteht, haben wir ja bereits gesehen. Die knöchernen Komponenten der Hand kann man in drei Gruppen unterteilen, den Handwurzelknochen, welche zwei Reihen bilden, den Mittelhandknochen und den Fingerknochen. Als „Handgelenk“ bezeichnet man zusammengefasst vor allem zwei Gelenke, zum einen die Verbindung der proximalen Handwurzelknochen mit dem Unterarm (Radiokarpalgelenk) und zum anderen die Verbindung zwischen der proximalen und der distalen Reihe der Handwurzelknochen (Mediokarpalgelenk).

Die Radiokarpalgelenk bezeichnet das Gelenk zwischen dem distalen Ende der Speiche (Radius) und drei der proximalen Handwurzelknochen. Hinzukommt die Zwischengelenkscheibe des distalen Radioulnargelenks (Speichen-Ellen-Gelenkes), welches auch an der Gelenkbildung des proximalen Handgelenkes beteiligt ist. Funktionell gesehen handelt es sich dabei um ein Ei-Gelenk und ermöglicht so zwei Bewegungsachsen, was wiederum eine Palmarflexion und Dorsalextension sowie Radialabduktion und Ulnarabduktion ermöglicht.

Das Mediokarpalgelenk bezeichnet den Gelenkspalt zwischen der proximalen und der distalen Reihe der Handwurzelknochen und setzt sich anatomisch aus den einzelnen Gelenken zwischen jeweils zwei benachbarten Knochen zusammen, wirkt funktionell aber als Einheit.

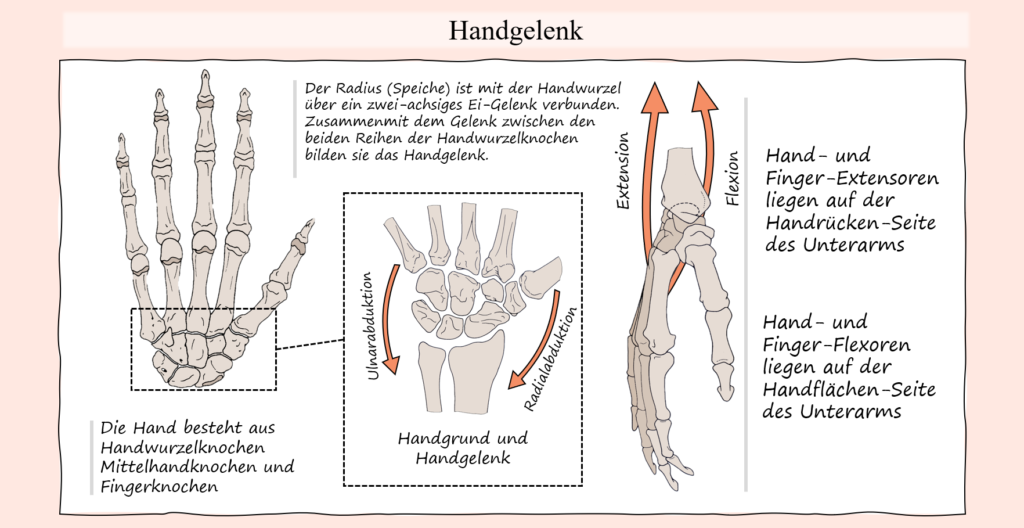
Muskeln, die den Schultergürtel positionieren

Die Muskeln der Schulter und der oberen Extremität können wie gesagt in vier Gruppen eingeteilt werden, Muskeln, die den Brustgürtel stabilisieren und positionieren, Muskeln, die den Arm bewegen, Muskeln, die den Unterarm bewegen, und Muskeln, die die Handgelenke, Hände und Finger bewegen.

Bei Muskeln, die den Schultergürtel positionieren, geht es im Grunde um Muskeln, welche direkt am Schultergürtel, also am Schulterblatt oder Schlüsselbein ziehen und so dessen Positionierung aktiv beeinflussen. „Aktiv“ deswegen, weil auch zum Beispiel Muskeln, welche am Oberarmknochen ansetzen und demnach das Glenohumeralgelenk kontrollieren, gleichzeitig auch den ganzen Schultergürtel indirekt beeinflussen, weil die jeweiligen Anteile funktionell verbunden sind. Die Muskeln, welche den Schultergürtel aktiv positionieren, befinden sich entweder am vorderen Brustkorb oder am hinteren Brustkorb. Zu den hinteren Muskeln gehören der Trapezius, der rhomboid major und der rhomboid minor. Zu den vorderen Muskeln gehören der Serratus anterior, der kleine Brustmuskel und der Subclavius.

Trapezmuskel

Der Trapezmuskel, „musculus trapezius“, oder wegen seiner Form und Position auch Kapuzenmuskel genannt, erstreckt sich vom Hinterhaupt (Hinterkopf) bis hin zum mittleren/unteren Rücken und bildet so mit dem Latissimus den Großteil der optischen Erscheinung des Rückens. Der Muskel entspringt, wie in der Skizze unten zu erkennen, am Schädel und der Wirbelsäule und verläuft hin zum Schulterblatt, dem Schulterdach und dem Schlüsselbein. Aufgrund der Größe und den unterschiedlichen Faserrichtungen des Muskels unterscheidet man zwischen drei Teilen mit jeweils anderen Faserrichtungen und entsprechend anderen Zugrichtungen (Umgangssprachlich „oberer,- mittlerer,- und unterer Trapez“ bezeichnet).

Pars descendens: Die kranial entspringenden Fasern verlaufen absteigend zu ihren Ansatzstellen.
Pars transversa: Die in der Mitte des Muskels entspringenden Fasern verlaufen in etwa horizontal.
Pars ascendens: Die am weitesten kaudal entspringenden Fasern verlaufen aufsteigend.

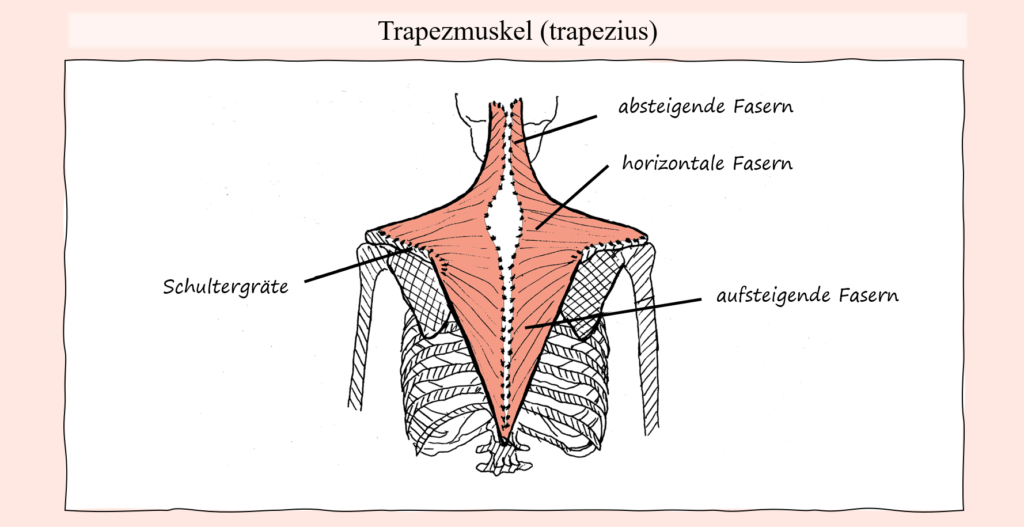
Die absteigenden Fasern verlaufen vom Schädel und den Dornfortsätzen der Halswirbel hin zum lateralen Drittel des Schlüsselbeins, wodurch sie die Schulter sowie das Schulterblatt nach oben ziehen. Die querverlaufenden Fasern entspringen an den 1. bis 4. Brustwirbeln und setzen am Acromion (Schulterdach) und der Schulterblattgräte an. Sie ziehen die Schulterblätter hinten zusammen. Die aufsteigenden Fasern verlaufen vom 12. bis 5. Brustwirbel nach oben in Richtung Schulterblatt, wo sie an der Schulterblattgräte ansetzten. Durch ihre Kontraktion ziehen sie das Schulterblatt nach unten- innen.

Alle drei Abschnitte ziehen also die Scapula nach medial (Richtung Wirbelsäule) und drehen sie nach außen. Zusätzlich hebt der absteigende Teil die Scapula und der aufsteigende Teil senkt sie, wodurch sich die Ausrichtung der Gelenkpfanne des Glenohumeralgelenkes, also des Schultergelenkes, ändert. Dadurch wird das Anheben der Arme über die Horizontale ermöglicht und die Scapula beim Tragen schwerer Lasten stabilisiert (siehe weiter unten eine bessere Darstellung der Schulterblattbewegung und der beteiligten Muskeln bei Aufwärts- und Abwärtsrotation). Eine einseitige Kontraktion der absteigenden Trapezius-Fasern führt zu einer Neigung des Kopfes (Lateralflexion) und einer Rotation des Kopfes. Eine beidseitige Kontraktion führt zu einer Hebung des Kopfes und Streckung der Halswirbelsäule (Dorsalflexion).

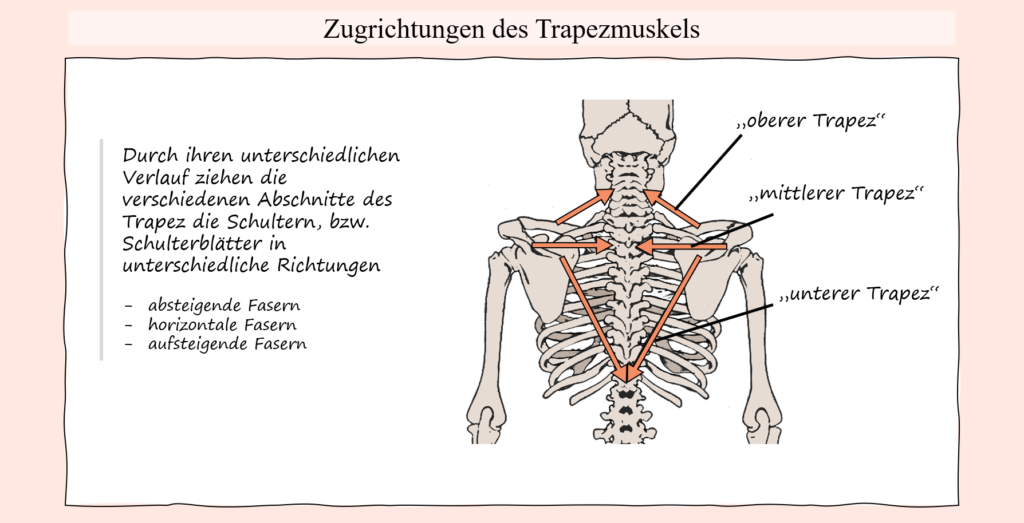
Rhomboiden

Die Rhomboiden, oder „musculi rhomboidei“ sind zwei beidseitige relativ kleine Muskeln im oberen Rückenbereich und werden ihrer Form wegen auch Rautenmuskel genannt. Die Rhomboiden liegen über der autochthonen Rückenmuskulatur (Rückenstrecker), weswegen sie zu den oberflächlichen Rückenmuskeln zählen, dennoch liegen sie unterhalb des Trapezius und werden von diesem verdeckt.

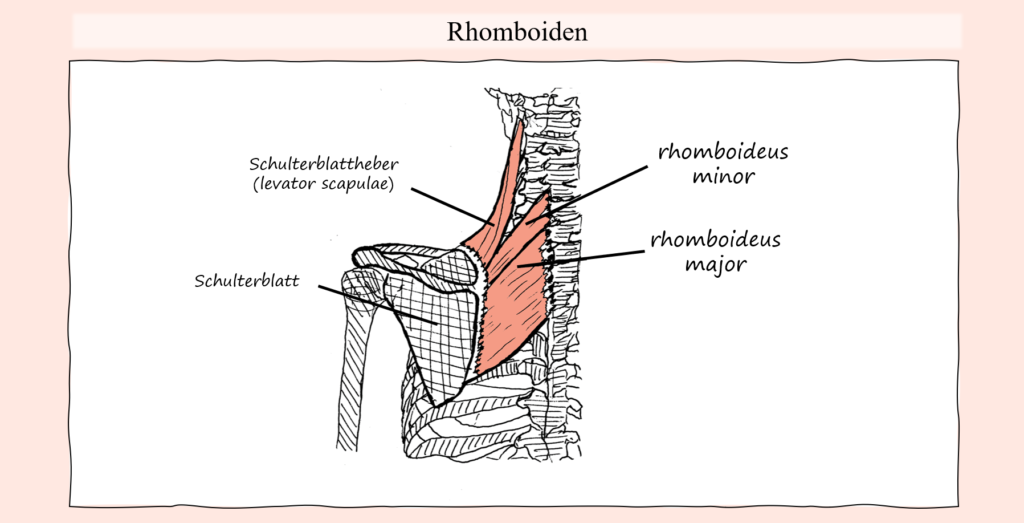
Sie bestehen aus zwei funktionell ähnlichen Muskeln

rhomboideus minor (kleiner Rautenmuskel) und
rhomboideus major (großer Rautenmuskel)

, wobei sich die Bewegungsfunktion nicht sonderlich unterscheidet. Der große „Rautenmuskel“ entspringt an den Dornfortsätzen vom 1. Bis 4./5. Brustwirbel und verläuft zur Innenkante des Schulterblattes unterhalb der Schulterblattgräte. Der rhomboideus minor hingegen entspringt an den letzten beiden, also den 6. und 7. Halswirbel und setzt an der Innenkante des Schulterblattes oberhalb der Schulterblattgräte an.

Da die Muskelfasern des Major und des Minor parallel verlaufen, üben sie eine sehr ähnliche bis gleiche Bewegungsfunktion aus. Das Schulterblatt wird nach kraniomedial (schräg nach Oben in Richtung Wirbelsäule) gezogen. Dabei wird gleichzeitig der Angulus inferior (die untere Spitze des Schulterblattes) der Scapula in Richtung der Wirbelsäule geführt, was also bei Abwärtsrotation des erhobenen Arms unterstützt. Ein weiterer Muskel, der in der Skizze oben zu erkennen ist, ist der Schulterblattheber. In seiner Funktion unterstützt er vor allem die oberen Fasern des Trapezmuskels, wobei er auch vollständig von diesem verdeckt wird. Er verläuft von den Querfortsätzen des 1. Bis 4. Halswirbels hin zum Schulterblatt an die „obere Ecke“ und zieht dieses entsprechend nach oben.

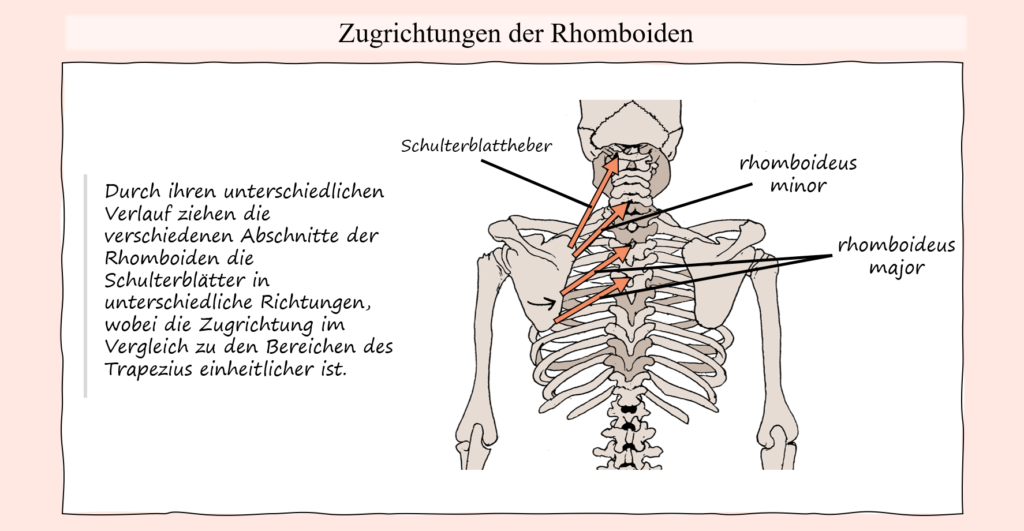
Serratus anterior

Der Serratus anterior ist ein breitflächiger Muskel an der seitlichen Thoraxwand, zu einem großen Teil unterhalb des Schulterblattes. Er entspringt an der 1. Bis 9. Rippe und setzt an der Vorderfläche der Innenkante des Schulterblattes an. Es wird zwischen drei Anteilen unterschieden:

den Pars superior – verläuft von der 1. Und 2. Rippe bis zum Angulus superior (obere innere Ecke) der Scapula
der Pars intermedia – verläuft von der 2.-3. Rippe bis zur Margo medialis (Innenkante) der Scapula
der Pars inferior – verläuft von der 4. bis 9. Rippe zur Margo medialis und dem Angulus inferior (die untere Spitze) der Scapula.

Seinem Verlauf entsprechend führt die Kontraktion des Serratus anterior zu einer ventrolateralen Verschiebung der Scapula entlang der Rippen. Durch den Zug des unteren Serratus anterior (Pars inferior) an der unteren Scapula kommt es zu einer Rotationsbewegung und damit zu einer Verschiebung des Schultergelenks nach oben (Aufwärtsrotation), was zum Anheben des Arms über 90° beiträgt. Der obere Anteil (pars superior) dagegen senkt die Schultergelenkpfanne, weil sein Zug an der oberen Kante zu einer gegensätzlichen Rotationsbewegung führt. Der Pars intermedia.

Bei fixierter Scapula hebt der Serratus anterior die Rippen und fungiert dadurch als Atemhilfsmuskel, wie seine Namensvetter der „serratus posterior superior“ und der „Musculus serratus posterior inferior“, welche zu den Atemmuskeln zählen.

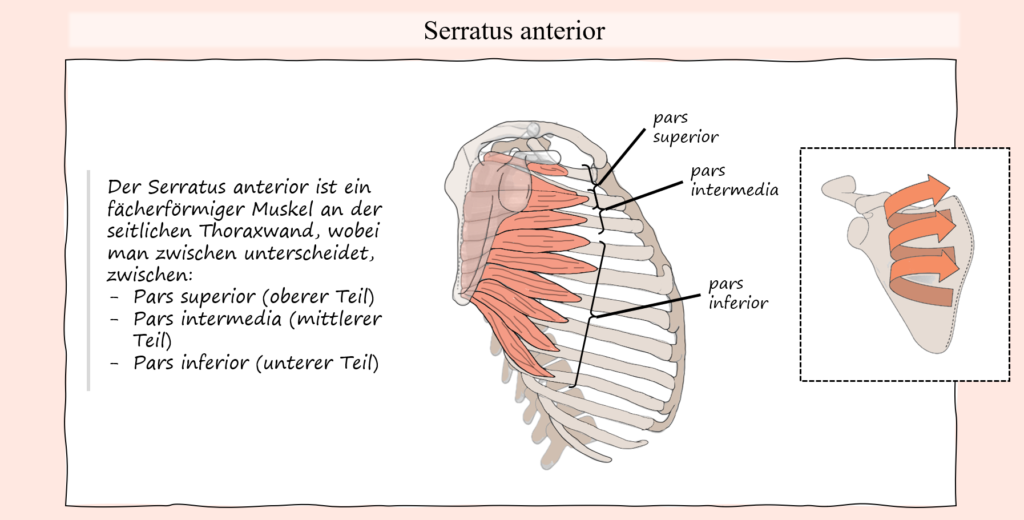
Pectoralis minor & Subclaviculus

Zu guter Letzt fehlen noch zwei kleinere Muskeln, welche den Schultergürtel aktiv stützen und positionieren, der kleine Brustmuskel, oder Pectoralis minor und der Subclaviculus.

Der „M. pectoralis minor“, sprich der kleine Brustmuskel liegt unterhalb des großen Brustmuskels und verläuft, dreiecksartig von der 3- 5 Rippe, hin zu einem Knochenfortsatz des Schulterblattes (Rabenschnabelfortsatz). Anders als der große Brustmuskel, welcher über das Schultergelenk zieht und damit den Oberarm bewegt, stabilisiert der kleine Brustmuskel das Schulterblatt und zieht dieses an den Brustkorb heran. Zum einen wird das Schulterblatt gesenkt und führt den Angulus inferior (die untere Spitze) wieder in Richtung der Wirbelsäule, was die Abwärtsrotation unterstützt.

Der subclavius Muskel verläuft seinem Namen entsprechend unterhalb des Schlüsselbeines. Es ist ein kleiner Muskel, welcher an der Knochen-Knorpel-Grenze der ersten Rippe entspringt und an der Unterseite der lateralen Clavicula ansetzt. Seine Funktion ist die aktive Stabilisierung des Schlüsselbeines, indem er dieses nach unten zieht.

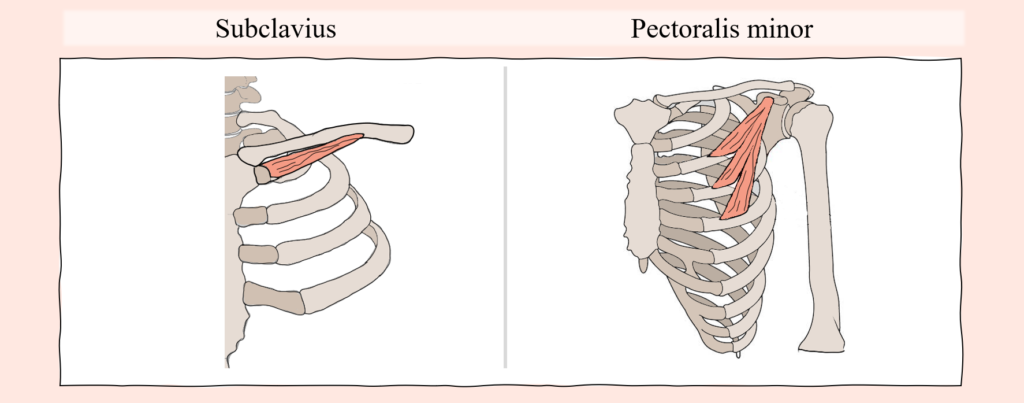
Position am Thorax	Bewegung	Ziel	Bewegungs-richtung (Zugrichtung)	Agonist	Ursprung	Ansatz
anterior	Stabilisiert die Clavicula durch Depression	Schlüsselbein	Depression	Subclavius	erste Rippe	Unterseite der lateralen Clavicula
anterior	Rotiert die Scapula nach anterior; unterstützt Atmung	Schulterblatt; Rippen	Schulterblatt: Depression; Rippen: Elevation	Pectoralis minor	Oberflächer der 3–5 Rippen	Raben-schnabelfortsatz der Scapula
anterior	Bewegt den Arm von der Seite des Körpers nach vorne; unterstützt Atmung	Schulterblatt; Rippen	Scapula: Protraktion; ribs: Elevation	Serratus anterior	Oberflächer der 1–9 Rippen	Anteriore Fläche des inneren Randes des Schulterblatts
posterior	Hebt Schultern; zieht Schulterblätter zusammen; neigt den Kopf	Schulterblatt; Hals-wirbelsäule	Scapula: Rotation, retraction, Elevation, Depression; Wirbelsäule: Extension	Trapezius	Schädel; Hals-wirbelsäule	Acromion, Schultergräte, Schlüsselbein
posterior	Stabilisirt Schulterblätter, zieht Schulterblätter zusammen, rotiert Schulterblätter	Schulterblatt	Retraktion; Rotation	Rhomboid major/minor	Hals (6,7)- und Brustwirbel (1-5)	Innenkante des Schulterblatts

Der Schultergürtel wird also von den Schlüsselbeinen sowie Schulterblättern gebildet. Muskeln, welche die Position und Ausrichtung des Schultergürtels bestimmen, haben eine zentrale Funktion für die Bewegung der oberen Extremität, weil das Schulterblatt die Gelenkpfanne bildet, in dem der Oberarmkopf geführt wird. Im Folgenden sind also nochmals speziell die Bewegungen des Schulterblatts, zuständige Muskeln samt einer Darstellung der Aufwärts- und Abwärtsrotation angeführt.

Bewegung	Beteiligte Muskulatur
Elevation	Pars descendens m. trapezii, M. levator scapulae, M.rhomboideus, Pars sup. M. serrati anterioris
Depression	Pars ascendens m. trapezii , Pars inferior m. serratianterioris, M. pectoralis minor
Protraktion	M. serratus anterior (oberer + mittlerer Anteil), M.pectoralis minor
Retraktion	Pars transversa m. trapezii, M. rhomboideus
Aufwärtsrotation (Elevation Armes)	Pars inf. m. serrati anterioris, partes descendens und ascendens m. trapezii
Abwärtsotation (Retroversion Arm)	Mm. Rhomboidei, M. pectoralis minor, M. levator scapulae, Pars superior m. serrati anterioris

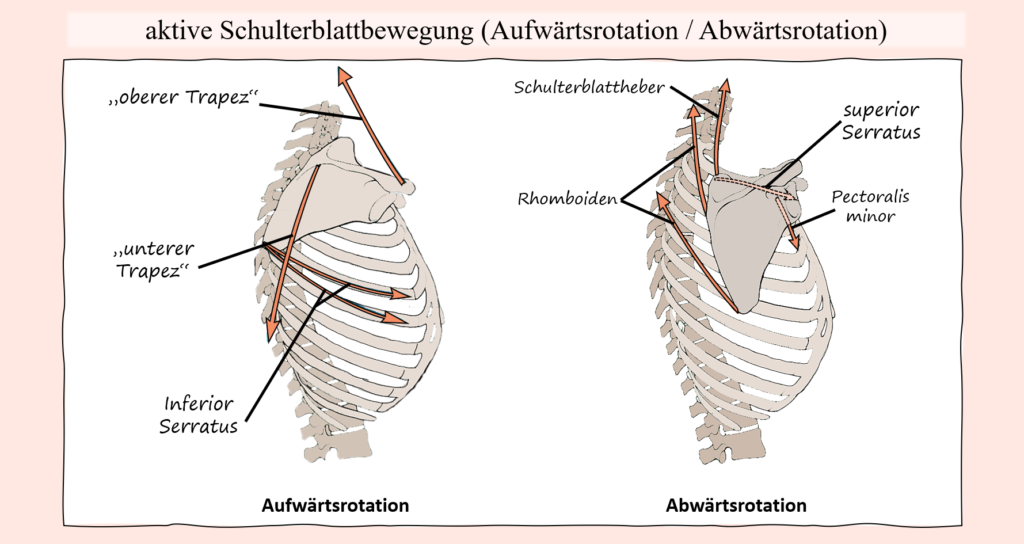
Muskeln, die den Humerus bewegen

Wie auch die Muskeln, die den Schultergürtel positionieren, können auch die Muskeln, die das Schultergelenk kreuzen und damit den Oberarmknochen des Arms bewegen, je nach Position bzw. Ursprung in zwei grobe Kategorien unterteilt werden, die Axial- als auch die Schulterblattmuskulatur. Axialmuskeln entspringen am Achsenskelett. Die beiden axialen Schultermuskeln (Muskeln, die über das Schultergelenk den Oberarm bewegen) sind der große Brustmuskel – pectoralis major – als auch der große Rückenmuskel – latissimus dorsi. Der Rest der Schultermuskulatur hat ihren Ursprung am Schultergürtel. Dieser bildet eine Basis, von der aus der Oberarmkopf in seinem Kugelgelenk mit der Gelenkpfanne des Schulterblatts den Arm in mehrere Richtungen bewegen kann, indem das Gelenk von zahlreiche Muskeln ringsum überzogen wird. Die anatomische und ligamentäre Struktur des Schultergelenks und die Anordnung der Muskeln, die es bedecken, ermöglichen es dem Arm, verschiedene Arten von Bewegungen auszuführen.

Pectoralis major

Der große Brustmuskel, oder „Musculus pectoralis major“, ist ein großer, fächerförmiger Muskel des Schultergelenks. Er erstreckt sich über den Großteil des Brustkorbes und verleiht ihn dessen typische Form. Die Brustmuskulatur an sich unterteilt man in zwei separate Muskeln, den „großen“- und „kleinen“ Brustmuskel, oder aber pectoralis major sowie pectoralis minor. Letzterer wurde ja samt seiner Rolle für die Positionierung und Stabilisierung des Schultergürtels bereits aufgegriffen. Der oberflächlich erkennbare Brustmuskel spiegelt jedoch nur den pectoralis major wider, weil der kleine pectoralis minor von ihm verdeckt wird.

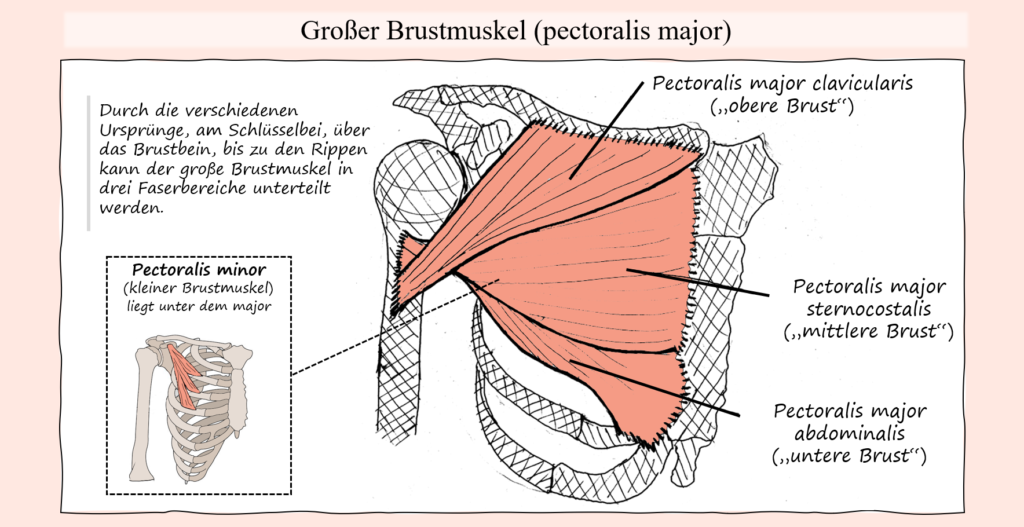
Je nach Ursprung und Faserrichtung lässt sich der große Brustmuskel in drei Teile unterteilen:

pars clavicularis,
pars sternocostalis
pars abdominalis.

Allgemeinsprachlich bezeichnet man diese auch schlichtweg als „obere“- „mittlere“- sowie „untere“- Brust. Der obere Teil hat seinen Ursprung an der medialen Hälfte des Schlüsselbeines (Clavicula), der mittlere Teil entspringt an der Außenseite des Sternums (Brustbein) sowie dem 2. Bis 6. Rippenknorpel und der untere Anteil am vorderen Blatt der Rektusscheide (Bauchmuskelhülle). Alle Teile verlaufen in Richtung Achsel zusammen, wo sie am proximalen Humerusschaft ansetzen. Wegen des sehr unterschiedlichen Verlaufs der Muskelfasern liegt am Ansatz, wie in der Skizze unten zu erkennen, eine Überlappung der Fasern vor.

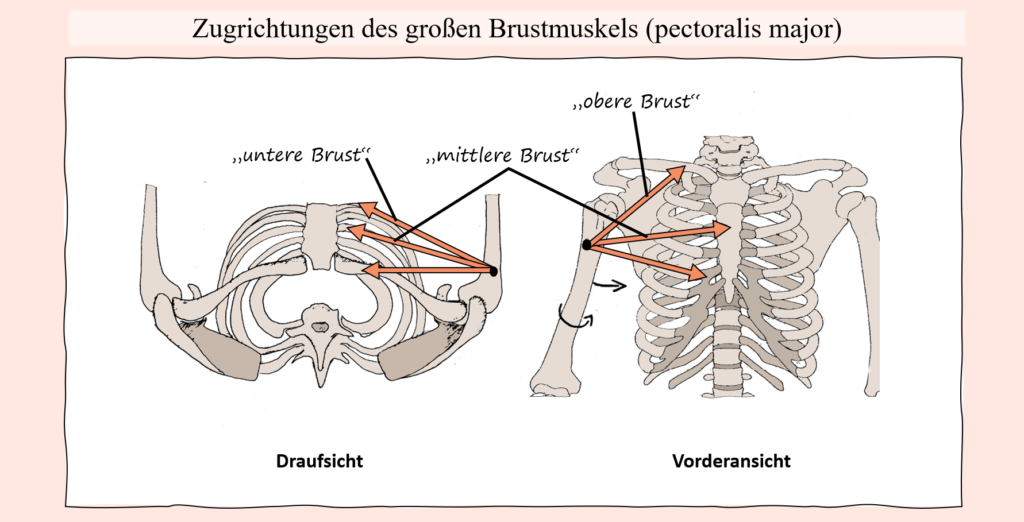
Seinen Verlauf entsprechend zieht der große Brustmuskel, „pectoralis major“, den Arm an den Körper heran und dreht in leicht nach innen (Innenrotation), wegen des Ansatzes am vorderen Teil des Knochens. Damit ist der pectoralis major der wichtigste Muskel für die Adduktion des Schultergelenks, aber auch für die Anteversion (Anheben des Arms nach vorne, also Flexion im Schultergelenk) ist der große Brustmuskel wichtig. Den unterschiedlichen Faserverläufen entsprechend ziehen die verschiedenen Abschnitte des Muskels den Oberarm in ihre jeweilige Richtung.

Latissimus dorsi

Der Latissimus, oder „M. latissimus dorsi“ ist der flächenmäßig größte Muskel des menschlichen Körpers und bedeckt an der dorsalen (hinteren) Rumpfwand den Großteil des Rückens, dafür ist er aber vergleichsweise dünn.

Gemäß seiner großen Fläche ist auch der Ursprung des Muskels sehr weiträumig und erstreckt sich über die Dornfortsätze der Brustwirbel 7 bis 12 und der Lendenwirbel 1 bis 5, das Kreuzbein, die Fascia thoracolumbalis, die 9. bis 12. Rippe und dem Beckenkamm, des Darmbeins. Daraus geht eine Unterteilung in drei Abschnitte hervor

pars vertebralis (Wirbelsäulenteil)
pars costalis (Rippenanteil)
pars iliaca (Darmbeinanteil).

Zum Ansatz hin verlaufen alle Fasern zusammen, hin zum oberen/ vorderen Teil des Oberarmknochens, wo sie zwischen pectoralis major und teres major (siehe unten) ansetzen.

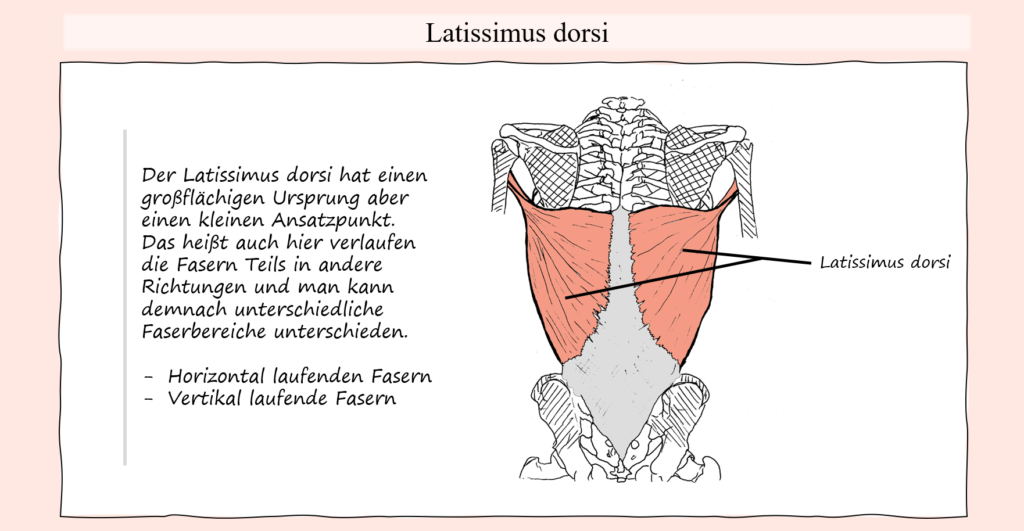
Die Funktionen des latissimus dorsi umfassen die Adduktion, Extension und Innenrotation des Armes, zudem unterstützt er die Retroversion.

Durch den medialen Ursprung und dem Ansatz am Oberarmknochen adduktiert der Latissimus den Arm, zieht ihn also an den Körper heran und führt den nach vorne angehobenem Arm zurück. Durch den Ansatz auf der Vorderseite des Knochens wird der Arm zusätzlich nach innen rotiert. Im Umkehrschluss zieht der Latissimus bei fixiertem Arm den Oberkörper an den Arm heran.

Auch wenn der Verlauf des Latissimus fächerartig ist, kann der Muskel aus funktioneller Sicht nach Faserverlauf – eher horizontal verlaufender Fasern sowie eher vertikal verlaufender Fasern – unterteilt werden.

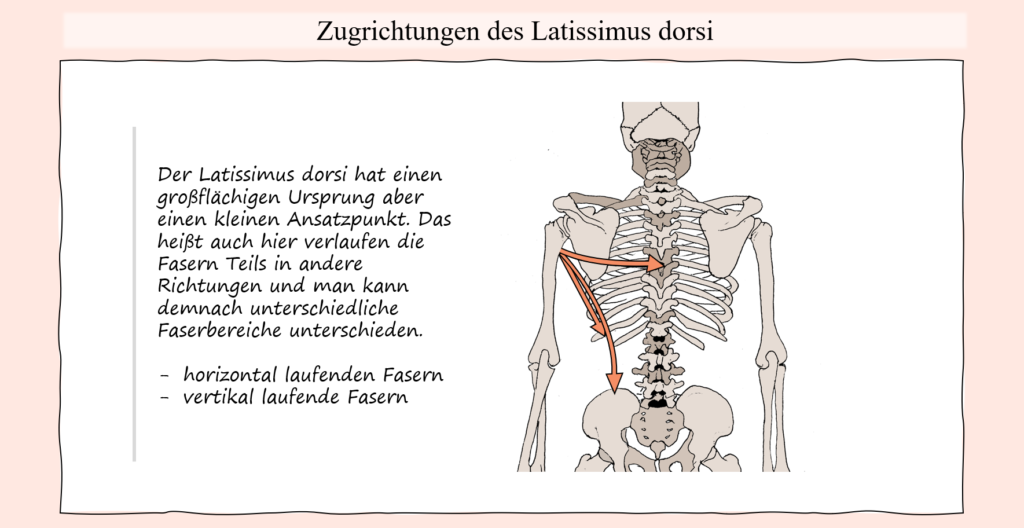
Rotatorenmanschette

Das Schultergelenk (Glenohumeralgelenk) wird nur von wenig knöchernen Strukturen gehalten, was überhaupt erst der Grund für den großen Bewegungsradius des Gelenkes ist. Andererseits büßt das Gelenk hierdurch natürlich an Halt und Stabilität ein. Die Hauptunterstützung für das Schultergelenk erfolgt durch die Muskeln, die das Gelenk überziehen, insbesondere durch die vier Muskeln der Rotatorenmanschette. Diese Muskeln (Supraspinatus, Infraspinatus, Teres Minor und Subscapularis) entspringen dem Schulterblatt und setzen nahe am Kopf des Oberarmknochens an. Die Sehnen jener Muskeln umschließen den Oberarmkopf und verschmelzen mit der vorderen, oberen und hinteren Wand der Gelenkkapsel. Die Verdickung der Kapsel, die durch die Verschmelzung dieser vier Muskelsehnen entsteht, wird Rotatorenmanschette genannt. Zusätzlich zu ihrer individuellen Funktion, die obere Extremität zu bewegen, dienen die Muskeln der Rotatorenmanschette also auch dazu, den Oberarmkopf in der Gelenkpfanne in Position zu halten, indem sie ihre Kontraktionsstärke ständig anpassen, um den auf die Schulter wirkenden Kräften standzuhalten.

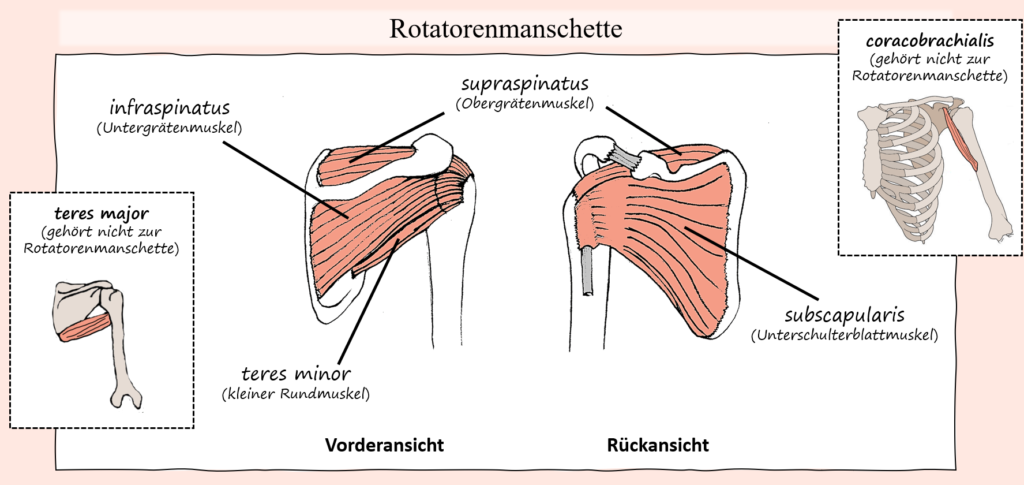
Die Muskeln der Rotatorenmanschette entspringen wie gesagt alle am Schulterblatt, wobei sie dieses fast vollständig abdecken.

Der Supraspinatus (Obergrätenmuskel) legt sich über das Schulterblatt, verläuft unter dem Schulterdach hindurch und setzt dann am Oberarmkopf an. Dieser Muskel ist, wie auch die „seitlichen“ Deltafasern beim seitlichen Anheben des Armes beteiligt.

Der Subscapularis (Unterschulterblattmuskel) ist der einzige Muskel der Rotatorenmanschette, der auf der Vorderseite des Schulterblattes entspringt. Dabei deckt er dieses größtenteils ab und zieht den Arm an den Körper heran, bzw. rotiert den Arm nach innen.

Der Infraspinatus (Untergrätenmuskel) verläuft unterhalb der Schulterblattgräte hin zum Oberarmkopf, ähnlich wie der teres minor (kleiner Rundmuskel), welcher unterhalb des infraspinatus verläuft und ansetzt. Sie adduktieren den Arm und, durch den Zug von hinten sind sie bei der Außenrotation des Armes beteiligt.

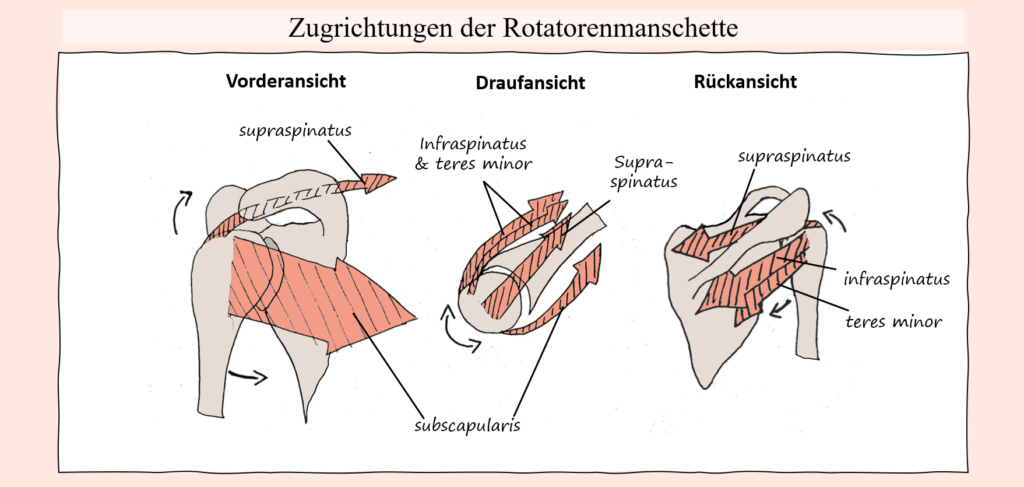
Grundsätzlich sind die Muskeln der Rotatorenmanschette also vor allem bei Innenrotation und Außenrotation des Armes beteiligt, sorgen aber natürlich auch für Halt im Gelenk und sind bei jeder Schulterbewegung beteiligt.

Innenrotation (und Adduktion): Subscapularis
Außenrotation (und Adduktion): Infraspinatus, Teres minor und
Abduktion: Supraspinatus

Der dicke und flache Teres Major verläuft unterhalb des Teres Minor, gehört aber nicht der Rotatorenmanschette an. Auch er zieht den Arm an den Körper (Adduktion), unterstützt aber die Innenrotation, durch seinen Ansatz an der Vorderseite des Humerus.

Und schließlich der coracobrachialis, welcher auch nicht zur Rotatorenmanschette gehört, aber der nur kurzen Erwähnung wegen hier untergebracht ist, verläuft auf der Vorderseite der Schulter vom Rabenschnabelfortsatz hin zur medialen Fläche des Humerusschafts wo er zwischen dem Brachialis und dem medialen Trizepskopf ansetzt. Er ist beteiligt bei der Adduktion und Schulter-Flexion.

Deltoid

Der Deltoid-Muskel, oder „musculus deltoideus“ (oder auch „Deltamuskel“), ist jener Muskel, welcher umgangssprachlich schlichtweg als Schultermuskulatur benannt wird. Grund hierfür ist sicherlich, dass er das Oberflächenrelief der Schulter maßgeblich prägt, ihr also ihre typische Form gibt.

Den Deltamuskel unterteilt man in drei Teile mit entsprechend anderem Ursprung bzw. Faserverlauf, wobei alle am mittleren, äußeren Oberarmknochen mit derselben Sehne ansetzen. Die Ursprünge der Fasern sind dabei aber sehr verschieden und verlaufen um das ganze Schultergelenk herum.

Pars clavicularis: Ursprung am lateralen Drittel des Schlüsselbeines
Pars acromialis: Ursprung am Acromion (Schulterdach)
Pars spinalis: Ursprung an der Schulterblattgräte

Umgangssprachlich spricht man dabei auch einfach von „vorderer“,- „seitlicher“,- und „hinterer“- sowie Schulter.

Gemeinsam setzen alle Anteile lateral an der anterioren lateralen Seite des Humerusschaftes an, wodurch der Muskel seine dreieckige Form erhält (wenn man ihn ausbreiten würde).

Die Bewegungen variieren je nach Muskelanteil und Lage des Oberarmknochens, sodass sie synergistisch, aber teilweise auch antagonistisch wirken können.

Der vordere Anteil der Schulter entspringt am äußeren Teil des Schlüsselbeins und dreht den Arm einwärts (Innenrotation), zieht den Oberarm in Richtung der Fasern, also in etwa in Richtung Kopf (Anheben des Armen – Anteversion), trägt unterhalb von etwa 60° zur Adduktion und oberhalb hingegen zur Abduktion bei. Der seitliche Teil entspringt am Schulterdach und abduziert den Oberarm, hebt den Arm also seitlich an. Der hintere Teil entspringt am Schulterblatt, genauer gesagt entlang der Schulterblattgräte, sorgt entsprechend für eine Bewegung des Arms nach hinten (Retroversion), durch den Ansatz am seitlichen, vorderen Oberarm wird der Oberarm auch nach außen rotiert (Außenrotation) und ebenso wie bei der vorderen Schulter wird unterhalb von 60° die Adduktion und oberhalb die Abduktion unterstützt.

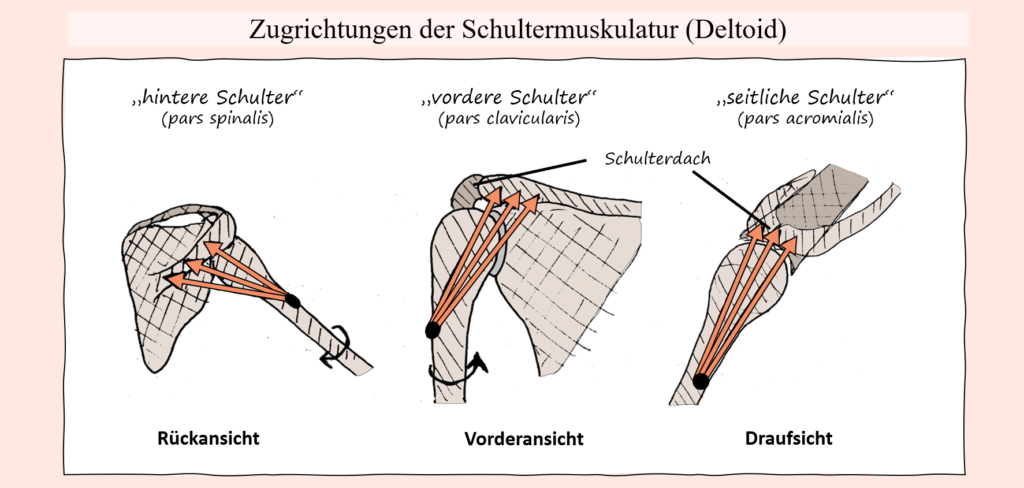
Bewegung	Ziel	Bewegungs-richtung (Zugrichtung)	Agonist	Ursprung	Ansatz
Axiale Muskeln
Bringt Oberarm zum Körper, Ellbogen zusammen und hebt den Arm nach vorne an	Humerus	Flexion; Adduktion; Innenrotation	Pectoralis Major	Schlüsselbein, Brustbein, Apponeurose der Bauchwand	Proximaler vorderer Humerusschaft
Zieht den Arm hinter den Körper, bringt Ellbogen nahe zum Körper	Humerus; Scapula	Humerus: Extension; Adduktion, Innenrotation Scapula: Depression	Latissimus dorsi	Brustwirbelsäule, Lendenwirbelsäule, unterer Rippen, Beckenkamm	Proximaler, vorderer Humerusschaft (zwischen Teres major und Pectoralis major
Scapulare Muskeln
Hebt den Arm nach vorne, seitlich und zieht in zurück	Humerus	Abduktion, Adduktion, Felxion, Extension, Rotation	Deltoid	Schlüsselbein, Schulterdach, Schulterblattgräte	anteriore laterale Seite des Humerusschaftes
Unterstützt Brust beim Zusammenführen der Ellbogen und rotiert den Arm nach innen	Humerus	Innenrotation	Subscapularis	Vordere Schulterblattfläche	vorderer Oberarmkopf
Rotiert den Oberarm nach außen	Humerus	Abduktion	Subraspinatus	Oberhalb der Schulterblattgräte	Lateraler Oberarmkopf
Rotiert den Oberarm nach außen	Humerus	Außenrotation; Extension; Adduktion	Infraspinatus	Unterhalb der Schulterblattgräte	Hinterer Oberarmkopf
Rotiert den Oberarm nach außen	Humerus	Außenrotation; Extension; Adduktion	Teres minor	seitlichen (lateraler) Rand des Schulterblattes	Hinterer Oberarmkopf
Rotiert den Oberarm nach innen und zieht den Arm an	Humerus	Außenrotation; Extension; Adduktion	Teres major	Angulus inferior	Proximaler, vorderer Humerusschaft
Hebt Arm schräg nach oben an	Humerus	Flexion; Adduktion	Coracobrachialis	Rabenschnabel-fortsatz	Medialer Humerusschaft

Muskeln, die den Unterarm bewegen

Der Unterarm, der aus den Knochen Speiche und Elle besteht, hat im Scharnier des Ellenbogengelenks vier Hauptwirkungsarten: Flexion (Beugung), Extension (Streckung), Pronation und Supination (Drehen des Handgelenkes). Zu den Unterarmflexoren gehören der Bizeps brachii, der Brachialis und der Brachioradialis. Die Strecker sind der Trizeps brachii und der Anconeus. Die Pronatoren sind der Pronator teres und der Pronator quadratus, und für die Supination ist der Supinator zuständig.

Biceps brachii

Der wohl bekannteste Unterarmbeuger, womöglich sogar der bekannteste Muskel, der Bizeps, ist ein zweiköpfiger Muskel, der nicht nur über das Ellbogengelenk zieht, sondern auch das Schultergelenk. Der „musculus biceps brachii“ setzt sich aus zwei Köpfen zusammen:

Caput longum (langer Bizepskopf)
Caput breve (kurzer Bizepskopf)

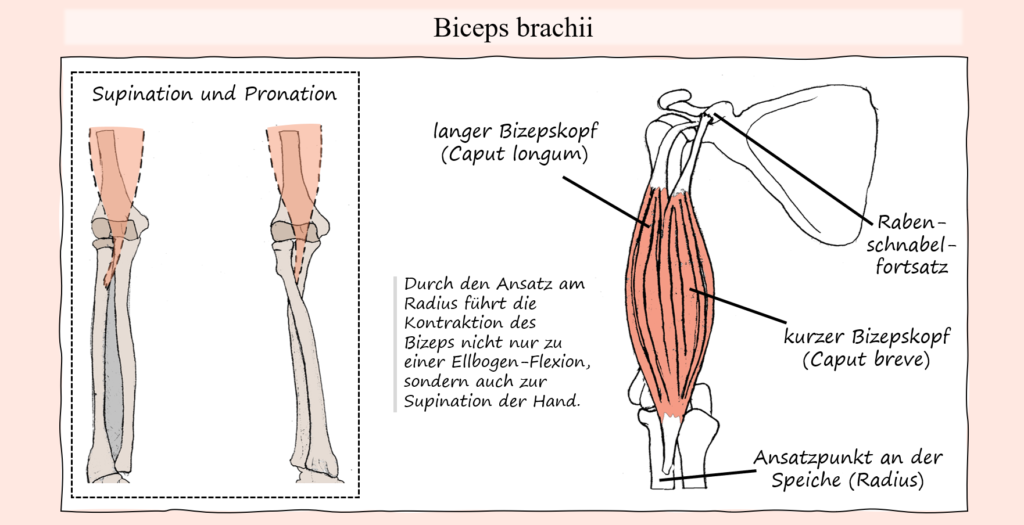
Der kurze Kopf entspringt am Rabenschnabelfortsatz wie auch der Coracobrachialis und der lange Kopf am Oberrand der Schulterpfanne (unterhalb des Schulterdachs, intrakapsulär, aber extrasynovial). Die Sehne des langen Bizepskopfes verläuft aufgrund einer Bandfixierung durch eine kleine Umlenkung am Oberarm entlang. Beide Köpfe verlaufen dann über den vorderen Oberarmknochen und das Ellbogengelenk, sie vereinen sich zu einem Muskel und setzten mit einer Sehne an der Speiche an. Die Teilung der Köpfe ist aufgrund des Schultermuskels, der den Bizeps teilweise überdeckt, von außen nicht sichtbar.

In seiner Funktion ist der biceps brachii vor allem für die Ellbogen-Flexion als auch die Supination der Hand verantwortlich (dreht den Unterarm so, dass die Handfläche wie in der Normalposition nach vorne, bzw. bei gebeugten Ellbogen nach oben zeigt). Die beiden Muskelköpfe führen dabei aber teilweise unterschiedliche Funktionen aus.

Der lange Kopf abduziert den Arm leicht (hebt vom Brustkorb ab), wohingegen der kurze Kopf ihn leicht adduziert (führt zum Brustkorb). Beide Köpfe unterstützen zusätzlich die Anteversion (Anheben des Armes nach vorne) sowie Innenrotation des Armes. Insgesamt ist der Bizeps zusammen mit dem Brachialis und Brachioradialis aber natürlich für die Ellbogen-Flexion hauptverantwortlich. Dabei ist die Flexionswirkung des Bizeps in Supinationsstellung am stärksten. In Pronationsstellung ist sie schwach. Hier überwiegt die Flexionswirkung des Brachioradialis und Brachialis. Das geht darauf zurück, dass sich die Speiche bei einer Pronation des Unterarmes um die Elle windet und somit der Ansatz der Bizepssehne ungünstig liegt. Andererseits trägt der Bizeps dadurch aber auch zur Supination bei, weil die gerade Ausrichtung der Zugrichtung des Bizeps gleichzeitig die Hand zu einem gewissen Grad supiniert. Die Supinationswirkung des Bizeps ist beim gebeugten Ellenbogen am kräftigsten, bei gestreckten Ellbogen geht die aktive Supination vor allem auf den Supinator zurück (siehe unten).

Brachialis

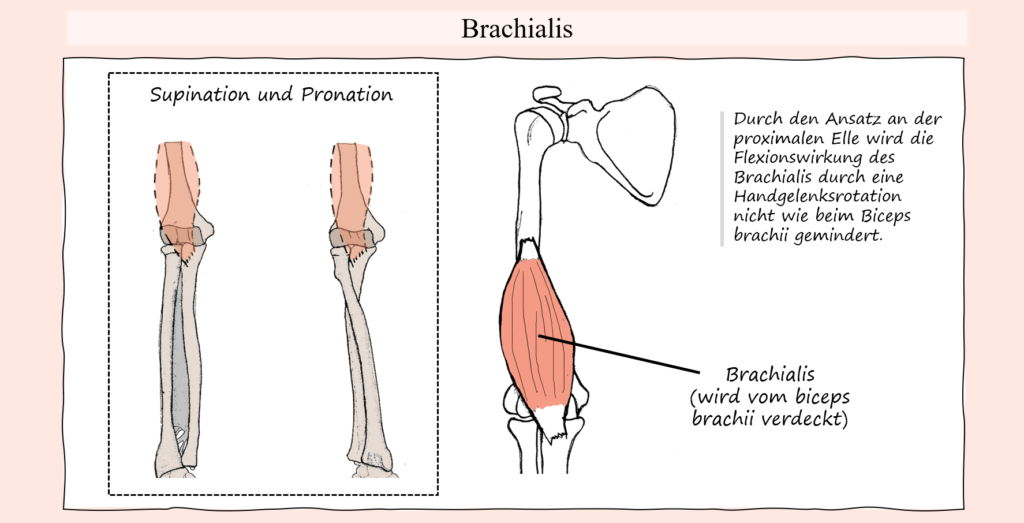
Der „musculus brachialis“ wird Großteils vom Bizeps verdeckt. Lediglich an seiner lateralen Grenze und distal liegt er teilweise oberflächlich. Trotzdem trägt er erheblich zum Oberflächenrelief des Oberarms bei, weil er den darüberliegenden Bizeps nach außen drückt und größer erscheinen lässt. Der Brachialis entspringt an der distalen Hälfte der vorderen Fläche des Humerus und verläuft über das Ellbogengelenk, wo er dann an der Elle (Ulna) ansetzt.

Dem Verlauf entsprechend liegt seine Funktion in der Flexion des Ellbogengelenkes. Im Gegensatz zum Bizeps zieht der Brachialis aber nur über das Ellbogengelenk und hat auch bei proniertem Unterarm eine starke Flexionswirkung, weil sich die Elle und damit auch der Ansatzpunkt des Brachialis durch die Handgelenksrotation nicht verändert.

Brachioradialis

Der „musculus brachioradialis“, oder auch Oberarmspeichenmuskel, ist ein Teil der radialen Muskulatur des Unterarms, anders als die meisten anderen Unterarmmuskeln, welche die Hand und Finger kontrollieren, zieht der Brachioradialis gemäß seines Namens aber über das Ellbogengelenk (von Brachium zum Radius).

Er entspringt am distalen, seitlichen Rand des Humerus. Von hier aus zieht er auf der radialen Seite des Unterarms Richtung Hand und setzt lateral am distalen Radius (Speiche), kurz vor dem Handgelenk, an.

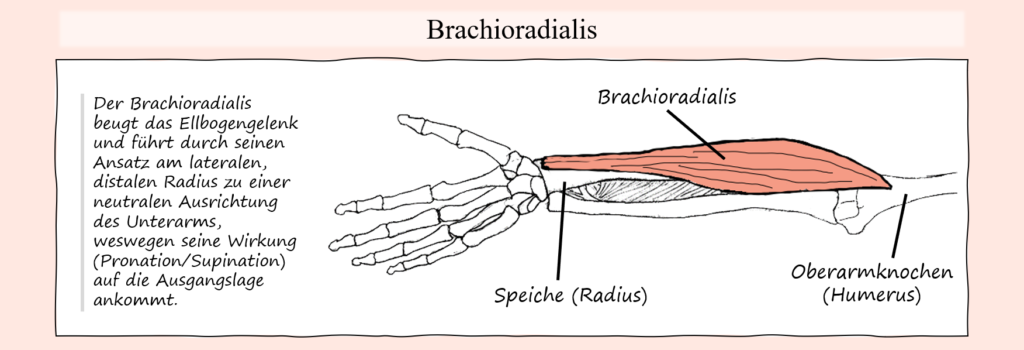
Der M. brachioradialis erfüllt drei Funktionen. Wie auch der Biceps brachii und der Brachialis gehört er zu den Ellbogen-Flexoren. Am Unterarm sorgt er für eine Neutralausrichtung der Hand (zwischen Pronation und Supination, also bei gebeugtem Ellbogen Daumen nach oben). Das wiederum bedeutet, dass er je nach Handgelenksposition zur Supination oder aber zur Pronation beitragen kann. Bei pronierter Hand wirkt er bis zur Neutralstellung als Supinator und bei supinierter Hand bis zur Neutralstellung als Pronator.

Triceps brachii

Der Trizeps liegt auf der dem Bizeps entgegengesetzten Seite des Oberarms. Sein Name, Trizeps, oder „M. triceps brachii“ geht darauf zurück, dass es ein dreiköpfiger Muskel ist. Das bedeutet, er setzt sich aus drei Köpfen mit entsprechend anderem Ursprung zusammen.

caput lateralis (kurzer Trizepskopf)
caput mediale (mittlerer Trizeps-Kopf)
caput longum (langer Trizeps-Kopf)

Der „lange Kopf“ entspringt als einziger am Schulterblatt, wohingegen der „kurze Kopf“ als auch der „mittlere Kopf“ am dorsalen Humerus entspringen. Der mediale Kopf wird Großteils von den beiden anderen Teilen verdeckt. Hin zum Ellbogen verlaufen alle drei in dieselbe Sehne und setzen am Ellenhacken an.

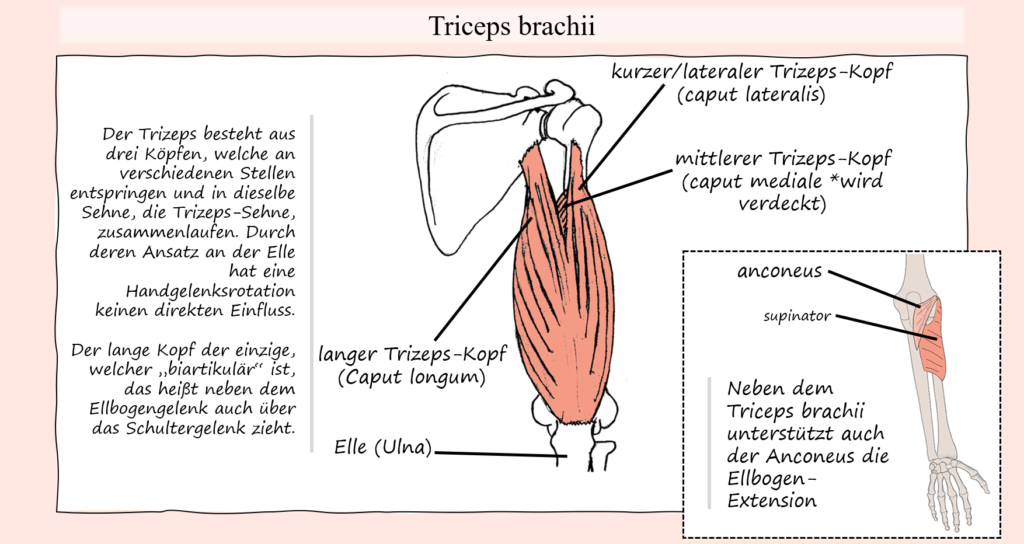
Der Trizeps ist der wichtigste Extensor, also Streckmuskel des Ellenbogens. Dadurch, dass bei einer Rotation der Hand lediglich die Speiche um die Elle gewunden wird, die Position der Elle durch eine Rotation aber nicht verändert wird, hat auch dies keinen direkten Einfluss auf den Trizeps.

Im Gegensatz zu den beiden anderen Köpfen zieht der lange Trizepskopf ebenfalls über das Schultergelenk und ist daher zweigelenkig. Dort zieht er den Oberarm zum Rumpf (Adduktion) und nach hinten (Retroversion).

Der Trizeps ist aber nicht der einzige, wenn auch der wichtigste, Ellbogenstrecker. Ein kleiner dreieckiger Muskel, der „musculus anconeus“, am Ellbogen erfüllt funktionell nämlich die gleichen Aufgaben wie der Trizeps, er unterstützt die Extension, also Streckung des Ellbogens und stützt den Ellbogen.

Pronatoren und Supinatoren

Pronatoren und Supinatoren sind Muskeln, welche das Handgelenk rotieren, oder besser gesagt supinieren und oder pronieren. Pronation und Supination des Handgelenks basiert auf Bewegungen der Speiche. In supinierter Stellung, wie in der anatomischen Normalposition, liegen die beiden Unterarmknochen parallel, in pronierter Stellung überkreuzen sie sich. Pronatoren und Supinatoren sind also Muskeln, welche die Ausrichtung der Unterarmknochen kontrollieren, indem sie vor allem die Speiche (Radius) entweder in supinations- oder pronations-Richtung ziehen.

Der Pronator teres ist ein zweiköpfiger Muskel auf der ventralen Seite des Unterarms und gehört zu den Flexoren sowie natürlich den Pronatoren des Unterarms. Er entspringt an der distalen, medialen Seite des Humerus und läuft von proximal-medial nach distal-lateral, also schräg über den Unterarm und setzt am mittleren Drittel des Radius (Speiche) an. Aufgrund seines Ursprungs am distalen Humerus und seines Ansatzes am Radius, wodurch er über das Humeroulnargelenk (Ellbogengelenk) zieht, kann der Pronator teres eine schwache Flexionsbewegung im Ellenbogengelenk durchführen. Seine Hauptfunktion liegt jedoch in der Pronation des Unterarms (im Radioulnargelenk), indem er den Radius durch seine Kontraktion über die Elle wendet und damit die Hand proniert.

Der Pronator quadratus ist ein quadratischer Pronator-Muskel am distalen Unterarm. Er entspringt flächig an der distalen Ulna (Elle) und setzt ebenfalls flächig am distalen Radius an. Die Funktion des Muskels ist dem Namen entsprechend natürlich die Pronation. Zusammen sind der Pronator teres und quadratus die wichtigsten Pronatoren des Unterarms.

Der musculus supinator bewirkt, wie der Name schon verrät, eine Supination des Unterarms. Er entspringt mitunter an der lateralen Seite des Humerus, gleich neben dem distalen Gelenkkopf und setzt an der lateralen, anterioren Seite des proximalen Drittels des Radius an. Durch seine Kontraktion zieht er den Radius in die supinierte Stellung nach lateral und wendet damit die Hand.

Bewegung	Ziel	Bewegungs-richtung (Zugrichtung)	Agonist	Ursprung	Ansatz
anteriore Muskeln
beugt den Ellbogen, supiniert die Hand, hebt den Arm leicht an	Unterarm; Oberarm	Flexion; Supination	Biceps brachii	Rabenschnabel-fortsatz; Oberrand der Schulterpfanne	proximaler Radius
Beugt den Ellbogen	Unterarm	Flexion	Brachialis	distale Hälfte der anterioren Humerus-Fläche	proximale Elle
beugt den Ellbogen und richtet die Hand neutral aus		Flexion; Neutralstellung	Brachioradialis	distaler – lateraler Rand des Humerus	lateral am distalen Radius
posteriore Muskeln
streckt den Ellbogen und führt den Arm leicht nach hinten	Unterarm; Oberarm	Extension	Triceps brachii	proximaler Oberarm; laterales Schulterblatt	Ellenhacken
Streckt den Ellbogen	Unterarm	Extension	anconeus	distaler Oberarm	Anteriore proximale Elle
Anteriore Muskeln (Pronation)
proniert die Hand	Unterarm	Pronation; Flexion	Pronator teres	distaler – medialer Humerus	mittleren Drittel Radius
proniert die Hand	Unterarm	Pronation	Pronator quadratus	distale Elle	distaler Radius
posteriore Muskeln (Supination)
supiniert die Hand	Unterarm	Supination	Supinator	lateraler – distaler Humerus	laterale anteriore Seite des proximalen Radius

Muskeln des Beckengürtels und der unteren Gliedmaßen

Der Beckengürtel dient als Grundlage für die unteren Gliedmaßen. Im Vergleich gibt es am Schultergürtel viel mehr Bewegung als am Beckengürtel, dessen Bewegung aufgrund seiner festen Verbindung mit dem Kreuzbein an der Basis des Achsenskeletts sehr gering ist. Dieser geringere Bewegungsspielraum geht andererseits aber mit mehr Stabilität einher, welche der Beckengürtel braucht, da er den Körper stabilisieren und stützen soll. In diesem Sinne spricht man hier auch nicht von Muskeln, die den Beckengürtel positionieren, wie im Falle des Schultergürtels, sondern vielmehr von Muskeln, welche am Becken ansetzen und je nach Ausgangslage den Oberschenkel und bei fixiertem Oberschenkel das Becken bewegen.

Die Muskulatur des Beckengürtels und der unteren Extremität lässt sich grob in drei Kategorien unterteilen:

Muskeln der Gesäßregion, die den Oberschenkel bewegen
Oberschenkelmuskeln, die Femur, Schienbein und Wadenbein bewegen
Muskeln, die die Füße bewegen

Jene Muskeln erfüllen diese Bewegungsfunktionen, indem sie über entsprechende Gelenke hinwegziehen, wobei das Hüftgelenk, das Kniegelenk und das Fußgelenk im Fokus stehen.

Becken und Hüftgelenk

Das Becken beschreibt den Abschnitt des Körpers zwischen Bauch und Beinen. Im skelettalen System bildet der Beckenknochen die Verbindung des axialen Skeletts mit der unteren Extremität. Der Beckenknochen selbst setzt sich zusammen aus dem linken und rechten Hüftbein und dem Kreuzbein. Die Hüftbeine wiederum setzten sich zusammen aus Darmbein, Sitzbein und Schambein. Zusammen bilden sie den Hüftgürtel, welcher wie auch der Schultergürtel, der die Verbindung der oberen Extremität bildet, durch die Hüftgelenke die bewegliche Verbindung des Oberschenkels mit dem Becken bildet. Beim Hüftgelenk handelt es sich um das zweitgrößte Gelenk im Körper und es ist ein Kugelgelenk, wobei der Gelenkkopf im Gegensatz zur Schulter in eine tiefe knöcherne Gelenkkapsel eingebettet ist. Die Pfanne wird von Anteilen des Darmbeins, Sitzbeins und Schambeins gebildet. So ist das Gelenk als Kugelgelenk zwar in drei Achsen bewegbar (Flexion-Extension, Adduktion-Abduktion, Innenrotation-Außenrotation), jedoch ist der Bewegungsraum im Gegensatz zur Schulter durch die knöcherne Pfanne, welche den Gelenkkopf bis über seinen Äquator hinaus umschließt, beschränkt und wird dadurch auch als sogenanntes „Nussgelenk“ bezeichnet. Gestützt wird das Hüftgelenk also vor allem durch die Pfanne, samt einer Gelenkknorpellippe, aber auch von einem Bandapparat, der sich um das ganze Gelenk legt.

Wie gesagt ist diese höhere Stabilität im Vergleich zur Schulter notwendig, das Becken trägt durch unseren aufrechten Gang, die Last des gesamten Oberkörpers, verteilt diese dann gleichmäßig auf die beiden Hüftgelenke und damit auf die Beine. Die Schulter hingegen ist hauptsächlich für Greifbewegungen des Armes zuständig, braucht dazu mehr Bewegungsspielraum, was durch die sehr kleine Gelenkpfanne und den beweglichen Schultergürtel erreicht wird. Würde der Beckengürtel zu einem Bewegungsausmaß in der Lage sein, wie die Schulter und die Köpfe der Oberschenkelknochen nicht in der Hüftpfanne des Beckens befestigt wären, dann würde das Gehen koordinativ deutlich anspruchsvoller sein und mehr Energie verbrauchen. Auch der Körperschwerpunkt liegt im Bereich des Beckens. Würde der Schwerpunkt nicht fixiert bleiben, wäre auch das Aufstehen schwierig. Was dem Beckengürtel und den Beinmuskeln also an Bewegungsfreiheit und Vielseitigkeit fehlt, machen sie durch Größe und Kraft wett und erleichtern die Stabilisierung, Haltung und Bewegung des Körpers.

Kniegelenk

Das Kniegelenk ist das größte Gelenk des menschlichen Körpers. Es verbindet den Oberschenkel mit dem Unterschenkel, genauer gesagt das Schienbein mit dem Oberschenkel sowie der Kniescheibe. Dabei unterscheidet man auch hier zwei Gelenke, zum einen das Oberschenkel-Schienbeingelenk (Femorotibialgelenk) und zum anderen das Oberschenkel-Kniescheibengelenk (Femoropatellargelenk).

Das große Kniegelenk erscheint funktionell gesehen zunächst wie ein klassisches Scharniergelenk, welches Flexion und Extension zulässt. In Wahrheit handelt es sich hierbei aber um ein sogenanntes „bicondyläres Gelenk“ oder auch Drehscharniergelenk oder Kondylengelenk genannt, was eine Art Mischung zwischen Drehgelenk und Scharniergelenk darstellt. Als Kondylengelenk ermöglicht das Knie wie das klassische Scharniergelenk eine Flexions- und Extensionsbewegung, aber zusätzlich noch die eingeschränkte Innen- und Außenrotation, welche aber nur in gebeugter Stellung möglich ist. Eine weitere Besonderheit des Kniegelenkes ist, dass die Gelenkflächen nicht perfekt ineinanderpassen. Deswegen sind zwischen den Gelenkflächen zwei Faserknorpelige Scheiben, die sogenannten Menisken, die die Kontaktfläche verbessern und gleichzeitig als „Dämpfer“ fungieren, indem sie einen Teil der Last aufnehmen und die Last gleichmäßig verteilen.

Wenn man sich das Knie ansieht, so wird man feststellen, dass dieses relativ frei liegt. Weder wird es von besonders vielen Muskeln umgeben und gehalten, wie zum Beispiel das Schultergelenk, noch wird es von Knochen umgeben wie das Hüftgelenk. Das Kniegelenk wird nämlich zum großen Teil durch Bänder stabilisiert. Die wichtigsten sind dabei die zwei Seitenbänder, sowie die beiden Kreuzbänder. Die Funktionsweise ist dabei ziemlich einfach. So sorgen die Seitenbänder dafür, dass sich der Oberschenkel und das Schienbein nicht seitlich verschieben oder aber das Knie seitlich aufklappt. Die Seitenbänder sind bei gestrecktem Knie gespannt und bei gebeugtem Knie lockerer. Und die Kreuzbänder sind vor allem dazu da, dass sich die Gelenkflächen nicht nach vorne oder hinten verschieben.

Was die Bewegung des Femorotibialgelenkes angeht, wurde ja bereits gesagt, dass es sich um ein Drehscharniergelenk handelt und demnach Extension-Flexion, aber euch eine leichte Innen- und Außenrotation möglich ist. Bei Flexion kommt eine kleine Besonderheit hinzu, nämlich drehen sich die Knochen nicht um eine fixe Achse, sondern in der Anfangsphase der Beugung, bis etwa 25°, rollen die Femurkondylen nach Dorsal ab, bei stärkerer Flexion drehen die Kondylen dann auf der Stelle, mit geringen Gleitbewegungen, sodass die Kontaktfläche der Femurkondylen bei Flexion im Vergleich zum gestreckten Knie an den dorsalen Rand des Tibiaplateaus bewegt werden. Was die Innen- und Außenrotation angeht, ist diese wie gesagt nur in gebeugter Stellung möglich. Grund hierfür sind vor allem die Bänder. Im gebeugten Gelenk sind die Seitenbänder nämlich entspannt.

Das zweite Gelenk am Knie ist die Verbindung von Oberschenkel und der Patella (Kniescheibe). Die Kniescheibe selbst ist ein kleiner flacher Sesamknochen, der in eine Sehne eingebettet ist. Diese Sehne ist die Ansatzsehne des Quadrizeps und läuft in die Patellasehne unterhalb der Kniescheibe über. Dadurch kann die Sehne mit einem für die Streckbewegung mechanisch günstigeren Winkel einstrahlen. Die Patella hat also zwei wesentliche Funktionen. Zum einen mindert sie Stöße sowie Reibung, weswegen die Rückseite eine dicke Knorpelschicht aufweist und sich hier auch mehrere Schleimbeutel („weiche Puffer“) befinden. Aber vor allem erhöht die Patella die Effizienz der Quadrizeps-Muskulatur, indem sie die Sehne weiter vom Drehpunkt entfernt und so der Hebel der Muskulatur auf das Gelenk erhöht wird.

Im Laufe einer Knieflexion gleitet die Patella parallel zu Beugung ihrem Gleitlager bis zu etwa 6 cm nach kaudal (fußwärts).

Fuß und Fußgelenk

Der Fuß ist im Grunde relativ ähnlich aufgebaut wie die Hand, was aus evolutionärer Perspektive natürlich nicht verwunderlich ist. Entsprechend unterscheidet man auch hier zwischen Fußwurzel, Mittelfuß sowie Zehen und einer Menge Gelenke, welche all diese Knochen verbinden. Das eigentliche „Fußgelenk“ beschreibt dabei das Sprunggelenk, oder besser gesagt, die Sprunggelenke. Denn auch hier werden im Grunde zwei Sprunggelenke beschrieben. Dabei gibt es das obere, als auch untere Sprunggelenk. Das obere verbindet das Sprungbein mit dem Schienbein. Das untere hingegen verbindet drei Knochen, das Sprungbein, das Fersenbein und das Kahnbein.

Wie auch bei der Hand, lässt sich auch der Fuß in Summe sehr vielfältig bewegen, isoliert betrachtet sind die Sprunggelenke allein aber gar nicht so beweglich. Das obere Sprunggelenk ist ein Scharniergelenk und ermöglicht die auf- und ab-Bewegung des Fußes (Dorsalflexion und Plantarflexion). Beim unteren Sprunggelenk handelt es sich funktionell am ehesten um eine Art Radgelenk mit einer Bewegungsachse. Das untere Sprunggelenk ermöglicht die Inversion (Drehung des Rückfußes nach medial) und Eversion (Drehung des Rückfußes nach lateral), also die „Neigung“ des Fußes nach links und rechts. Morphologisch handelt es sich dabei also um zwei getrennte Gelenke. Sie sind jedoch aus funktioneller Sicht so eng miteinander verknüpft, dass sie als Komplex betrachtet werden müssen.

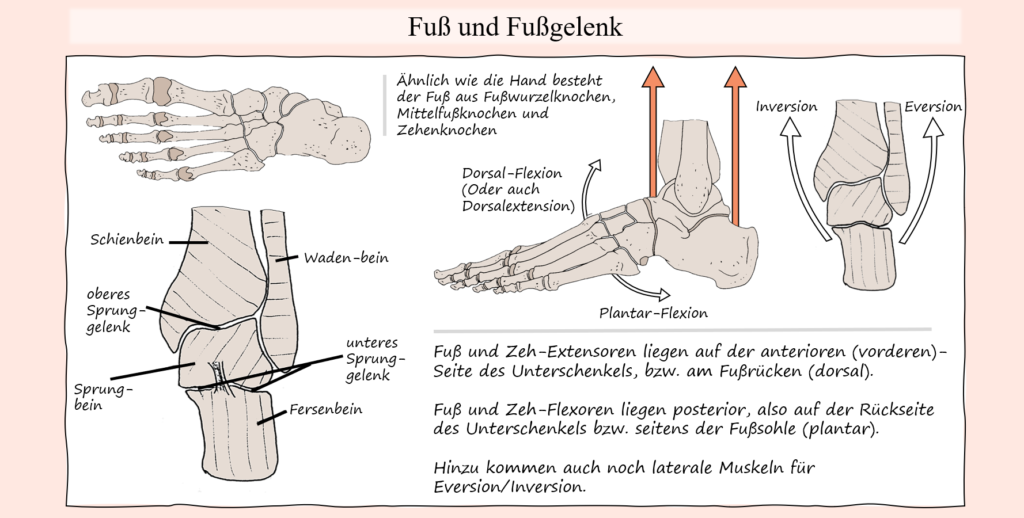
Muskeln des Oberschenkels

Der Oberschenkel ist ringsum von Muskeln umgeben, die einerseits über die Hüfte und andererseits über die Knie ziehen, oder natürlich beide. In diesem Sinne können wir die Muskulatur des Oberschenkels grob in drei Kategorien einteilen. Zum einen Muskeln der Gesäßregion, welche am Oberschenkel ansetzen und damit das Hüftgelenk kontrollieren, Muskeln des Oberschenkels, welche vor allem über das Knie den Unterschenkel bewegen, aber auch zum Teil über die Hüfte ziehen und abschließend Muskeln, die die Füße bewegen, wobei wir uns hier auf einige wenige ausgewählte Muskeln beschränken werden.

Muskeln der Gesäßregion, die den Femur bewegen

Zu den Muskeln der Gesäßregion, die den Femur bewegen, also über das Hüftgelenk hinwegziehen, gehören die Gruppe der Gesäßmuskeln, also Gluteus maximus / medius / minumus, die Gruppe der Adduktoren, sowie die Hüftbeuger und die Gruppe der Außenrotatoren.

Gluteus medius/minimus

Die Muskeln „musculus gluteus medius“ und „musculus gluteus minimus“ sind Teil der dorsolateralen Gesäßmuskulatur und werden dementsprechend auch als die „kleinen Gesäßmuskeln“ bezeichnet. Der Gluteus minimus liegt mitsamt den Rotatoren tief und wird fast vollständig vom Gluteus medius verdeckt.

Die beiden Muskeln unterscheiden sich hauptsächlich in ihrer Größe, wobei der Verlauf relativ ähnlich ist. Beide entspringen an der glutealen Seite der Darmbeinschaufel, wobei der Gluteus medius weiter kranial (also weiter oben) entspringt und so den Minimus überdeckt. Ihr Ansatzpunkt ist am Oberschenkel, genauer gesagt der große Rollhügel (Trochanter major), der für den Femur charakteristische große Knochenvorsprung, wobei der Gluteus minimus etwas weiter ventral (vorne) und der Gluteus medius seitlicher ansetzt. Dem sehr ähnlichen Verlauf entsprechend bilden die beiden kleinen Gesäßmuskeln auch eine funktionelle Einheit. Ihre wichtigste Aufgabe ist die Stabilisation der Hüfte. So sind sie dafür verantwortlich, dass beim Gehen oder Stehen auf einem Bein die Hüfte nicht auf die Seite des erhobenen Beines abknickt. Aber das ist nicht alles, zusammen können der Gluteus minimus und die ventralen Anteile des Gluteus Medius im Hüftgelenk eine Innenrotation und Flexion bewirken, wohingegen die dorsalen Anteile die Außenrotation und Extension unterstützen können. Und durch ihren lateralen Zug am Oberschenkel stellen die beiden Gesäßmuskeln die wichtigsten Abduktoren des Hüftgelenks dar.

Wohingegen die hinteren Anteile der kleinen Gesäßmuskeln also auch die Außenrotation unterstützen können, sind die wichtigsten Muskeln hierfür der obturatorius internus, obturatorius externus, gemellus superior, gemellus inferior, quadratus femoris und der piriformis, welche als Außenrotatoren zusammengefasst werden können. Die Außenrotatoren sind mehrere kleine Muskeln, die bis auf den Piriformis am Sitz- oder Schambein entspringen und hin zum Oberschenkelkopf verlaufen. Zusammen drehen sie den Oberschenkel nach außen. Auch der Gluteus maximus unterstützt die Außenrotation.

Adduktoren

Abduktoren und Adduktoren sind Muskeln, welche abspreizen oder aber anziehen, also im Falle des Hüftgelenkes den Oberschenkel in der Frontalebene von der Körpermitte abduzieren (abspreizen) oder zur Mitte adduzieren (anziehen). Die wichtigsten Abduktoren, nämlich der Gluteus medius und minimus wurden ja bereits angesprochen. Die Adduktoren des Hüftgelenks sind Teil der inneren Hüftmuskulatur und erstrecken sich vom unteren Beckenknochen zum Femur und zur Knieregion. Sie verlaufen also auf der Innenseite der Oberschenkel, zwischen der Flexorgruppe und der Extensorgruppe der Oberschenkelmuskulatur.

Die Adduktoren bestehend aus einer ganzen Reihe von Muskeln. Dazu zählen der Adductor longus, Adductor brevis, Adductor magnus, Pectineus und der Gracilis. Sie verlaufen alle entweder vom Sitz- oder aber Schambein hin zum Oberschenkelknochen (oder im Falle des Gracilis auch zum Unterschenkel). Aber auch andere Muskeln wie der Quadratus femoris, oder die kaudalen Anteile des Gluetus maximus unterstützen die Adduktion.

Die Hauptfunktion der Adduktoren ist, dem Namen entsprechend, die Adduktion des Oberschenkels im Hüftgelenk. Je nach Lage des einzelnen Muskels können die Adduktoren aber auch an Flexion und Extension bzw. Außenrotation und Innenrotation im Hüftgelenk beteiligt sein. Dementsprechend gilt zum Beispiel der Adductor magnus, welcher im Verhältnis weiter dorsal (hinten) am Sitzbein entspringt, auch als Hüftstrecker und ein Muskel wie der Adduktor longus, der am Schambein entspringt, kann die Hüft-Flexion unterstützen. Der Gracilis bewegt als einziger zweigelenkiger Adduktor auch das Kniegelenk, wo er eine Flexion und Innenrotation bewirkt.

Gluteus maximus

Der „musculs glutaeus maximus“ ist der große Gesäßmuskel und bildet die oberste Schicht der dorsalen Gesäßmuskulatur, das heißt, er verdeckt nicht nur den Großteil seiner kleineren Namensvetter, Gluteus medius/minumus, sondern auch die ganze Gruppe der Außenrotatoren und prägt damit das Oberflächenrelief der Gesäßregion am stärksten.

Der Gluteus maximus ist ein sehr breit gefächerter Muskel, was auch für seinen Ursprung gilt. Er entspringt vom Darmbeinkamm, der Rückfläche von Kreuz- und Steißbein, dem Ligamentum sacrotuberale (ein flaches Band am hinteren Teil des Beckens, zwischen dem Kreuzbein und dem Sitzbein) und der Fascia thoracolumbalis (eine große Faszienplatte, welche die Muskelgruppe der Rückenstrecker überdeckt und als Ursprung vieler Muskeln, wie dem Gluteus, aber auch z.B. dem Latissimus dient). Die Muskelfasern laufen zu einer gemeinsamen, kräftigen Ansatzsehne zusammen. Die kaudalen (unteren, Richtung Füße gelegenen) Fasern setzen am hinteren Femur an, die kranialen (oberen, Richtung Kopf gelegenen) Fasern dagegen verlaufen in ein kräftiges Sehnenband an der Außenseite des Oberschenkels (tractus iliotibialis).

Die Bewegungsauswirkungen des Gluteus maximus auf den Oberschenkel im Hüftgelenk sind vielfältig und je nach Muskelportion unterschiedlich. Zum einen ist der Glutaeus maximus der stärkste Extensor (Strecker) und Außenrotator des Hüftgelenkes. So sorgt der Glutaeus auch dafür, dass man überhaupt erst aufrecht stehen kann und nicht nach vorne einklappt. Durch seine große Fläche unterstützen zudem seine kranialen (oberen) Fasern die Abduktion und seine kaudalen (weiter unten gelegenen) Fasern die Adduktion, weil sie oberhalb bzw. unterhalb der Abduktions-/Adduktionsachse verlaufen.

Hüftbeuger

Der umgangssprachlich als „Hüftbeuger“ bezeichnete Muskel ist der sogenannte „Lenden-Darmbeinmuskel“. Ganz seinem Alias entsprechend ist dieser Muskel hauptsächlich für die Hüftbeugung, also Flexion im Hüftgelenk verantwortlich. Dabei kann man den Muskel in zwei kleinere Muskeln unterteilen, den Psoas major und den Iliacus. Der psoas major entspringt vom zwölften Brustwirbelkörper, den ersten vier Lendenwirbelkörpern sowie von den Querfortsätzen des ersten bis fünften Lendenwirbels. Der Iliacus entspringt hingegen an der Innenseite der Darmbeinschaufel. Beide verlaufen an der Innenseite des Hüftgelenkes, vereinen sich zu einem Muskel, den Iliopsoas und setzen kurz unterhalb des Schenkelhalses an.

Der illiopsoas ist der stärkste Hüftbeuger und damit maßgeblich bei Laufbewegungen, bzw. bei allen Bewegungen beteiligt, bei denen der Oberschenkel nach vorne angehoben wird. In Rückenlage unterstützt er im Umkehrschluss das Aufrichten des Körpers. Damit ist er ein Gegenspieler des Glutaeus Maximus.

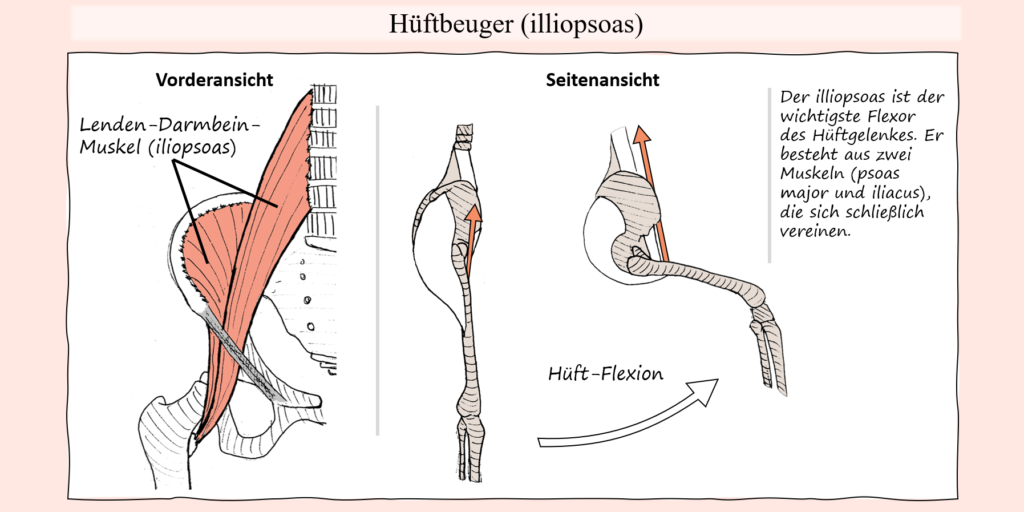
Bewegung	Ziel	Bewegungs-richtung (Zugrichtung)	Agonist	Ursprung	Ansatz
gluteale Muskeln
Stabilisiert das Becken, dass dieses beim Gehen oder Einbeinstand nicht abkippt	Oberschenkel	Abduktion	Gluteus medius	glutealen Seite der Darmbeinschaufel	großer Rollhügel
Stabilisiert das Becken, dass dieses beim Gehen oder Einbeinstand nicht abkippt	Oberschenkel	Abduktion	Gluteus minumus	glutealen Seite der Darmbeinschaufel	großer Rollhügel
beugt den Ellbogen und richtet die Hand neutral aus	Oberschenkel	Flexion; Außenrotation; Adduktion; Abduktion	Gluteus maximus	Darmbeinschaufel, Rückfläche von Kreuz- und Steißbein, Ligamentum sacrotuberale Fascia thoracolumbalis	Hinterseite des Oberschenkelknochen-Schafts (Tuberositas glutealis) und Sehnenband an der Außenseite des Oberschenkels (Tractus iliotibialis)
Illiopsoas Muskeln
Hebt das Bein nach vorne an, richtet den zurückgeneigten Oberkörper auf	Oberschenkel	Flexion	illiacus	Innenseite der Darmbeinschaufel	Kleiner Rollhügel unterhalb des Schenkelhalses
Hebt das Bein nach vorne an, richtet den zurückgeneigten Oberkörper auf	Oberschenkel	Flexion	Psoas major	12. Brust und 1.-4. Lendenwirbel, Querfortsätze der Lendenwirbel	Kleiner Rollhügel unterhalb des Schenkelhalses
Außenrotatoren
Drehen das Bein nach außen, helfen beim Abspreizen und unterstützen Hüftbeugung/ Streckung	Oberschenkel	Außenrotation, Abduktion	Piriformis, Gemellus superior, Obturatorius externus, Gemellus inferior, Quadratus femoris)	Hüftbein, Schambein, Sitzbein	Rückseite des großen Rollhügels
Adduktoren
Ziehen die Beine an den Körper und unterstützen Beugung / Streckung der Hüfte	Oberschenkel (Gracilis auch Unterschenkel)	Adduktion, Flexion, Extension	Adductor magnus, Adductor longus, Adductor brevis, Pectineus, (Gracilis)	Schambein; Sitzbein	Flächenförmig an der Rückseite des Oberschenkels

Oberschenkelmuskeln, die Femur, Schienbein und Wadenbein bewegen

Die Oberschenkelmuskeln, welche den Ober- und Unterschenkel bewegen, können anatomisch grob in posterior und anterior unterteilt werden, also Muskeln, welche sich auf der Oberschenkelvorderseite oder Rückseite befinden.

Die Muskeln des vorderen Oberschenkelkompartiments beugen den Oberschenkel und strecken das Bein. Dieses Fach enthält die Gruppe des Quadrizeps femoris, die eigentlich aus vier Muskeln besteht, die das Knie strecken und stabilisieren.

Das hintere Kompartiment des Oberschenkels umfasst Muskeln, die das Bein beugen und den Oberschenkel strecken. Die drei langen Muskeln auf der Rückseite des Knies bilden die hintere Beinbeuger-Gruppe, die das Knie beugt.

Oberschenkelvorderseite; Quadrizeps femoris

Der Quadrizeps, oder „musculus quadriceps femoris“, ist eine Muskelgruppe, welche sich aus vier Muskeln zusammensetzt und den Großteil des Oberschenkelknochens abdeckt.

Dabei unterscheidet man den „rectus femoris“ (geraden Schenkelmuskel), den „vastus intermedius“ (mittleren Schenkelmuskel), den „vastus lateralis“ (äußeren Schenkelmuskel) und den „vastus medialis“ (inneren Schenkelmuskel).

Der rector femoris ist der einzige zweigelenkige Muskel der Quadrizeps-Gruppe und entspringt zweigeteilt am Darmbeinstachel und am Oberrand der Hüftgelenksspfanne. Er zieht sowohl über das Kniegelenk als auch das Hüftgelenk.

Der vastus intermedius wird vollständig vom rectus femoris verdeckt. Er entspringt an den frontalen und lateralen Flächen der oberen zwei Drittel des Oberschenkelknochens und verläuft direkt am Knochen entlang Richtung Knie.

Der vastus lateralis ist in der Regel der größte und stärkste Muskel des Quadrizeps. Er entspringt lateral am proximalen Oberschenkelknochen und verlauft auch Richtung Knie.

Der vastus medialis, also der innere Schenkelmuskel entspringt an der Medialseite des Oberschenkelknochens und verläuft dann auch an der Innenseite Richtung Knie.

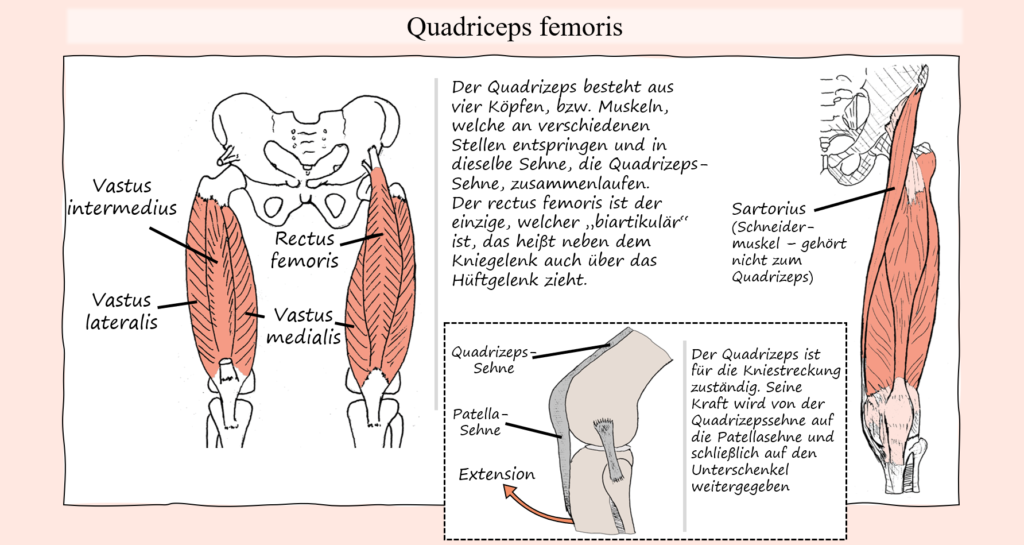
Einheitlich laufen alle Muskeln des Quadrizeps oberhalb der Patella in die Quadrizepssehne zusammen. Einige Fasern ziehen über die Kniescheibe hinweg und schließen die Patella so als Sesambein ein. Der funktionelle Nutzen der Patella wurde bereits erwähnt. Die Patella-Sehne setzt dann wiederum unterhalb des Kniegelenkes am Schienbein an und überträgt die Kraft des Quadrizeps auf den Unterschenkel.

Der Quadrizeps ist der einzige Streckmuskel des Kniegelenks und spielt deshalb eine entscheidende Rolle bei allen Bewegungen, in denen eine Extension des Knies notwendig ist (z.B. Gehen oder aus sitzender Position aufstehen). Im Stand verhindert er ebenso das Einknicken des Kniegelenks. Der rectus femoris kann zusätzlich auch das Hüftgelenk beugen, jedoch ist seine Wirkung relativ schwach.

Ein weiterer Muskel der Oberschenkelvorderseite, welcher aber nicht zum Quadrizeps zählt, ist der musculus sartorius, oder auch „Schneidermuskel“ genannt. Der Sartorius ist ein schmaler, schlangenförmiger Muskel, der sich um den ganzen Oberschenkel legt. Er entspringt an der Vorderseite des Darmbeins und verläuft spiralförmig über den Oberschenkel, wo er dann auf der Beininnenseite, unterhalb des Kniegelenkes am Schienbein ansetzt. Damit ist er ein zweigelenkiger Muskel und bewirkt sowohl im Hüft- als auch im Kniegelenk eine Flexion. Die Knieflexion kommt deswegen zustande, weil er hinter der Beuge-Streck-Achse ansetzt. Zur Flexion hinzukommt eine leichte Abduktion und Außenrotation des Oberschenkels und, bei gebeugtem Knie, eine leichte Innenrotation des Unterschenkels. In Summe ist dies auch der Grund für seinen deutschen Namen „Schneidermuskel“, weil die Kombination aus Hüftflexion, Knieflexion, Abduktion und Außenrotation der Hüfte, sowie Innenrotation im Knie der Schneidersitz-Position entspricht.

Oberschenkelrückseite; Knieflexoren (Beinbeuger-Gruppe)

Die Knieflexoren, oder auch „ischiocrurale Muskulatur“ genannt befindet sich auf der dorsalen Seite des Oberschenkels und ist der Antagonist des Quadrizeps. Im Gegensatz zum Quadrizeps, der hauptsächlich für die Kniestreckung verantwortlich ist und lediglich der M. rectus femoris über Knie und Hüfte zieht, ist die ischiocrurale Muskulatur zweigelenkig und zieht nicht nur über das Knie, sondernauch über das Hüftgelenk. Die Bezeichnung „ischiocrural“ folgt von ihrem Ursprung am Sitzbein („Os ischii“). Die Muskelgruppe umfasst drei einzelne Muskeln, den „musculus biceps femoris“ (Beinbizeps), den „musculus semitendinosus“ (Halbsehnenmuskel) und den „musculus semimembranosus“ (Plattsehnenmuskel).

Der biceps femoris, auch zweiköpfiger Schenkelmuskel genannt, nimmt den größten Teil der ischiocrurale Muskulatur ein und besitzt zwei Köpfe. Der lange Kopf entspringt am Sitzbein. Der kurze Kopf entspringt entlang der Rückseite des Oberschenkelknochens. Beide Köpfe setzen dann mit derselben Sehne am Wadenbeinköpfchen, also am lateralen Unterschenkel an.

Der semitendinosus, oder Halbsehnenmuskel, hat seinen Namen dadurch, weil die Ansatzsehne im Verhältnis zur Gesamtlänge des Muskels sehr lang ist. Er entspringt an derselben Ursprungssehne wie der biceps femoris und setzt an der medialen Seite des proximalen Unterschenkels (Innenseite) am Schienbein durch eben erwähnte Sehne an. In der Skizze in Abbildung 15 ist der Halbsehnenmuskel schwarz dargestellt, um den teilweise darunterliegenden Plattsehnenmuskel erkennbar zu machen.

Der semimembranosus, oder Plattsehnenmuskel entspringt am Sitzbein,
medial, der Ursprungsstelle des langen Bizepskopfes. Er verläuft erst als breite Sehnenplatte dorso-lateral am Oberschenkel entlang, bis er in der unteren Hälfte einen Muskelbauch ausbildet und medial am Unterschenkel, bzw. der Gelenkkapsel ansetzt.

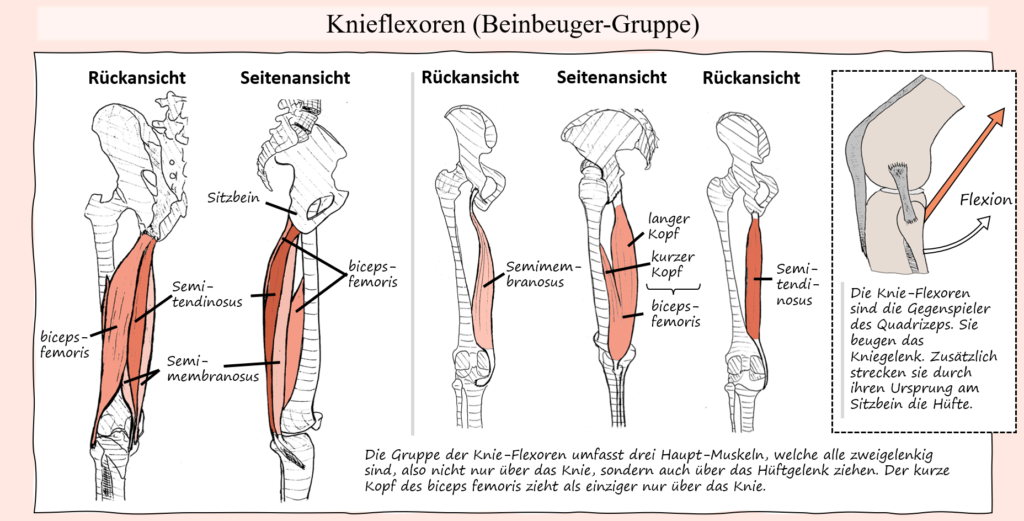
Als zweigelenkige Muskelgruppe zieht die ischiocrurale Muskulatur sowohl über Hüfte als auch Knie. Durch ihren Verlauf auf der Oberschenkelrückseite vom Sitzbein hin zum Unterschenkel bewirken sie eine Flexion im Kniegelenk und eine Extension, also Streckung (Aufrichtung) im Hüftgelenk, wobei sie etwas mehr im Bereich des Kniegelenks wirkt.

Diese zwei großen Bewegungsfunktionen erfüllen alle drei Muskeln, da sie allesamt am Sitzbein entspringen und am Unterschenkel ansetzen. Je nach Ansatz auf medialer oder lateraler Seite tragen sie aber auch zur Außen- bzw. Innenrotation bei. Durch ihren medialen Ansatz rotieren der semitendinosus sowie semimembranosus den Unterschenkel demnach leicht nach innen. Dabei ist die Innenrotation des Knies im Vergleich zur Außenrotation geringer, weil sich die Kreuzbänder „ineinander- drehen“. Der biceps femoris hingegen setzt lateral am Unterschenkel an und sorgt somit für eine Außenrotation. Dabei ist er der einzige Muskel, der das Kniegelenk in gebeugter Position nach außen rotieren kann. Des Weiteren ist der kurze Kopf des biceps femoris der einzige, welcher nicht zweigelenkig ist und nur über das Kniegelenk zieht (er hat also keine direkte Auswirkung auf das Hüftgelenk).

Bewegung	Ziel	Bewegungs-richtung (Zugrichtung)	Agonist	Ursprung	Ansatz
mediale Oberschenkelmuskeln, die den Unterschenkel bewegen
beugt das Knie, zählt zu den Adduktoren	Oberschenkel; Unterschenkel	Unterschenkel: Flexion; Oberschenkel: Adduktion	Gracilis	Schambein und Beckensymphyse	Mediale Oberfläche des Schienbeins
Anteriorer Oberschenkelmuskeln, die den Unterschenkel bewegen
Kniestreckung; unterstützt Anheben des Beines nach vorne	Oberschenkel; Unterschenkel	Unterschenkel: Extension; Oberschenkel: Flexion	Rectur femoris	Darmbeinstachel Und Oberrand der Hüftgelenksspfanne	Patella; proximales vorderes Schienbein
Kniestreckung	Unterschenkel	Extension	Vastus lateralis	Proximaler, lateraler Oberschenkelknochen	Patella; proximales vorderes Schienbein
Kniestreckung	Unterschenkel	Extension	Vastus medialis	Medialseite des Oberschenkelknochens	Patella; proximales vorderes Schienbein
Kniestreckung	Unterschenkel	Extension	Vastus intermedius	vorderen proximalen Flächen des Oberschenkelknochens	Patella; proximales vorderes Schienbein
Scheineidersitz-position	Oberschenkel; Unterschenkel	Unterschenkel: Flexion; Oberschenkel: Flexion, Adbuktion, Außenrotation	Sartorius	Vorderseite des Darmbeins	Proximales, mediales Schienbein
posteriore Oberschenkelmuskeln, die den Unterschenkel bewegen
Beugt das Knie und streckt die Hüfte	Oberschenkel; Unterschenkel	Unterschenkel: Flexion; Oberschenkel: Extension, Außenrotation	Biceps femoris	Sitzbein; distaler Femur	Wadenbeinkopf; proximales, laterales Schienbein
Beugt das Knie und streckt die Hüfte	Oberschenkel; Unterschenkel	Unterschenkel: Flexion; Oberschenkel: Extension, Innenrotation	Semitendinosus	Sitzbein	proximales, mediales Schienbein
Beugt das Knie und streckt die Hüfte	Oberschenkel; Unterschenkel	Unterschenkel: Flexion; Oberschenkel: Extension, Innenrotation	Semimembranosus	Sitzbein	proximales, mediales Schienbein

Muskeln, die die Füße bewegen

Ähnlich wie auch der Oberschenkel kann auch die Muskulatur des Unterschenkels in Regionen eingeteilt werden, in diesem Fall posterior, anterior und lateral. Die Muskeln, die hier zu finden sind, sind vorwiegend zuständig für die Fußgelenke und Zehen, ebenso wie die intrinsischen Muskeln des Fußes. Wie auch schon im Falle der Hand verzichten wir in diesem Kontext aber auf eine detaillierte Betrachtung dieser vielen einzelnen Muskeln. Ein, oder vielmehr zwei Muskeln sind aber auch hier hilfreich zu erwähnen. Und zwar die oberflächlichen Flexoren des Fußgelenkes, welchen beim Gehen und sämtlichen Laufbewegungen eine wichtige Rolle zukommt.

Oberflächliche Flexoren; Wadenmuskulatur

Die oberflächlichen Flexoren des Unterschenkels werden oftmals schlicht als „Wadenmuskulatur“ bezeichnet und umfassen drei Muskeln, den gastrocnemius, den soleus und den plantaris. Vor allem erstere beide nehmen den Großteil des posterioren Unterschenkels ein und dadurch, dass beide Muskeln die Achillessehne als Ansatz haben und funktionell sehr eng zusammenarbeiten, werden sie auch oftmals als ein dreiköpfiger Muskel (triceps surae) zusammengefasst.

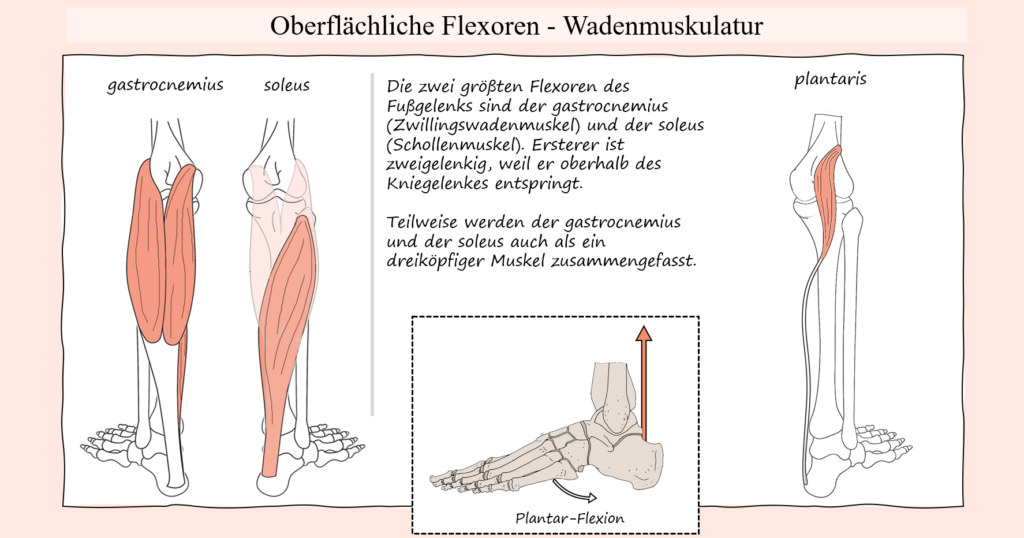
Der „musculus gastrocnemius“, oder „Zwillingswadenmuskel“, ist ein zweiköpfiger Muskel und gibt der Wade ihre typische Form. Seine beiden Köpfe, caput mediale und caput laterale, entspringen an einem medialen bzw. lateralen Knochenvorsprung des Oberschenkelknochens oberhalb des Knies. Die beiden Köpfe treffen sich bereits sehr früh und verschmelzen zu einem dicken Muskelbauch, dessen Endsehne mit der des soleus verschmilzt und die Achillessehne bildet. Diese wiederum setzt am Fersenbein an.

Der „musculus soleus“ entspringt am Kopf und dem oberen Drittel der Dorsalflächen von Wadenbein und Schienbein. Er wird fast vollständig vom gastrocnemius verdeckt, lediglich an den Seitenrändern des gastrocnemius ist der Muskelbauch sichtbar.

Der „musculus plantaris“ ist im Vergleich zum gastrocnemius und soleus recht klein und besitzt nur einen kleinen Muskelbauch. der in eine lange dünne Sehne (30-40 cm) ausstrahlt. Sein Ursprung liegt oberhalb der lateralen Kondyle des Oberschenkelknochens, oberhalb vom Ursprung des Caput laterale des gastrocnemius. Auch dieFasern der langen Sehne des plantaris strahlen in die Faszie des soleus und die Achillessehne ein.

Die wesentliche Aufgabe der Flexoren des Unterschenkels, vor allem des triceps surae, ist die Plantarflexion im oberen Sprungelenk sowie eine gewisse Inversion im unteren Sprunggelenk. Aufgrund des kleinen Muskelbauches (und folglich wenig Kraft) des plantaris kann seine Bewegungsfunktion im Vergleich vernachlässigt werden. Im Gegensatz zum soleus zieht der gastrocnemius auch über das Kniegelenk, was dazu führt, dass er auch die Knie-Flexion unterstützt.

Zu den „oberflächlichen Flexoren“ hinzukommen tiefer liegende Flexoren, welche aber Grund-, Mittel-und Endgelenke der Zehen kontrollieren, aber auch zur Plantarflexion beitragen. Ebenso wie natürlich Muskeln auf anteriorer und lateraler Seite, welche hingegen die Eversion, Dorsalflexion und das Anheben der Zehen ermöglichen.

Axiale Muskeln der Bauchdecke, des Thorax, Nacken und Rückens

Den Körper auf zwei Beinen zu balancieren und aufrecht zu gehen ist eine komplexe Aufgabe, welche die Zusammenarbeit einer Vielzahl von Muskeln bedarf. Die Muskeln der Wirbelsäule, des Brustkorbs und der Bauchdecke strecken, beugen und stabilisieren verschiedene Teile des Körperrumpfs. Die Tiefenmuskulatur der Körpermitte hilft dabei, die Körperhaltung aufrechtzuerhalten und andere Funktionen auszuführen. Die wesentlichen Muskeln, die für die Kontrolle des Schulter- und Beckengürtels als auch der Extremitäten zuständig sind, wurden in den obigen Abschnitten bereits erwähnt. Im Folgenden sehen wir uns noch zwei zentrale Muskelgruppen an, welche zum einen die Wirbelsäule und zum anderen die Bauchwand stabilisieren bzw. kontrollieren und damit zentrale Schlüsselrollen für das Zusammenspiel des Körpers als funktionelle Einheit ergeben.

Wirbelsäule

Die Wirbelsäule ist ein zentrales Bindungsglied unseres Bewegungsapparates. Sie dient nicht nur als Verbindung des Achsenskeletts mit den Extremitäten, sondern auf ihr lastet darüber hinaus auch der Brustkorb sowie der Kopf und die oberen Extremitäten. Durch das sogenannte Wirbelloch in den einzelnen Wirbeln entsteht der Wirbelkanal, indem das Rückenmark verläuft. Hier laufen Nerven, welche unseren ganzen Körper vernetzen.

Die Wirbelsäule selbst ist aufgebaut aus 24 bzw. 33/34 Wirbeln. Dabei unterscheiden wir zwischen 7 Halswirbeln, 12 Brustwirbeln und 5 Lendenwirbeln. Entsprechend unterscheidet man so auch zwischen Lendenwirbelsäule, Brustwirbelsäule und Halswirbelsäule. Hinzukommen weitere 5 (verschmolzene) Wirbel, die das Kreuzbein sowie weitere 3-5 verknöcherte Wirbel, die das Steißbein bilden.

Die Wirbelsäule bildet die knöcherne Mitte des Körpers, sie ist das Grundelement des Achsenskeletts, an ihr ist der Brustkorb, der Beckengürtel und zahlreiche Muskeln verbunden, sie schützt das Rückenmark im Wirbelkanal, Lasten, die auf dem Oberkörper liegen, werden

über die Wirbelsäule auf das Becken und die untere Extremität übergeben, durch ihre S-Form federt sie Bewegungen ab, kann sehr hohen Belastungen standhalten, ermöglicht aber trotzdem viel Beweglichkeit im Rumpf.

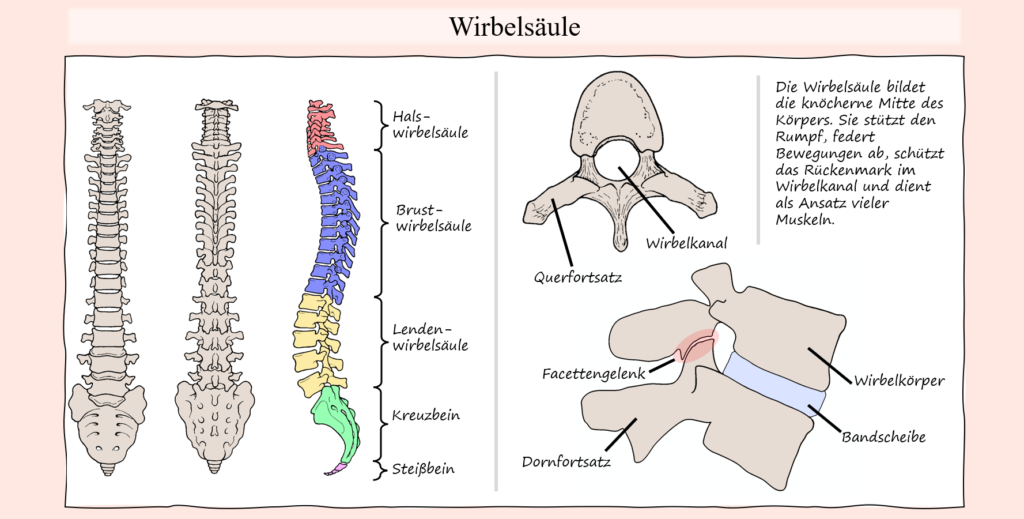
Optisch kennzeichnet sich die Wirbelsäule durch ihre charakteristische doppelte S-Form und ihrem Aufbau aus den vielen einzelnen Wirbelkörpern, die mittels Bandscheiben und Facettengelenken miteinander verbunden sind. Dieser Aufbau ermöglicht es Lasten besser abzufangen, sehr hohen Belastungen standzuhalten, aber gleichzeitig beweglich zu bleiben.

Die Wirbel selbst haben einen grundlegend gleichen Aufbau, auch wenn sich das Aussehen von Hals-, Brust-, und Lendenwirbel unterscheidet. Sie besitzen einen Wirbelkörper, einen Wirbelbogen, einen Dornfortsatz, zwei Querfortsätzen sowie Gelenkfortsätzen. Dabei bildet der untere Gelenkfortsatz des einen mit dem oberen Gelenkfortsatz des benachbarten Wirbels ein planes Gelenk („Zwischenwirbelgelenk“ oder „Facettengelenk“).

Die Stellung der Gelenkflächen variiert in den verschiedenen Abschnitten der Wirbelsäule, genauer gesagt sind die Gelenkflächen je nach Wirbelsäulenabschnitt, in unterschiedlichem Ausmaß gegen die Horizontale (und Vertikale) geneigt und damit auf bestimmte Bewegungsrichtungen sowie ein bestimmtes Bewegungsausmaß spezialisiert:

Bei der Halswirbelsäule stehen die Gelenkflächen benachbarter Wirbel eher in der Transversalebene, die Gelenkfortsätze weisen nach dorsal und etwas nach kranial. Dies ermöglicht eine ausgeprägte Rotationsbewegung, aber auch Lateralflexion und Ventralflexion/Dorsalextensionder der Halswirbelsäule. Die Halswirbelsäule ist damit der beweglichste Wirbelsäulenabschnitt.

Bei der Brustwirbelsäule schauen die Gelenkflächen ebenfalls nach dorsal und kranial, sind aber bereits zusätzlich nach lateral geneigt. Außerdem werden die Bewegungsmöglichkeiten der Brustwirbelsäule durch die Verbindung zu Rippen/Thorax erheblich verringert.

Die Lendenwirbelsäule weist Gelenkflächen auf, die fast in der Sagittalebene stehen, weswegen die Rotationsmöglichkeiten hier stark eingeschränkt sind. Die bevorzugte Bewegung der Lendenwirbelsäule ist die Ventralflexion und die Dorsalextension (nach vorne beugen und aufrichten).

Auf der Vorder- und Rückseite sind die Wirbelkörper mit Bändern verbunden und gewinnen so an Halt. Zwischen den Wirbelkörpern benachbarter Wirbel befinden sich die Bandscheiben, welche mit den Deckflächen der Wirbelkörper fest verwachsen sind. Die Bandscheiben fungieren als elastisches Druckpolster, die zum einen die Belastung der Wirbelsäule abfangen und gleichmäßig auf die gesamte Oberfläche der angrenzenden Deckplatten aufteilen, aber auch zur Beweglichkeit beitragen.

Die Position der Wirbelkörper wird von der ihr aufliegenden (autochthonen) Rückenmuskulatur, kontrolliert. Sie erstreckt sich auf beiden Seiten entlang der Wirbelsäule vom Becken über den Brustkorb bis hin zum Kopf und wird wegen ihrer Funktion als Aufrichter und Stabilisator der Wirbelsäule der Einfachheit halber oft auch als „musculus erector spinae“, oder zu Deutsch „Rückenstrecker“ bezeichnet.

Die Gruppe der erector spinae stellt den größten Teil der Muskelmasse des Rückens dar und ist der primäre Strecker der Wirbelsäule. Es kontrolliert die Beugung, seitliche Beugung und Drehung der Wirbelsäule und hält die Lendenwirbelsäule aufrecht.

autochthone Rücken- und Thoraxmuskulatur

„Autochthon“ beschreibt in der Anatomie „tiefliegende“ Muskulatur, also im Falle des Rückens Muskeln, welche direkt der Wirbelsäule aufliegen und damit unterhalb der großen Muskeln wie dem Latissimus, dem Trapezius und den Rhomboiden, welche weiter oben beschrieben wurden, liegen. Die autochthone Rückenmuskulatur umfasst also die tief liegenden Rückenmuskeln an der Wirbelsäule, die sich vom Becken bis hin zum Kopf erstrecken. Diese Muskelgruppe setzt sich aus sehr vielen einzelnen Muskeln unterschiedlicher Länge zusammen, die sich dann als Ganzes über die gesamte Wirbelsäule erstrecken. Einige Muskeln verlaufen dabei vom Darmbein zu den Rippen, andere erstrecken sich über die gesamte Wirbelsäule und wiederum andere sind sehr kurz und verlaufen nur von Wirbel zu Wirbel.

Die erector spinae-Gruppe kann grob in einen lateralen und einen medialen Trakt, als auch einzelnen Muskelgruppen unterteilt werden. Die jeweiligen Muskeln sind dann nach den Körperbereichen benannt, mit denen sie verbunden sind (also dem Bereich der Wirbelsäule).

Der mediale Trakt erstreckt sich zwischen den Dorn- und Querfortsätzen der Wirbel. Man unterteilt ihn in ein spinales und transversospinales System. Zum spinalen System gehören die muscoli interspinales und der musculus spinalis. Sie verbinden die Dornfortsätze benachbarter Wirbel. (Dazu zählen: Spinalis capitis (Kopfregion), Spinalis cervicis (Halsregion) und Spinalis thoracis (Brustregion) sowie interspinales cervicis (Halsbereich), interspinales thoracis (Brustwirbelsäule), interspinales lumborum (Lendenwirbelsäule). Die transversospinalen Muskeln umfassen die musacoli rotatores breves und longi, den musculus multifidus und musculus semispinalis (Semispinalis capitis, Semispinalis cervicis und Semispinalis thoracis). Sie verlaufen von den Querfortsätzen zu den Dornfortsätzen der Wirbel.

Der laterale Trakt umfasst die splenius-Muskeln, welche an den Dornfortsätzen der oberen Brust- und unteren Halswirbeln entspringen und nach lateral kranial (zum Schädel) ziehen. Sie sind für die Bewegung des Kopfes und der Halswirbelsäule wichtig. Die Iliocostalis-Gruppe und Longissimus-Gruppe beschreiben jeweils drei Muskeln, die sich über verschiedene Bereiche der Wirbelsäule erstrecken. (Iliocostalis cervicis à mit der Halsregion verbunden; Iliocostalis thoracis à mit der Brustregion verbunden; Iliocostalis lumborum à mit der Lendengegend verbunden & Longissimus capitis à mit der Kopfregion verbunden; Longissimus cervicis à mit der Halsregion verbunden; Longissimus thoracis à mit der Brustregion verbunden). Die Musculi intertransversarii, welche auch zum lateralen Trakt zählen, hingegen verbinden die Querfortsätze aneinandergrenzender Wirbel. Auch hier unterschiedet man zwischen Muskeln im Bereich der Hals-, Brust- und Lendenwirbelsäule.

Die autochthone Rückenmuskulatur ist essenziell für die Stabilisierung und Bewegung der Wirbelsäule. Bei beidseitiger Kontraktion kommt es zur Streckung des Körpers (Dorsalextension), bei einseitiger zur Neigung auf entsprechende Seite (Lateralflexion). Die Drehung (Rotation) erfolgt in Zusammenarbeit mit den schrägen Bauchmuskeln.

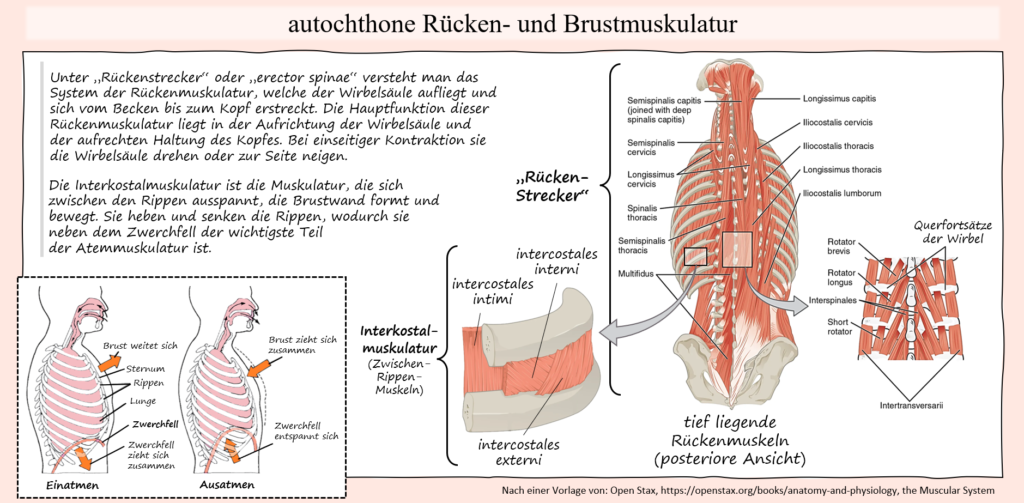
Das Äquivalent zur autochthonen Rückenmuskulatur im Falle des Brustkorbes, beschreibt die tiefliegende Muskulatur, die sich zwischen den Rippen ausspannen und als Interkostalmuskulatur bezeichnet wird. Dazu zählen die „musculi intercostales externi“, „musculi intercostales interni“ und „musculi intercostales intimi“, welche ihrer Benennung entsprechend drei Schichten ergeben. Funktionell gesehen zählt die Interkostalmuskulatur zu den Atemmuskeln, sie hebt und senkt die Rippen und bewirkt so eine Inspiration und Exspiration. Zusammen mit dem Zwerchfell sind sie die wichtigsten Atemmuskeln.

Das Zwerchfell ist der zentrale Atemmuskel, der den Bauchraum nach kranial hin zur Brusthöhle verschließt. Es entspringt an den unteren Rippen, der Lendenwirbel sowie am Brustbein und ragt als eine gewölbte Muskelscheibe in den Brustkorb hinein. Kontrahiert das Zwerchfell, wird diese Wölbung flacher, wodurch der Brustraum vergrößert und Luft eingesogen wird. Eine Kontraktion des Zwerchfells führt zu einer Vergrößerung des Thoraxraumes und einer Formveränderung des Abdominalraumes. Dadurch wiederum wird das Lungenvolumen vergrößert, und der entstehende Unterdruck führt zur Einatmung. Des Weiteren dient die Zwerchfellkontraktion der Bauchpresse (durch das Einatmen und Kontraktion des Zwerchfelles, bei gleichzeitiger Kontraktion der Bauchwand wird der intraabdominale Druck erhöht), beispielsweise beim Geburtsvorgang, der Defäkation (Stuhlgang) oder auch körperlicher Belastung.

Muskulatur der Bauchwand

Als Bauchmuskulatur gilt die in der Bauchwand und Bauchregion lokalisierte Muskulatur. Die Bauchwand umgibt, als flexible Hülle, die Bauchhöhle und verbindet den Beckenring mit dem Brustkorb. Begrenzt wird die Bauchwand superior (oben) vom Sternum und den Sippenbogen auf beiden Seiten, dorsal (hinten) grenzt sie an die Wirbelsäule und inferior (unten) an die Beckenknochen. Als Ganzes kann sie in einen ventralen (vorderen), lateralen (seitlichen) und dorsalen (hinteren) Bereich unterteilt werden und das Gleiche gilt für die Muskulatur, wo man die anterolaterale Bauchmuskulatur und die posteriore Bauchwandmuskulatur unterscheidet.

Es gibt vier Bauchmuskelpaare, die den anterioren und lateralen Bauchbereich bedecken und sich an der vorderen Mittellinie treffen. Diese Muskeln der anterolateralen Bauchwand können in vier Gruppen eingeteilt werden:

die äußeren schrägen Bauchmuskeln (obliquus externus abdominis)
die inneren schrägen Bauchmuskeln (obliquus internus abdominis)
den Transversus abdominis
den vorderen geraden Bauchmuskeln (rectus abdominis)

Der obliquus externus abdominis, der der Oberfläche am nächsten liegt, erstreckt sich nach unten und medial. Nahezu senkrecht dazu verläuft der intermediäre obliquus internus abdominis, der sich nach oben und nach medial erstreckt. Der tiefliegende Muskel Transversus abdominis, ist hingegen quer um den Bauch herum angeordnet, ähnlich wie ein Gürtel, der die Bauchwand umschließt. Diese Anordnung von drei „Muskelbändern“ in unterschiedlicher Ausrichtung ermöglicht verschiedene Bewegungen und Rotationen des Rumpfes. Die drei Muskelschichten tragen auch dazu bei, die inneren Bauchorgane in einem Bereich zu schützen, in dem es keine Knochen gibt. Die Aponeurosen der drei seitlichen Bauchmuskeln bilden die Rektusscheide (Aponeurosen sind flächige Strukturen aus Bindegewebe, die als sehniger Ansatz eines oder mehrerer Muskeln dienen). Diese rektusscheide umschließt den rectus abdominis (die vorderen, geraden Bauchmuskeln), der sich vom Schambeinkamm und der Symphyse über die Länge des Körperrumpfs bis zum Sternum erstreckt. Dadurch, dass der rectus abdominis durch Querbänder aus Kollagenfasern segmentiert wird, bilden sich einzelne Muskelbäuche, die zum allseitsbekannten „Sixpack“ führen (wobei nicht jeder Mensch die gleiche Segmentierung aufweist).

Die posteriore Bauchwand wird von den Lendenwirbeln, Teilen der Darmbeine, der Hüftknochen, dem psoas major und dem iliacus, welche aber vereinzelt nicht zur Bauchmuskulatur gezählt werden, sowie dem musculus quadratus lumborum gebildet. Dieser Teil des Rumpfes spielt eine Schlüsselrolle bei der Stabilisierung des restlichen Körpers und der Aufrechterhaltung der Körperhaltung.

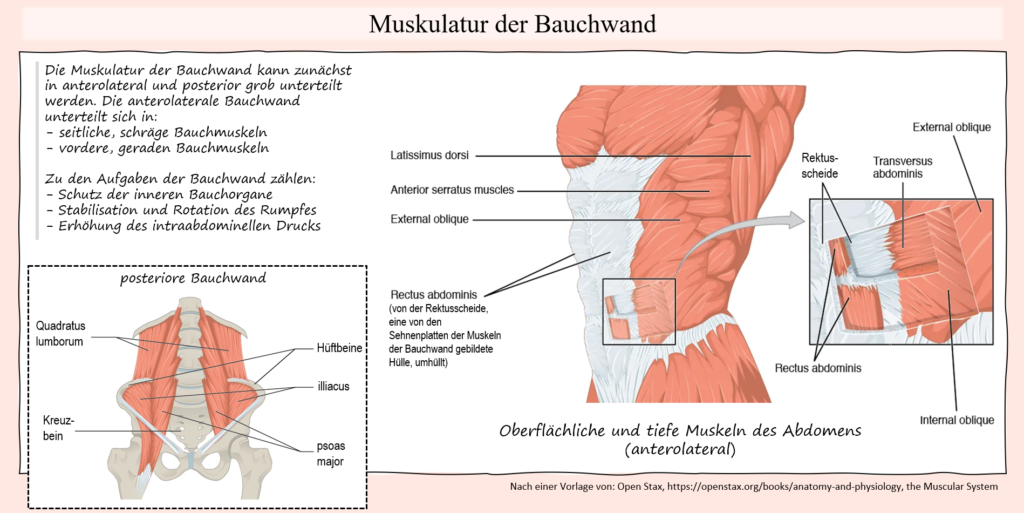
Funktionelle Anatomie im Trainingskontext

Die Anatomie ist die beschreibende Lehre vom Aufbau bzw. der Gestalt des menschlichen Körpers und seiner Gewebe, als auch deren Entwicklung. Die „funktionelle Anatomie“ hingegen ist eine Methodik der Anatomie, welche sich nach dem Motto „form follows function“ mit der Verbindung des Aufbaus einer anatomischen Struktur mit ihrer jeweiligen Funktion beschäftigt.

In vorherigen Abschnitten wurde bereits das Skelettsystem als auch das umliegende Skelettmuskelsystem beschrieben, wobei der Fokus bereits auf deren funktionellen Rollen lag. Das Mittel hierfür bietet die anatomische Terminologie, welche zu anfangs aufgegriffen wurde und als System für Richtungsangaben und andere anatomischen Beschreibungen dient. Die anatomische Normalposition diente hierbei nicht nur als Referenz, auf welche die anatomische Fachsprache verweist, sondern entspricht dementsprechend auch der gängigen Position, von der aus, allgemeine anatomische Beschreibungen gemacht werden. So sind z.B. in Lehrbüchern die in grafischen Darstellungen aufgezeigten menschlichen Körper, anhand derer bestimmte Strukturen gezeigt werden, natürlich sehr oft in der Normalposition abgebildet. In aller Regel bringt dies nämlich Vorteile mit sich, weil die Terminologie, welche genutzt wird, um die Darstellung zu beschreiben, nun mal auf der Normalposition basiert und sich dadurch die Beschreibung mit dem Beschreibenden deckt. Würde eine dargestellte Person z.B. die Arme ausgestreckt über dem Kopf halten, so würde sich anatomisch gesehen der Ellbogen immer noch superior der Hand befinden, auch wenn die Hand in dieser Position weiter oben als der Ellbogen ist. Durch eine Darstellung in der Normalposition können demnach Missverständnisse möglichst verhindert werden. Wenn es aber um Funktionen, gerade der Skelettmuskulatur geht, dann geht es darum zu verstehen, welche funktionelle Rolle jeweilige Muskeln innerhalb des gesamten Bewegungsrahmens erfüllen. Das wiederum bedeutet, es geht zwangsweise um Betrachtungen, die über die Normalposition hinausgehen. Das ist deswegen wichtig, weil die Bewegungsfunktion, welche ein Muskel erfüllt, mitunter von der jeweiligen Körper- bzw. Gelenkposition abhängt. Wenn also ein Muskel zur Adduktion des Armes beiträgt, dann macht er dies, weil die Zugrichtung, welche er bei gegebener Körperposition auf den Knochen ausübt, eine Adduktion zur Folge hat. Das wiederum bedeutet aber nicht gleich, dass dieser Muskel unabhängig von der Gelenkposition auch immer zur Adduktion beiträgt. Glücklicherweise kann man in der Theorie durch Betrachtung des Muskelverlaufes, unabhängig der Position, in welcher sich der Körper gerade befindet, aber schlussfolgern, welche Bewegungsfunktion der Muskel bei beliebigen anderen Positionen erfüllt, dies erfordert aber eine mechanische Betrachtung. Die Biomechanik ist die Lehre vom Menschen in Bewegung und beschreibt im Kontext einwirkender Kräfte und den Eigenschaften des Bewegungsapparates, wie dieser sich bewegt. Streng genommen haben wir genau das bereits gemacht, als wir uns das Skelettmuskelsystem samt den Muskelfunktionen angesehen haben. Beim grundlegenden Gedankengang „wo entspringt ein Muskel, wo setzt er an und was passiert (welche Bewegung wird ausgelöst), wenn dieser Muskel kontrahiert (verkürzt)?“ macht man im Grunde nichts anderes als eine einfache mechanische Analyse, in der man sich schlichtweg vorstellt, welche Bewegung herauskommt, wenn man an dieser einen Stelle am Knochen (Muskelansatzpunkt) in entsprechende Richtung (zum Muskelursprung hin) zieht. Spinnt man das Ganze etwas weiter und bezieht ein, wo sich der Drehpunkt befindet (dazu gleich mehr) und wie der Muskelverlauf in Relation dazu liegt bzw. bei Gelenkbewegungen verändert wird, dann weiß man auch, welche Bewegung bei unterschiedlichsten Gelenkpositionen von einem Muskel erfüllt werden. Oftmals, wie zum Beispiel beim Brachialis ist das Ganze natürlich einfach, weil der Muskel in jeder Position, in die man den Arm bzw. Unterarm bringen kann, was beim Ellbogen wohlgemerkt recht beschränkt ist, zur Ellbogenbeugung führt. Aber es gibt auch andere Beispiele, wo die Bewegungsfunktion eines Muskels in bestimmten Positionen variieren kann. Dazu werden wir uns weiter unten auch einige ausgewählte Beispiele ansehen. Hier ist es dann umso wichtiger, einem Muskel nicht per se gewisse Bewegungsfunktionen zuzuschreiben, sondern eben zu versuchen mechanisch nachzuvollziehen, welche Bewegungsfunktion zutrifft. Nun ist es nicht Sinn und Zweck dieses Abschnittes sich weitreichend mit Biomechanik zu befassen, was vielmehr einen eigenständigen Themenabschnitt bildet, sondern zunächst das funktionelle Verständnis der Skelettmuskulatur auszuweiten. Um das zu erreichen, werden wir, weil Bewegung, einschließlich der Bewegung, welche Muskeln auslösen, mechanischen Gesetzen folgt, etwas vorgreifen und im Folgenden kurz darauf eingehen, wie die Skelettmuskeln den Körper bewegen.

Wenn man an Muskulatur denkt, dann liegt auch der Gedanke an Kraft wahrscheinlich recht nahe. Und tatsächlich, wenn wir Muskulatur erstmal außen vor lassen, stehen Kraft und Bewegung in direkter Verbindung, soll heißen, um Bewegungen auszulösen bzw. eine Bewegungsänderung zu erreichen (egal wovon), muss Kraft mit ins Spiel kommen, denn die Kraft ist der Auslöser eben jener Bewegungsänderung. Wenn man darüber nachdenkt, ist das ziemlich logisch. Steht ein Glas auf einem Tisch, dann wird dieses Glas dort stehen bleiben und sich nicht bewegen, bis irgendwelche Kräfte eine Bewegung verursachen. Ursprung solch einer Kraft kann alles Mögliche sein, eine menschliche Hand, die das Glas anhebt, die Pfote einer Katze, welche das Glas aus irgendeinem Grund unbedingt umwerfen möchte, oder auch ein starker Windstoß, wenn das Küchenfenster offengelassen wurde. Und die Art und Weise, wie die Kraft auf das Glas einwirkt, bestimmt die dadurch ausgelöste Bewegung. Auch das ist einfach zu verstehen. Drückt die Hand seitlich auf der rechten Seite des Glases nach links, dann wird es sich, wenn die Kraft ausreicht, in die Richtung bewegen, in die der Druck der Hand ausgeübt wird, also nach links. Möchte man das Glas hingegen senkrecht nach oben anheben, dann muss Kraft in diese Richtung, also nach oben, ausgeübt werden, sprich die Hand muss das Glas greifen uns nach oben bewegen.

Diese simple Verbindung von Kraft und Bewegung bildet einen Grundbaustein der Mechanik und reicht an diesem Punkt auch bereits vollkommen aus, um etwas genauer darauf einzugehen, wie Skelettmuskulatur nun den Körper bewegt und folglich auf Bewegungsfunktionen beliebiger Muskeln zu schließen.

Damit die Muskeln das Skelett bewegen können, muss also Kraft aufgewendet werden, was zugleich die wesentliche Aufgabe der Skelettmuskulatur ist. Greifen wir also auch hier etwas vor und sehen uns das kurz etwas genauer an. Muskulatur ist eine der vier primären Gewebetypen des menschlichen Körpers und kann weiterhin in drei Unterkategorien unterteilt werden, Skelettmuskulatur, Herzmuskulatur und glatte Muskulatur. Alle drei Typen haben wesentliche Eigenschaften gemeinsam, die sie überhaupt erst zu Muskulatur machen. Der erste und auch wichtigste Punkt ist, dass sie alle dazu in der Lage sind zu kontrahieren, was bedeutet, dass aktiv Kraft erzeugt wird, welche genutzt werden kann, um zum Beispiel eine bestimmte Bewegung auszuführen. Muskulatur ist in unserem Körper also dazu da, um Bewegungen auszuführen und zu kontrollieren. Im Umkehrschluss muss hierzu aber kontrolliert werden, wann die Muskulatur kontrahiert und wann nicht. Und hier kommt eine weitere charakterisierende Eigenschaft ins Spiel, welche jede Art von Muskulatur gemeinsam hat, Muskulatur ist nämlich erregbar. Das bedeutet, dass ihre Membran ihren elektrischen Zustand ändern (von polarisiert zu depolarisiert) und eine elektrische Welle, die als Aktionspotential bezeichnet wird, über die Membran senden kann. Solch eine Erregung wiederum initiiert eine Kontraktion. Die Art und Weise, wie diese Erregung gesteuert wird, variiert aber zwischen den drei Typen von Muskulatur, was überhaupt erst der Grund dafür ist, dass man einen Skelettmuskel wie den Bizeps willentlich anspannen kann, glatte Muskulatur wie den Magen, oder die Herzmuskulatur allerdings nicht. Wie genau die Innervation (Steuerung) funktioniert, ist ein Thema, welches uns an diesen Punkt erstmal nicht weiter beschäftigen soll. So oder so, sobald Muskulatur erregt wird, kontrahiert sie. Diese Kontraktion wird genutzt, um zum Beispiel Nahrungsbrei im Darm vorwärtszubewegen, Blutgefäße zu verengen und so die Perfusion von Organen zu regulieren, Blut durch den Kreislauf zu pumpen, oder eben den Oberarm zu beugen, um ein Glas anzuheben. All das beruht auf der kontrollierten Zustandsregulierung von Muskulatur, welche entweder Spannung aufbaut oder eben entspannt. Bei der Kontraktion selbst ziehen sich die Muskelfasern, bzw. Muskelzellen in ihrer Längsachse zusammen, was äußerlich betrachtet zum Beispiel beim Biceps brachii sogar sehr gut beobachtet werden kann. Dieses „Zusammenziehen“ kommt durch spezielle kontraktile Filamente im Inneren der Muskulatur zustande, welche im Falle einer Erregung aktiviert werden und durch ihre Interaktion ineinandergleiten, was dann auf makroskopischer Ebene den Muskel verkürzen lässt.

In diesem Sinne wurde in vorherigen Abschnitten bei Betrachtung des Skelettmuskelsystems und dessen Funktionen vorwiegend von „Kontraktion“ bzw. „verkürzen“ oder auch „zusammenziehen“ von Muskeln gesprochen, was, wenn ein Muskel an beiden Enden an einem Teil des Skeletts fixiert ist und ein Gelenk überspannt, eine Bewegung auslöst. „Zusammenziehen“ bedeutet hier schlichtweg Kraftproduktion. Der Muskel „zieht sich zusammen“ und zieht damit zugleich am Knochen, an dem er befestigt ist, dieser Zug ist nichts anderes als Kraft. Und ebenso wie im vorher erwähnten Fall des Glases, das bewegt wird, wenn einwirkende Kräfte eine Bewegung auslösen, gilt das auch für das Skelett. Das Skelett entspricht im überwiegenden Teil schlichtweg einer Ansammlung an Knochen. Mechanisch betrachtet verhält sich so ein Knochen erstmal gleich wie das Glas (und alle anderen Körper), wenn keine Kräfte für Bewegung sorgen, bewegt er sich auch nicht.

Die Skelettmuskeln aber sind an Knochen befestigt und üben durch ihre Kontraktion Zugkraft auf die Knochen aus. Um das zu erreichen, müssen Muskeln entweder direkt oder indirekt am Knochen ansetzen. Das Bindegewebe, welches einen Muskel umhüllt (Epimysium) kann direkt an Knochen oder Knorpel ansetzen und so eine direkte Verbindung bilden. Eine indirekte Befestigung entsteht, wenn die Bindegewebsschichten (Epimysium, Perimysium und Endomysium) am Ende des Muskels einen Komplex bilden. Auf diese Weise sind Muskeln über Sehnen oder eine breitere Bindegewebsschicht, die als Aponeurosen bezeichnet werden, an Knochen (und anderen Muskeln) befestigt. Wenn sich ein Muskel also zusammenzieht, wird die Kontraktionskraft über den Ansatz übertragen, der am Knochen zieht, um eine Skelettbewegung hervorzurufen. Und auch hier bestimmt die Richtung, in welche diese Kraft ausgeübt wird, die Richtung in die der Knochen gezogen und damit welche Bewegung letztlich ausgelöst wird. Die Richtung wiederum, in welche ein Muskel zieht, ist in der Regel in Richtung seines Ursprungs (bzw. vom beweglichen knöchernen Glied, hin zum fixierten).

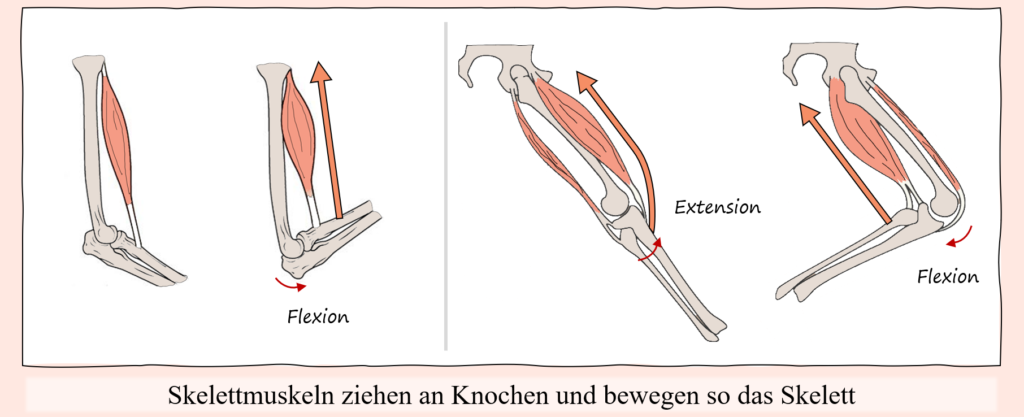
Diese simple Betrachtungsweise des Bewegungsapparates, mit dem Gedanken im Hinterkopf – „von wo bis wo verläuft Muskel X und was passiert, wenn man am Ansatz in Richtung Ursprung zieht“ – reicht schon aus, um ein grundlegendes anatomisches Verständnis für Bewegungen zu entwickeln. Zum Beispiel kann man allein damit bereits grob schlussfolgern, welche Muskeln bei einer beliebigen Bewegung beteiligt sind, wozu wir uns gleich auch ein paar Beispiele ansehen. Und im Umkehrschluss kann man daraus dann ebenso schließen, welche Bewegungen man ausführen könnte, um bestimmte Muskeln gezielt zu trainieren. Denn einen Muskel zu „trainieren“, bedeutet erstmal schlichtweg ihn zu beanspruchen, was wiederum bedeutet, eine Bewegung auszuführen, bei der jener Muskel beteiligt ist (als Agonist).

Eine relativ gängige Fragestellung im Trainingskontext beläuft sich so zum Beispiel auf die unterschiedliche Involvierung der Hüftmuskulatur bei unterschiedlicher Standbreite in einer Kniebeuge. In aller Regel geht es hier, vor allem um die großen (äußeren) Hüftmuskeln, und dadurch, dass sich eine Bewegung wie die Kniebeuge in Sachen Hüfte vor allem um die Extension dreht, um Muskeln, welche die Hüfte strecken. Das heißt, es geht um die Gluteus-Gruppe und auch der Adduktor Magnus, welcher ebenso als Hüftstrecker zählt, sollte miteinbezogen werden. Vielleicht erscheint es dem ein oder anderen zunächst recht schwierig anhand einer variierenden Standbreite zu schlussfolgern, welche Hüftmuskeln für die Bewegung verantwortlich sind, gerade weil das Hüftgelenk nun mal mehrere Bewegungsachsen aufweist und demnach ringsum von Muskeln umgeben ist. Unterm Strich bleibt das Prinzip aber dasselbe und genauso wie man weiß, dass der Bizeps dafür zuständig ist, den Ellbogen zu beugen und der Trizeps ihn zu strecken, kann man auch grob nachvollziehen, welche Hüftmuskeln bei einer gegebenen Hüftbewegung vorwiegend beteiligt sind. Hierzu muss man den Bewegungspfad des Oberschenkelknochens betrachten bzw. sich vorstellen. Also, wo bewegt sich der Oberschenkel hin und welche Muskeln ziehen ihn in diese Richtung. In der Grafik unten sind durch die transversale Betrachtung die groben Zug-Richtungen der jeweiligen Muskeln gekennzeichnet (In diesem Fall bietet sich diese Betrachtungsweise also recht gut an). Alle Muskeln entspringen an bestimmten Stellen am Becken und setzen am Oberschenkelknochen an, welchen sie dadurch umkreisen. Wohingegen der Adduktor Magnus, als Zugehöriger der Adduktoren, an der Innenseite des Oberschenkels verläuft, laufen die kleinen Gluteus-Muskeln eher auf der Seite und der große Gluteus Maximus auf der Rückseite. Bei Kontraktion ziehen sich die jeweiligen Muskeln zusammen und ziehen den Oberschenkel in Richtung ihres Ursprungs. Mit dieser Vorstellung im Hinterkopf betrachtet man nun die Bewegungsrichtung des Oberschenkels beim wieder Aufstehen (bei einer Kniebeuge findet zwar auch eine Hüftflexion statt, wenn man nach unten geht, dadurch dass die Schwerkraft aber nach unten zieht, geht es hierbei aus Hinsicht der muskulären Belastung nicht um eine aktive Hüftflexion, sondern um ein „Abbremsen“, also um eine über die Extensoren kontrollierte Flexion.) Beim schmalen Stand werden die Oberschenkel erst relativ gerade nach vorne gebeugt und beim wieder Aufstehen wieder zurückgeführt. Beim breiten Stand werden die Oberschenkel im Gegenzug nach lateral bewegt und müssen im Zuge des wieder Aufstehens wieder zurückgeführt werden. Vergleicht man jene Bewegungsrichtungen mit den Zugbereichen der jeweiligen Muskeln wird ersichtlich, dass der schmale Stand vorwiegend in den Bereich des Gluteus Maximus fällt und beim breiten Stand zum Maximus noch vermehrt der Adduktor Magnus hinzukommt. Was die kleinen Gluteus-Muskeln angeht, so sind sie ihrer stabilisierenden und Extensions-unterstützenden Rolle wegen natürlich auch beteiligt, jedoch würden sie gemäß ihrer Zugrichtung die Oberschenkel, seitlich nach hinten Abspreizen und passen damit nicht direkt in die Agonisten-Rolle jener Bewegungen.

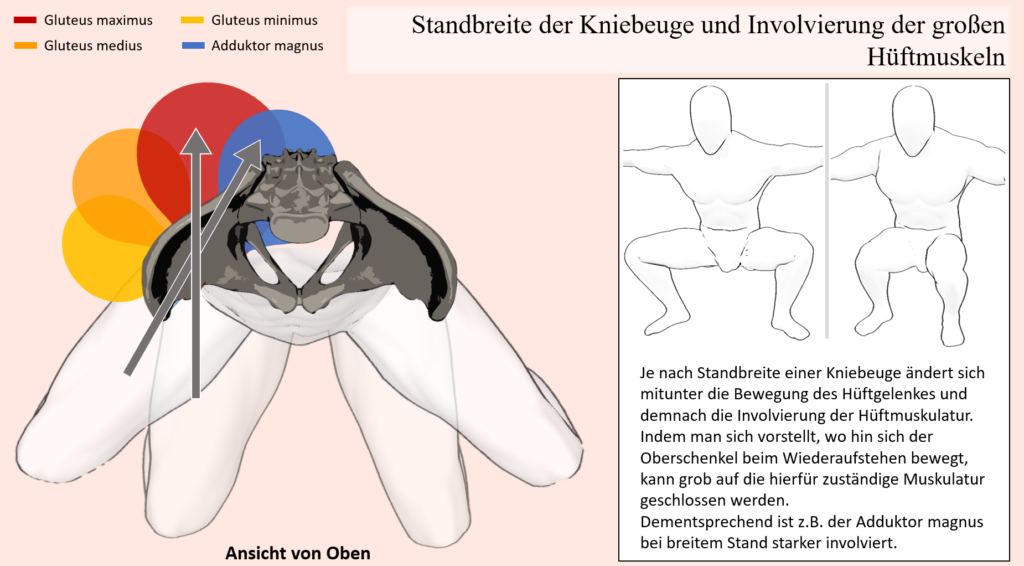
Um nun tatsächlich auf das Ausmaß der jeweiligen muskulären Belastung beteiligter Muskeln zu schließen, reicht diese anatomische Betrachtung der Hüfte nicht ganz aus, vor allem wenn es um eine Kniebeuge geht, wo nicht nur das Hüftgelenk bewegt wird. Hierbei geht es dann vielmehr um eine zusätzliche Betrachtung der Hebelverhältnisse der Bewegung an sich und der jeweiligen Muskeln, und wie diese sich im Laufe der Bewegung verändern. Für uns ist das an diesem Punkt aber erstmal sekundär, schließlich geht es hier um das funktionelle anatomische Verständnis der Skelettmuskulatur, also erstmal zu verstehen welche Muskeln bei einer Bewegung beteiligt sind, bzw. welche Bewegungen bestimmte Muskeln verursachen und nicht in welcher mechanischen Position sich entsprechende Muskeln im Laufe dieser Bewegungen befinden.

Sehen wir uns hierzu also einige weitere Beispiele an.

Nehmen wir zum Beispiel mal an, man möchte den Deltoid pars posterior, also die hintere Schulter, sowie die horizontalen Trapezius- und Rhomboid-Fasern trainieren, dann bedeutet das, dass man eine Bewegung ausführt, welche die Bewegungsfunktion entsprechender Muskeln möglichst gut abdeckt. Das bedeutet, um die Bewegungsfunktion der horizontalen Trapezius- und Rhomboid-Fasern zu erfüllen, dreht sich die Bewegung um die Schulterblattbewegung, wohingegen für die Bewegungsfunktion der hinteren Schulter die Bewegung im Glenohumeralgelenk (Schultergelenk) im Fokus liegt, was sich auch in der jeweiligen Trainingsübung typischerweise widerspiegelt.

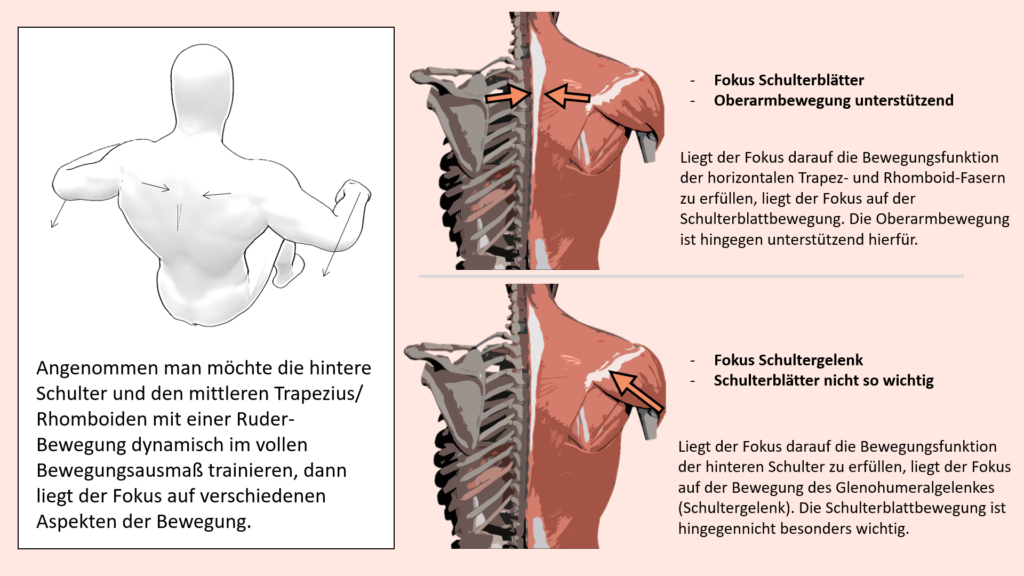
Ein weiteres gutes Beispiel, um die funktionelle Rolle der Skelettmuskulatur zu verstehen, sind verschiedene Bewegungsfunktionen von verschiedenen Teilen desselben Muskels. Mit dem Gedanken im Hinterkopf, dass Muskeln sich in einer Richtung zusammenziehen, können breitgefächerte Muskeln wie zum Beispiel der Latissimus dorsi in verschiedene Anteile separiert werden, welche je nach Verlauf mehr oder weniger verschiedene Bewegungen auslösen. Im Falle des Latissimus kann man ganz grob zwischen vertikalen sowie horizontalen Fasern unterscheiden, wobei der Ansatz am Oberarmknochen derselbe ist, der Ursprung und damit die Verlaufsrichtung sich aber recht stark unterscheidet. Wohingegen die vertikalen Fasern nach unten Richtung Becken und Lendenwirbelsäule ziehen, ziehen die oberen, horizontalen Fasern in Richtung Brustwirbelsäule.

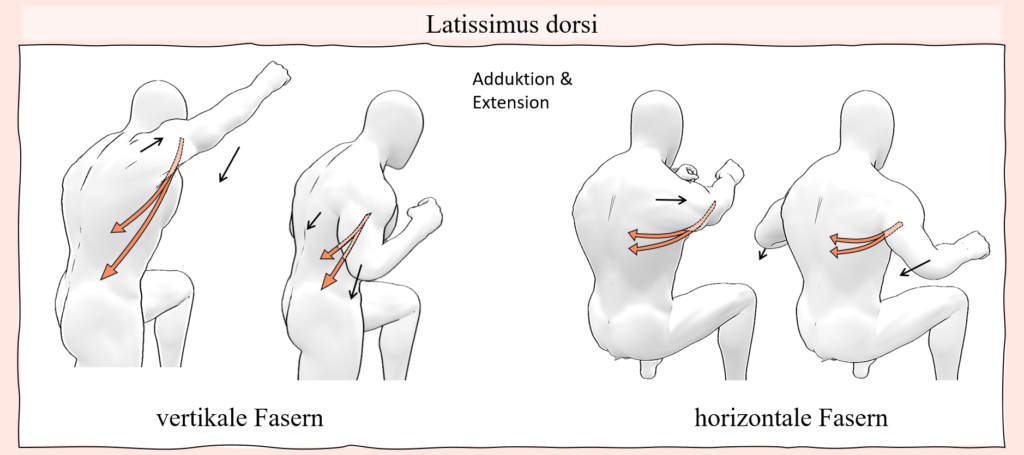
Hier kommen wir zugleich auch zu einer kleinen Besonderheit, was den Schultergürtel angeht. Normalerweise zieht ein Muskel von seinem Ursprung zum Ansatz und überzieht dabei in der Regel mindestens ein Gelenk. Das gilt natürlich auch für den Schultergürtel und den Muskeln des Schultergürtels. Dadurch, dass der Schultergürtel aber ein beweglicher Komplex ist, funktionieren auch Muskeln wie zum Beispiel der Latissimus dorsi oder Pectoralis major quasi als mehrgelenkige Muskeln, die nicht nur über das Glenohumeralgelenk ziehen, sondern dadurch ebenso den restlichen Schultergürtel beeinflussen, indem sie die Schulterblätter mitbewegen. Im Umkehrschluss bedeutet das auch, wenn man nun einen Muskel wie den Latissimus oder aber den Pectoralis major in ihrem vollen Bewegungsausmaß trainieren möchte, dass nicht nur die jeweilige Bewegung des Schultergelenkes selbst (Glenohumeralgelenk), sondern eben auch die Schulterblätter miteinbezogen werden müssen. Zu erkennen ist dies sowohl in der obigen Darstellung als auch in der Grafik unten, wo der Arm zwar nach oben angehoben ist, die Schulterblätter aber in depressiver Stellung verharren und dadurch nicht das volle Bewegungsausmaß erreicht werden kann.

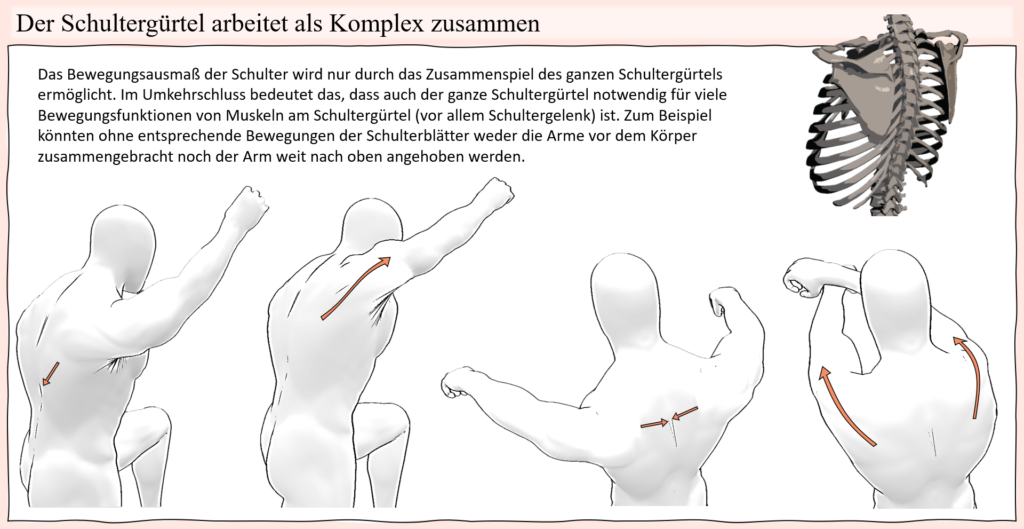
Wir sehen also durch dieses einfache Verständnis von Muskelzugrichtung und Ansatzpunkt kommt man schon recht weit.

Trotzdem reicht das aber noch nicht ganz aus, um die Bewegungen des menschlichen Bewegungsapparates weitreichend zu verstehen, denn hierfür müssen die Gelenke, oder vielmehr die Bewegungsachsen der Gelenke weiter miteinbezogen werden. Gelenke bilden Drehpunkte zwischen den steifen Knochen und schaffen bewegliche Verbindungen zwischen diesen. Das wiederum hat zur Folge, dass wenn ein Muskel an einem Knochen zieht, an dem er befestigt ist, dieser Knochen sich nicht gleich verhält wie das frei stehende Glas. Vielmehr steht der Knochen über bewegliche Gelenke in Verbindung mit dem restlichen Skelett. Wird also an dem steifen Knochen gezogen, so resultiert dies in einer Gelenkbewegung. So weit, so gut, das hatten wir ja schon. Das Skelett und die Muskeln wirken also zusammen, um den Körper zu bewegen. An dieser Stelle wird es aber notwendig, oder vielmehr ist es hilfreich sich das Funktionsprinzip dahinter etwas genauer anzusehen. Und zwar wird das Funktionsprinzip, das beim Zusammenspiel von Skelettmuskeln und Skelett zum Tragen kommt, von den Hebelgesetzen beschrieben. Das bedeutet man kann anhand von Beschreibungen, die auf Hebeln basieren erklären, bzw. verstehen wie Muskeln auf Knochen und das Skelett einwirken. Auch das ist relativ simpel. Man stelle sich vor, man entfernt mit der Klaue eines Zimmermannshammers einen Nagel aus einem Stück Holz. Der Griff fungiert als Hebel und der Kopf des Hammers als Drehpunkt, also der feste Punkt, auf den die Kraft ausgeübt wird, wenn man den Griff zurückzieht oder nach unten drückt. Der Kraftaufwand in diesem Beispiel besteht darin, am Griff zu ziehen oder zu drücken, um den Nagel zu entfernen, was wiederum der Last bzw. dem „Widerstand“ gegen die Bewegung des Griffes entspricht. Unser Bewegungsapparat funktioniert auf ähnliche Weise, wobei die Knochen steife Hebel sind und die Gelenk-Enden der Knochen als Drehpunkte fungieren. Die Last wäre ein angehobener Gegenstand oder ein Widerstand gegen eine Bewegung (z.B. ist der Kopf eine Last, wenn man ihn anhebt, bzw. bewegt), und die Anstrengung oder ausgeübte Kraft entsteht durch die Kontraktion der Skelettmuskulatur. Die Kraft, welche von den Muskeln erzeugt und auf den Knochen ausgeübt wird, erzeugt ein sogenanntes Drehmoment im Gelenk. Als Drehmoment beschreibt man schlichtweg Kräfte, welche Rotationsbewegungen auslösen, also in diesem Falle das Gelenk rotieren lassen (z.B. Flexion/Extension).

Ein Hebel ist also eine starre Struktur, in diesem Fall ein Knochen, der sich um einen festen Punkt, dem Drehpunkt, in diesem Fall einem Gelenk, bewegt. Im Körper sind die meisten Knochen Hebel und die (synovialen) Gelenke Drehpunkte, und Muskeln sorgen für die Kräfte, welche diese kontrolliert bewegen.

Auf diese Weise kontrollieren Muskeln die Gelenke. Wichtig zu beachten sind natürlich die Bewegungsmöglichkeiten, welche entsprechende Gelenke überhaupt erlauben, weil dies den Bewegungsrahmen vorgibt. Letztlich sind Muskeln entsprechend ihrer Funktion angeordnet und stehen in funktioneller Verbindung mit den Gelenken, soll heißen für alle Bewegungen, zu welchen ein Gelenk in der Lage ist, gibt es Muskeln, welche diese Bewegung ausführen. Welche Bewegung ein Muskel erzeugt, hängt vom Ansatzort und der Zugrichtung im Verhältnis zum Drehpunkt ab. Geht es zum Beispiel um ein Scharniergelenk wie den Ellbogen, so ist das Gelenk (Humeroulnargelenk) zur Flexion- und Extension in der Lage. Ob ein Muskel, der über das Ellbogengelenk nun zur Flexion oder Extension beiträgt, kommt auf jene beiden Faktoren an, den Ansatzpunkt und der Zugrichtung im Verhältnis zum Gelenk.

In diesem Fall können wir den Drehpunkt also als eine Flexions-/ Extensionsachse betrachten, anhand derer zwischen Flexoren und Extensoren unterschieden werden kann. Die in der unten angeführten Darstellung aufgezeigte Strichlinie gibt die Trennlinie zwischen Extension und Flexion vor. Würde ein Muskel genau in Richtung dieser strichlierten Linie ziehen, würde er weder eine Flexion noch Extension auslösen. Das hat damit zu tun, dass in diesem Falle die Kraftrichtung des Muskels direkt durch den Drehpunkt läuft, keinen Hebelarm hat und im Umkehrschluss kein Drehmoment im Gelenk erzeugt (Drehmoment=Kraft*Hebelarm) und dieses demnach auch nicht zur Flexion oder Extension verleitet. Für unsere Zwecke in diesem anatomischen Kontext ersparen wir uns aber erstmal die weitere Inbezugnahme von Hebelarmen. Dies wird wie gesagt notwendig, um zu verstehen, weshalb ein Muskel zum Beispiel in unterschiedlichen Gelenkpositionen stärker zu bestimmten Gelenkbewegungen beitragen kann, wenn es aber lediglich um das anatomische Verständnis darüber geht, welche Bewegung entsteht, wenn ein Muskel kontrahiert, dann reicht erstmal die intuitivere, wenn auch nicht ganz exakte Vorstellung von: „in welche Richtung wird die Achse-A gedreht, wenn man an Stelle-X am Knochen in Richtung-Y zieht“. Denn auch mit dieser simplen Fragestellung sollte man erkennen, dass der Zug in Richtung der strichlierten Linie in der Grafik unten, die Flexions-/ Extensionsachse in keine Richtung dreht. Zieht ein Muskel hingegen über oder unter diese Strichlinie hinweg (und verläuft über das Ellbogengelenk), beugt oder streckt er den Ellbogen durch seine Kontraktion. So verlaufen die Zugrichtungen von Biceps brachii und Triceps brachii auf entgegengesetzter Seite der Flexions-/Extensionsachse, weswegen der Trizeps zur Extension und der Bizeps zur Flexion beiträgt.

Selbstverständlich ist gerade dieses Beispiel mit Bizeps/Trizeps recht simpel und man bedarf sich wohl keine Flexions-/ Extensionsachse vorzustellen, um zu verstehen, dass der Trizeps den Ellbogen streckt und der Bizeps ihn beugt, wenn man sich schlichtweg vorstellt, was passiert, wenn man am Ansatz des Bizeps/ Ansatz des Trizeps am Knochen zieht. Aber gerade bei Gelenken mit mehr Bewegungsmöglichkeiten, wie dem Schulter- oder Hüftgelenk ist es hilfreich auf solche Achsen bewusst zu achten, um zum Beispiel zu verstehen, weshalb kaudale Fasern des Gluteus Maximus zur Adduktion und kraniale Fasern zur Abduktion beitragen und wie sich dies je nach Ausgangsposition ändern kann.

Wie dem auch sei, im Folgenden werden wir uns einige ausgewählte Beispiele am Hüft- und Schultergelenk ansehen, welche die jeweiligen Bewegungsachsen aufgreifen und unter anderem auch zeigen, wann und warum einige Muskeln je nach Gelenkposition ihre Bewegungsfunktion ändern können.

Das Hüftgelenk ist ein Kugelgelenk und weist damit drei Bewegungsachsen auf, die wiederum je zwei, in Summe also 6, Bewegungsrichtungen erlauben. Sowohl Innen und Außenrotation, Abduktion und Adduktion als auch Flexion sowie Extension sind möglich. In der Grafik unten sind diese Achsen getrennt voneinander dargestellt, wobei diese in Realität natürlich im Kugelgelenk alle zusammengefasst sind. Bei Betrachtung einzelner Muskeln und Bewegungen kann es aber hilfreich sein, diese Achsen separiert im Hinterkopf zu halten.

Je nachdem, wie die Kraftlinie des Muskels in Bezug auf diese Achsen verläuft, bzw. wo genau am beweglichen Glied der Muskel ansetzt und hinzieht, ergibt sich bei Kontraktion eine spezifische Bewegung. Dadurch, dass sowohl der Ursprung als auch der Ansatz aber definierte Bereiche an bestimmten Knochen sind, sich im Laufe der Bewegung also nicht ändern, sondern vielmehr die Lage der Knochen relativ zueinander verändert wird, bringt eine Gelenkbewegung zwangsweise einen veränderten Verlauf der Kraftlinie mit sich.

Das ist zum Beispiel der Grund, weshalb der Gluteus Maximus bei zunehmende Hüftflexion ein „schwächerer“ Extensor wird, weil sein Hebelarm abnimmt, aber auch, dass in gebeugter Position seine zweigeteilte Rolle als Adduktor und Abduktor in Richtung der Abduktion verschoben wird. Je nach anatomischer Lage des Muskels sowie des Ausmaßes der jeweiligen Bewegung können solche Veränderungen stärker oder schwächer ausfallen. In einigen Beispielen fallen sie so groß aus, dass sich sogar die Muskelfunktion umkehren kann.

Wie auch im obigen Beispiel kann man sich hier also eine „0-Linie“ für entsprechende Achsen vorstellen, denn dies ist der Bereich, an dem sich die jeweiligen Bewegungsrichtungen der entsprechenden Achse kreuzen (z.B. Extension/Flexion). Auf welcher Seite dieser „0-Linie“ die Zugrichtung eines Muskels nun verläuft, entscheidet darüber, in welche Richtung der Knochen gezogen und damit welche Bewegung ausgelöst wird. Wechselt der Muskel, oder ein Teil des Muskels nun in bestimmten Gelenkpositionen die Seite, wechselt auch seine Bewegungsfunktion.

Ein gutes Beispiel können hierbei die Adduktoren sein. Um genauer zu sein, ein Vergleich des Adduktor Magnus und Adduktor longus/brevis. Der Adduktor longus und Adduktor brevis fungieren neben ihrer namensgebenden Rolle als Adduktoren meistens (nahe an der Normalposition) als Flexoren, das heißt, sie beugen das Hüftgelenk. Der Adduktor Magnus hingegen unterstützt neben der Adduktion vielmehr die Extension, also Streckung der Hüfte. Grund hierfür ist der Ursprung am Sitzbein des Adduktor Magnus, wohingegen die Adduktoren longus und brevis am Schambein entspringen. Betrachtet man den jeweiligen Muskelverlauf aus sagittaler Perspektive mitsamt der Flexions-/ Extensionsachse und der gedachten 0-Linie, dann wird ersichtlich, dass die Adduktoren Magnus und longus/brevis den Oberschenkel (in der Normalposition bzw. leichter Flexion) in die jeweils andere Richtung ziehen, wodurch der Adduktor Magnus die Extension und die Adduktoren longus und brevis die Flexion unterstützen. So weit, so gut, verändert man nun aber die Gelenksposition mit einer zunehmenden Flexion des Hüftgelenkes, dann wird man feststellen, dass die Zuglinie der Adduktoren longus und brevis die Flexions-/ Extensionsachse überschreiten und nun wie auch der Adduktor Magnus die Extension unterstützen. Der Adduktor Magnus hingegen bleibt bei zunehmender Hüftflexion ein Extensor, bzw. gewinnt hier sogar maßgeblich an Beteiligung. Bei einer „Überstreckung“ der Hüfte, also einer Hüftstreckung über die 0-Position hinaus, kann der Adduktor magnus dann auch geringfügig zur Flexion beitragen (in der Grafik unten nur im Diagramm dargestellt), jedoch ist dies sehr beschränkt, weil die Extension des Hüftgelenkes ausgehend von der 0-Position im Gegensatz zur Flexion sehr limitiert ist.

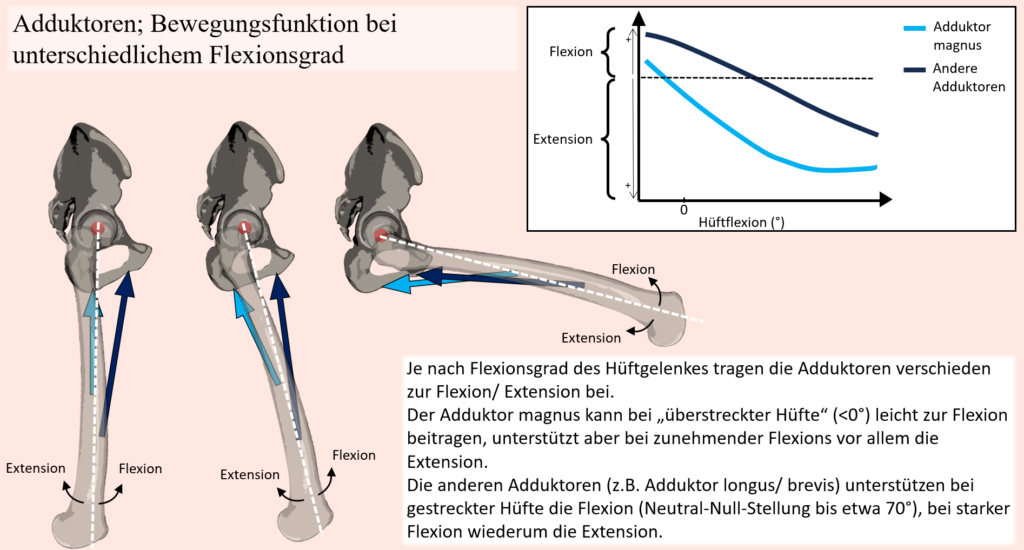
Das ist ein klassisches Beispiel für eine Umkehrung der Bewegungsfunktion eines Muskels bei unterschiedlichen Gelenkpositionen.

Ein weiteres gut ersichtliches Beispiel hierfür bietet uns die Betrachtung der Rolle des Gluteus medius hinsichtlich der Außen- bzw. Innenrotation des Femurs. Dabei fungiert der Muskel bei geringen Flexionsgraden als Außenrotator (gut zu erkennen in der Darstellung unten ganz rechts), bei zunehmender Flexion des Hüftgelenkes wird aber auch hier die Zugrichtung des Muskels im Verhältnis zur Achse verlagert und er trägt vermehrt zur Innenrotation bei (Darstellung in der Mitte, rechte Seite). Was den Gluteus Maximus angeht, wird durch die Darstellung ganz links ersichtlich, dass kranial (oberhalb) und kaudal (unterhalb) verlaufende Fasern je zur Abduktion oder aber Adduktion beitragen, weil sie nun mal auf verschiedenen Seiten der Adduktion-/ Abduktionsachse verlaufen und somit den Oberschenkel abduzieren, also abspreizen oder aber adduzieren (anziehen). Wird die Hüfte gebeugt, so beschreibt Adduktion/ Abduktion vielmehr eine horizontale Auswärts-/ Einwärtsdrehung, wobei eine Betrachtung aus transversaler Perspektive wohl besser geeignet wäre als die Frontalebene, welche hier dargestellt ist (was aber aus Platzgründen nicht separat dargestellt wird). Dadurch dass der Gluteus auf der Hinterseite des Beckens und aus transversaler Sicht damit posterior (hinter) der Achse verläuft, trägter bei gebeugter Hüfte vermehrt zu Abduktion bei, wohingegen die Adduktoren auf der anderen Seite, also anterior zur Achse verlaufen und damit auch in dieser Position die Oberschenkel vorne zusammenbringen ((horizontale) Adduktion).

Kommen wir nun also zum Schultergelenk. Wie auch beim Hüftgelenk handelt es sich hierbei um ein Kugelgelenk, das heißt es besitzt dieselben Bewegungsachsen, also eine Flexions-/ Extensionsachse, eine Adduktion-/ Abduktionsachse als auch eine Innenrotation-/ Außenrotationsachse. Und wie auch das Hüftgelenk wird auch die Schulter ringsum von Muskeln umgeben, die den Oberarmknochen in alle möglichen Richtungen bewegen, wobei das Bewegungsausmaß wegen der beträchtlich kleineren Gelenkpfanne höher ausfällt, das heißt die Achsen können weiter in entsprechende Richtungen gedreht werden.

Und auch wie im Falle einiger oben erwähnter Beispiele von Hüftmuskeln wechseln auch hier die Bewegungsfunktionen einiger Muskeln bei unterschiedlichen Gelenkpositionen. Beispiele hierfür sind die posterioren sowie anterioren Anteile des Deltoids, die superioren, also klavikularen Brustfaseranteile, als auch Muskeln der Rotatorenmanschette, wie z.B. der subscapularis und der infraspinatus. Sie wirkten nämlich je nach Gelenkwinkelposition im Glenohumeralgelenk, entweder bevorzugt abduzierend oder aber adduzierend. Die Ursache hierfür ist dieselbe wie auch bei den obigen Beispielen am Hüftgelenk. Wenn sich durch die Gelenkbewegung das Verhältnis der Zugrichtung des Muskels (oder Muskelanteils) zum Gelenk verändert und die Bewegungsachsen überwandert werden, dann sorgt eine Kontraktion entsprechender Muskeln bzw. anatomischen Subgruppen für unterschiedliche Bewegungen.

Der Deltoid-Muskel setzt sich aus drei Teilen zusammen, den Pars clavicularis oder der vorderen Schulter, den Pars acromialis oder der seitlichen Schulter und den Pars spinalis oder der hinteren Schulter. Die Funktionen der drei Anteile hängen von der Lage zur Bewegungsachse und der Stellung des Humerus ab. Die einzelnen Anteile wirken dabei sowohl antagonistisch als auch synergistisch. Bei einer Abduktion von weniger als 60° wirken die vordere und hintere Schulter der Abduktion durch die seitliche Schulter entgegen, verhalten sich also antagonistisch und unterstützen die Adduktion. Bei einer Abduktion von mehr als 60° unterstützen sie hingegen die Abduktion und fungieren synergistisch zur seitlichen Schulter. Aus der Neutral-Null-Stellung abduziert die seitliche Schulter (Pars acromialis) den Arm und sichert jede neu eingenommene Stellung. Bei zunehmender Abspreizung (etwa ab 60°) beteiligen sich auch die klavikularen und spinalen Anteile an der Abduktion, weil sie die Abduktions-/Adduktionsachse überwandern und somit ihre Funktion ändern.

Das Glenohumeralgelenk ist des Weiteren ein gutes Beispiel, um aufzuzeigen, inwiefern der Gelenkkaufbau und dadurch vorgegebene Bewegungsmöglichkeiten die Stellung und Funktion anzutreffender Muskulatur beeinflussen können.

In diesem Bezug wird es also wichtig, anatomische Beschaffenheiten und ihre potenziellen Auswirkungen auf eine Bewegung miteinbeziehen zu können. Zum Beispiel bei einer Abduktion des Armes (seitliches Anheben), dann kann dies nur bis zu einem gewissen Punkt (ca. 90 Grad) mit einer Innenrotation des Humerus ausgeführt werden. Wird dieser Gelenkwinkel überschritten, führt das zu einer unwillkürlichen, also nicht zu unterbindenden (insofern der Arm weiter gehoben wird), Außenrotation. Dies ist auf den großen Humerushöcker, bzw. seine „Kollision“ mit dem Schulterdach, bei innen rotierter Humerusstellung zurückzuführen. Im funktionellen Aspekt heißt das nun allerdings auch, dass sich die Rotationsstellung des Humerus ändert und mit ihr auch die Stellung spezifischer Faserbereiche hin zum Drehpunkt des Gelenkes. Damit kann eine solche Abduktion ab ca. 90 Grad nicht nur die notwendige Involvierung anderer Muskeln, (wie bspw. dem Trapez, der für die Rotation des Schulterblattes wichtig wird) beeinflussen, sondern auch die Involvierung unterschiedlicher Faserbereiche des Deltoideus in der Bewegung (bspw. verbesserte Verhältnisse der vorderen Schulterfaseranteile für die Abduktion).

Der Pectoralis major, also der große Brustmuskel, ist ein großer fächerartiger Muskel, der fast den ganzen Brustbereich abdeckt. Sein Ursprung geht vom Schlüsselbein, über das Brustbein bis hin zu den oberen Rippenknorpeln. Anhand dieser unterschiedlichen Ursprünge unterscheidet man auch zwischen den drei Teilen, den Pars clavicularis oder der oberen Brust, den pars sternocostalis oder der mittleren Brust, sowie den pars abdominalis oder der unteren Brust. Alle Teile verlaufen hin zum Oberarmknochen zusammen, was bedeutet, dass die Kraftrichtung und damit die Richtung, in welche sie den Oberarm bei Kontraktion ziehen, variiert. In der anatomischen Normalposition, also wenn die Arme seitlich am Körper anliegen, führt eine Kontraktion des pectoralis major einheitlich zu einer Adduktion und Innenrotation des Armes. Ist der Arm seitlich angehoben (Abduktion), dann sorgt die Kontraktion des Pectoralis major einheitlich für die horizontale Adduktion, weswegen er auch der wichtigste Agonist für eine Liegestütze-Bewegung ist. Hinzu kommt die Zugrichtung der oberen Fasern nach schräg oben zum Schlüsselbein, was dazu führt, dass der obere Brustanteil aus der Normalposition heraus auch die Flexion unterstützt, wohingegen die mittleren und unteren Anteile bei angehobenen Arm wiederum die Extension unterstützen können. Bei sehr starker Schulterflexion (Arm bis hinter die Schulter angehoben) unterstützt schließlich auch der obere Anteil geringfügig die Extension der Schulter. Wo aber der Funktionswechsel am besten ersichtlich ist, ist die besagte Adduktion/ Abduktion, denn wohingegen der Pars clavicularis aus der 0-Position heraus zur Adduktion beiträgt, überwandern die Fasern im Laufe der Adduktion teilweise die Adduktion-/ Abduktionsachse und unterstützen folglich weiterhin die Abduktion.

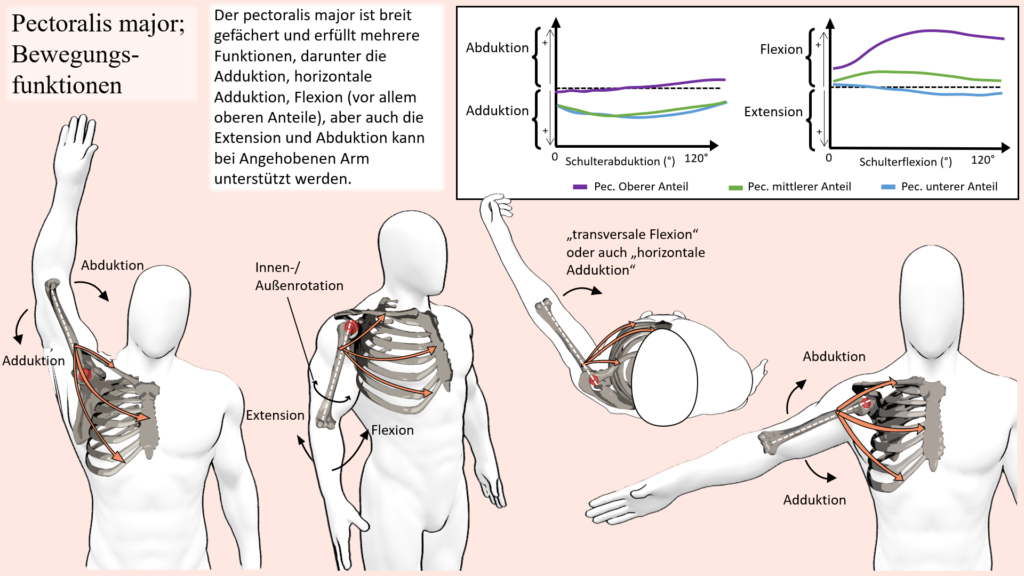
Ein weiteres Beispiel der Bewegungsfunktion von Muskeln am Glenohumeralgelenk ist die Rotatorenmanschette, welche sich aus vier einzelnen Muskeln zusammensetzt und das Schultergelenk wie eine Manschette umschließt. Betrachtet man die Zurichtungen der einzelnen Muskeln, dann kann man auch hier gewisse Unterschiede je nach Gelenkposition, bzw. Muskelanteilen feststellen. Mit der Funktion als stabilisierende Manschette, welche das Gelenk umspannt, und in Anbetracht, dass besonders der Subscapularis und Infraspinatus relativ großflächig sind, ist es recht ersichtlich, dass die jeweils untersten und obersten Muskelanteile kleinere funktionelle Unterschiede mit sich bringen. Der infraspinatus gilt erstmal vorwiegend als Außenrotator, wobei die superioren Faseranteile zusätzlich bei abduzierten Arm aber eher den Supraspinatus, also die Abduktion unterstützen und die inferioren Fasern mit dem Teres minor zusammen vermehrt zur Adduktion beitragen. Der Subscapularis hingegen gilt vor allem als Innenrotator und unterstützt die Adduktion, wobei gerade die superioren Anteile zumindest auch die Abduktion leicht unterstützen können.

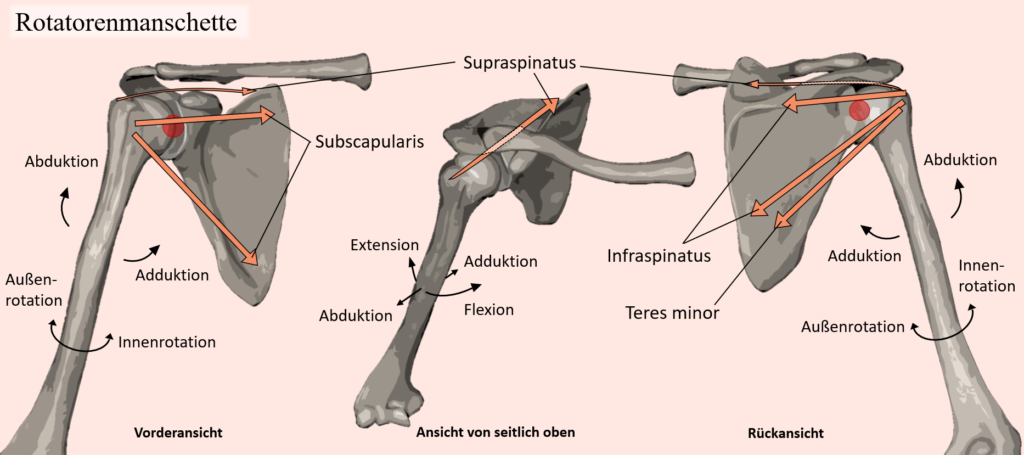
Solche „Funktionswechsel“ gelten aber natürlich nicht für alle Muskeln, sondern zunächst vor allem für Muskeln am Schulter- und Hüftgelenk, wegen der großen Bewegungsvielfallt. Und selbst hier gilt dies nicht für alle ansässigen Muskeln. So bleibt zum Beispiel der Latissimus seiner Bewegungsfunktion im Wesentlichen treu, auch wenn sein relativer Beitrag je nach Gelenkposition variieren kann (aber das ist wieder eine Frage des Hebelarms, den der Muskel auf das Gelenk ausübt).

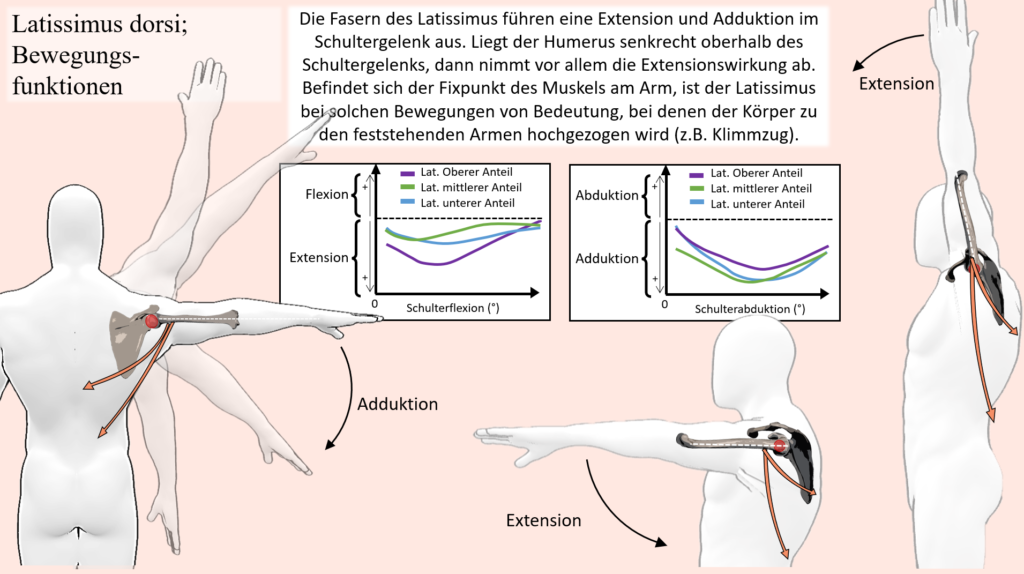
Zusammenfassend kann man also festhalten, dass man durch das anatomische Hintergrundwissen zum Verlauf (Ursprung und Ansatz) eines Muskels, den grundlegenden Aufbau der Gelenke, welche von den Muskeln überzogen werden, und der Inbezugnahme daraus resultierender Bewegungsachsen der Gelenke sowie Zugrichtungen der Muskulatur auf die groben Bewegungsfunktionen entsprechender Muskeln schließen kann. „Grob“, oder zumindest nicht ganz genau, weil man natürlich nicht vergessen sollte, dass es immer einer gewissen Simplifizierung entspricht, wenn man einen ganzen Muskel auf eine, oder einige wenige Zugrichtungen herunterbricht. Doch für den praktischen Umgang reicht dieses Maß an Genauigkeit in aller Regel vollkommen aus.

Kniegelenk

Der